Выпрямители: основные виды сглаживающих фильтров и особенности их применения в выпрямителях

ВВЕДЕНИЕ

В наше время высоких технологий всё более распространёнными становятся нелинейные нагрузки (частотные преобразователи, инверторы, системы бесперебойного питания, импульсные источники питания, люминесцентные и светодиодные лампы и т.п.). Из-за таких изменений в структуре нагрузки основной темой в этом десятилетии стали качество электроэнергии и снижение уровня гармоник. Проблемы, вызываемые гармониками, такие как перегрев трансформаторов и вращающихся машин, перегрузка проводников нейтрали, выход из строя конденсаторных батарей и т.п., приводят к повышению эксплуатационных расходов и также могут привести к снижению качества продукции и производительности труда. Кроме того, изменения в структуре генерации электроэнергии в сторону использования энергии ветра и солнечных батарей, которые тоже генерируют гармоники, также приводят к тому, что применение фильтров гармоник становится всё более важным для обеспечения стабильного энергоснабжения с приемлемым качеством электроэнергии.

Снизить уровень гармоник можно с использованием пассивных фильтров (составленных из конденсаторов, реакторов и резисторов) или активных фильтров (генерирующих гармоники в противофазе к гармоникам искажений и за счёт этого их уничтожающих)

Хотя основные принципы работы активных фильтров были выработаны ещё в 1970-е годы, они стали привлекать к себе повышенное внимание в последние несколько лет, потому что появилась возможность использования биполярных транзисторов с изолированным затвором (IGBT) и цифровых сигнальных процессоров (ЦСП). При этом разница в стоимости между активными и пассивными фильтрами становится не такой большой, как в прошлом. В этой статье сравниваются преимущества и недостатки активных и пассивных технологий фильтрации

Рассматриваются пассивные и активные решения для снижения уровня гармоник и стабилизации сети, направленные на решение проблем, которые возникают в современных областях применения и имеют тенденцию к возникновению в будущем

В этой статье сравниваются преимущества и недостатки активных и пассивных технологий фильтрации. Рассматриваются пассивные и активные решения для снижения уровня гармоник и стабилизации сети, направленные на решение проблем, которые возникают в современных областях применения и имеют тенденцию к возникновению в будущем.

Определение частоты среза

Кривая на диаграмме Найквиста, конечно, не имеет типового спада характеристики, который мы хорошо знаем из графиков амплитудно-частотных характеристик, и фактически график Найквиста не дает нам конкретной информации о частоте среза схемы фильтра. Однако изучение взаимосвязи между частотой среза и кривой Найквиста является хорошим способом укрепить понимание концепции частоты среза в целом, а также даст нам некоторое представление об ограничениях подхода Найквиста для визуального изображения частотной характеристики.

Во-первых, нам нужно подумать о том, что на самом деле происходит на частоте среза, с точки зрения как амплитудно-частотной, так и фазо-частотной характеристики.

Частота среза относительно амплитуды

Вы, вероятно, знаете, что другое название для частоты среза – это «частота 3 дБ» (или –3 дБ), и это напоминает нам о том, что фильтр нижних частот первого порядка обеспечивает ослабление на 3 дБ (или, что эквивалентно, усилению –3 дБ), когда входная частота равна ω. Мы не используем децибелы на графике Найквиста, поэтому вместо –3 дБ мы используем соответствующий коэффициент передачи в разах, который равен \(\frac{1}{\sqrt{2}}\)

Когда мы работаем с графиком в полярной системе координат, мы всегда должны помнить о треугольниках; например, амплитуда (модуль) комплексного числа определяется как гипотенуза прямоугольного треугольника, два катета которого являются действительной и мнимой частями; а для вычисления фазы (угла) комплексного числа мы используем тригонометрические функции. Теперь, когда вы думаете с точки зрения треугольников, коэффициент \(\frac{1}{\sqrt{2}}\) дает вам какие-нибудь идеи?

Рисунок 2 – Прямоугольный треугольник. Длина катетов равна 1

Как показано выше, коэффициент \(\sqrt{2}\) вступает в игру всякий раз, когда у прямоугольного треугольника два катета равной длины. Если уменьшить длину катетов до 0,5, длина гипотенузы будет равна \(\sqrt{2} \times 0,5\), что то же самое, что \(\frac{1}{\sqrt{2}}\).

Рисунок 3 – Прямоугольный треугольник. Длина катетов равна 0,5

Итак, что же всё это значит? Рассмотрим следующий график Найквиста:

Рисунок 4 – Это график Найквиста для фильтра нижних частот первого порядка

Обратите внимание, что я не добавил часть графика, которая соответствует отрицательным частотам

Как видите, в самой нижней точке кривой коэффициент усиления фильтра равен \(\frac{1}{\sqrt{2}}\), где абсолютное значение действительной части равно абсолютному значению мнимой части; это и есть местоположение частоты среза на графике Найквиста для фильтра нижних частот первого порядка. То же самое отношение применяется к фильтру верхних частот первого порядка, за исключением того, что в этом случае частота среза находится в самой высокой точке кривой:

Рисунок 5 – Частота среза фильтра верхних частот первого порядка на диаграмме Найквиста

Разница заключается в том, что сдвиг фазы фильтра верхних частот с увеличением частоты изменяется от +90° до 0°, тогда как фаза фильтра нижних частот изменяется от 0° до –90°. Поскольку угол измеряется против часовой стрелки от положительной действительной оси, положительный сдвиг фазы отображается над действительной осью, а отрицательный сдвиг фазы отображается ниже действительной оси.

Также обратите внимание, что на этих двух графиках есть стрелки, указывающие в противоположных направлениях: на графике фильтра нижних частот стрелка указывает на начало координат, поскольку с увеличением частоты коэффициент усиления уменьшается; на графике фильтра верхних частот она указывает в сторону от начала координат, поскольку с увеличением частоты коэффициент усиления увеличивается

Частота среза относительно сдвига фазы

Мы также можем найти частоту среза на графике Найквиста, если вспомнить, что сдвиг фазы на 90°, создаваемый фильтром первого порядка, центрирован относительно частоты среза. Другими словами, фазовый сдвиг при ω составляет +45° или –45°. Вектор, нарисованный в комплексной плоскости, будет иметь угол +45° или –45°, если его действительная и мнимая части имеют одинаковые абсолютные значения, и это приводит нас к тем же геометрическим соотношениям, которые мы обнаружили при рассмотрении частоты среза с точки зрения амплитуды отклика.

Рисунок 6 – Частота среза фильтра нижних частот первого порядка на диаграмме НайквистаРисунок 7 – Частота среза фильтра верхних частот первого порядка на диаграмме Найквиста

Частота раздела

Тут самое время задуматься о частоте раздела. Обычно частота раздела выбирается на ровных горизонтальных участках, вдали от резонансов и завалов, стараясь обойти внезапные неравномерности как потенциальные источники искажений… А если вспомнить что существует фаза, о которой мало известно, а если известно, то векторно ачх на бумажке не сложишь, а из-за кривизны фаз даже на идеально ровной ачх что-то вылезет, что-то провалится в большей или меньшей степени. Также надо помнить что может дать сам динамик, особенно ВЧ, скажем не надо заставлять дюймовый купольник играть от двух, а тем более одного килогерца, даже если он способен их отыграть по АЧХ.

Итак, смотрим какие уникальные динамики нам достались. Высокочастотник начинает валить с 1,3 кгц, значит ниже его пускать нельзя. С другой стороны низкочастотник пытается играть по самые 10 кгц, с переменным успехом. Однако здравый смысл подсказывает, что выше килогерца его пускать плохая затея. И что спрашивается делать, если рабочие диапазоны динамиков не пересекаются?

Тут есть два варианта: если спады имеют адекватную крутизну, то лучше всего сводить в ямку, особенно если ямка получается широкой. В случае же нашем, когда спады круты как обрывы, надо держатся подальше от самого крутого из них. Чаще всего это может случится с высокочастотником, им всегда тяжко работать у нижней границы диапазона, поэтому им целесообразнее облегчить жизнь возлагая воспроизведение нижней части диапазона на НЧ динамик, который отыграет хоть плохо, но не нагадит. Поэтому ограничиваем диапазон участком от 1,5 кгц до 2,2 кгц.

Что такое электрический фильтр

Электрический фильтр – это устройство для выделения желательных компонентов спектра (частот) электрического сигнала и/или для подавления нежелательных. Для остальных частот, которые не входят в полосу пропускания, фильтр создает большое затухание, вплоть до полного их исчезновения. Характеристика идеального фильтра должна вырезать строго определенную полосу частота и “давить” другие частоты до полного их затухания. Ниже пример идеального фильтра, который пропускает частоты до какого-то определенного значения частоты среза.

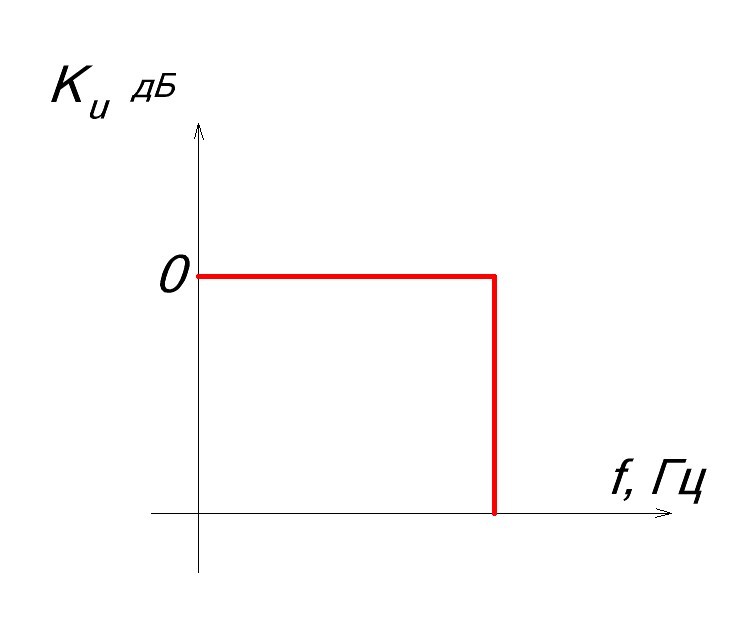
На практике такой фильтр реализовать нереально. При проектировании фильтров стараются как можно ближе приблизиться к идеальной характеристике. Чем ближе характеристика АЧХ к идеальному фильтру, тем лучше он будет исполнять свою функцию фильтрации сигналов.

Фильтры, которые собираются только на пассивных радиоэлементах, таких как катушка индуктивности, конденсатор, резистор, называют пассивными фильтрами. Фильтры, которые в своем составе имеют один или несколько активных радиоэлементов, типа транзистора или , называют активными фильтрами.

В нашей статье мы будем рассматривать пассивные фильтры и начнем с самых простых фильтров, состоящих из одного радиоэлемента.

RС-фильтры

RС-фильтр высоких частот

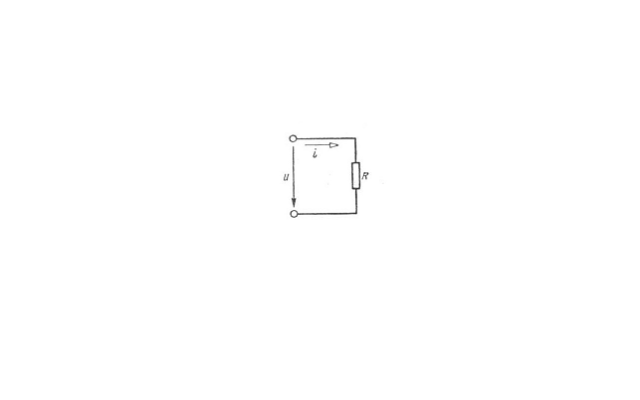
Схема RC-фильтра верхних (высоких) частот и его амплитудно-частотная характеристика показаны на рис. 1.

Рис. 1 — Схема и амплитудно-частотная характеристика высокочастотного CR-фильтра.

В этой схеме входное
напряжение прикладывается и к резистору,
и к конденсатору. Выходное же напряжение
снимается с сопротивления. При уменьшении
частоты сигнала возрастает реактивное
сопротивление конденсатора, а
следовательно, и полное сопротивление
цепи. Поскольку входное напряжение
остается постоянным, то ток, протекающий
через цепь уменьшается. Таким образом,
снижается и ток через активное
сопротивление, что приводит к уменьшению
падения напряжения на нем.

Фильтр характеризуется
затуханием, выраженным в децибелах,
которое он обеспечивает на заданной
частоте. RC-фильтры
рассчитываются таким образом, чтобы на выбранной частоте среза коэффициент передачи снижался приблизительно на 3
дБ (т.е. составлял 0,707 входного значения сигнала). Частота среза фильтра по уровню — 3 дБ определяется по формуле:

RС-фильтр низких частот

Фильтр низких частот имеет аналогичную структуру,
только емкость и сопротивление там
меняются местами. Амплитудно-частотную
характеристику такого фильтра можно
представить как зеркальное отображение
АЧХ предыдущего.

Рис. 2 — Схема и амплитудно-частотная характеристика низкочастотного RC-фильтра.

В этой цепи входное
напряжение также прикладывается и к
резистору, и к конденсатору, но выходное
напряжение снимается с конденсатора.
При увеличении частоты сигнала реактивное
сопротивление конденсатора, а
следовательно, и полное сопротивление
уменьшаются. Однако, поскольку это
полное сопротивление состоит из
реактивного и фиксированного активного
сопротивлений, его значение уменьшается
не так быстро, как реактивное сопротивление.
Следовательно, при увеличении частоты
снижение реактивного сопротивления (относительно полного сопротивления) приводит к уменьшению выходного напряжения. Частота среза этого фильтра по уровню -3 дБ также определяется по формуле предыдущего фильтра.

Рассмотренные
выше фильтры представляют собой RC-цепи,
которые характеризуются тремя параметрами,
а именно: активным, реактивным и полным
сопротивлениями. Обеспечиваемая этими
RC-фильтрами величина затухания зависит от отношения
активного или реактивного сопротивления
к полному сопротивлению.

При расчете любого RC-фильтра можно задать номинал либо резистора, либо конденсатора и вычислить значение другого элемента фильтра на заданной частоте среза. При практических расчетах
обычно задают номинал сопротивления,
поскольку он выбирается на основании
других требований. Например, сопротивление
фильтра является его выходным или
входным полным сопротивлением.

Полосовой RC-фильтр

Соединяя фильтры
верхних и нижних частот, можно создать
полосовой RC-фильтр,
схема и амплитудно-частотная характеристика
которого приведены на рис. 3.

Рис. 3 — Схема и АЧХ полосового RC-фильтра.

На схеме рис. 2. R₁ — полное входное сопротивление; R₂ —
полное выходное сопротивление, а частоты
низкочастотного и высокочастотного
срезов определяются по формулам:

Следует отметить,
что значение верхней частоты среза
()
должно быть по крайней мере быть в 10 раз
больше нижней частоты среза (),
поскольку только в этом случае
полосно-пропускающий фильтр будет
работать достаточно эффективно.

Многозвенные RC-фильтры

Одиночный RC-фильтр
не может обеспечить достаточного
подавления сигналов вне заданного
диапазона частот, поэтому для формирования
более крутой переходной области довольно
часто используют многозвенные фильтры
(рис. 4, 5). Частота среза многозвенного
фильтра определяется по формуле ВЧ, НЧ
RC-фильтра.
Добавление каждого звена приводит к
увеличению затухания на заданной частоте
среза примерно на 6 дБ.

Рис. 4 — Многозвенный высокочастотный фильтр

Рис. 5 — Многозвенный низкочастотный фильтр

Как собрать фильтр низких частот

Инструкция, как правильно сделать фильтр низких частот полезна для многих. В радиотехнике всегда требуется изготавливать фильтры разной высотности. И сделать самостоятельно фильтр низких частот не так уж сложно.

Вот, что нужно для изготовления фильтра низких частот:

• Разнообразные детали для припаиваня к печатной плате.
• Стеклотекстролит для печатной платы.
• Источник тока.
• Паяльник простой.

Далее распечатываем рисунок дорожек для платы и переносим его на нашу заготовку.

Если дорожки получаются не четкими, их следует дорисовать, используя лак. После того, как все перенесено, необходимо очистить плату при помощи специального раствора.

Создать раствор можно из лимонной кислоты и перекиси водорода. Их смешивают в пропорции 1:3 соответственно. Для более быстрого действия раствора туда добавляется катализатор — соль на кончике ножа.

Как только готов раствор, в него помещается плата и выжидается время до полной очистки. Медь, которая осталась на поверхности дорожек должна полностью раствориться. По окончании очистки платы необходимо ополоснуть ее под проточной водой.

По окончании процесса можно начать припаивать детали. Для того, чтобы сделать все точно, обратитесь к видео мастер-классу по припаиванию деталей.

Таким образом, вы заметили, насколько просто самостоятельно создать фильтр низких частот. По такому же принципу вы можете самостоятельно придумать схему изготовления и фильтра высокой частотности.

Цифровые фильтры

Большую часть информации и вывод формул я взял из книги Digital Signal Processing: A Practical Approach — очень рекомендую, она есть в русской версии — Цифровая обработка сигналов. Практический подход, заинтересованные найдут PDF в сети.

Хочу сделать важное замечание. Тема построения и рассчитывания фильтра действительно очень сложна, содержит массу тонкостей и нюансов, требует знания и понимания теории

В этой статье я покажу, как рассчитать формулы фильтра Баттервота, чтобы у читателя возникло понимание, откуда выводятся эти формулы. Но почему именно такие исходные формулы, почему именно такие замены — можно понять лишь погрузившись в глубокую теорию цифровой обработки сигналов.

Когда я начинал гуглить код фильтров, я сразу находил множество непонятного математического кода, и хотелось хоть чуть-чуть понять, откуда берутся такие рассчетные формулы. Осциллятор, огибающая, дилей — понимание и программирование работы этих составляющих лично мне кажется интуитивным, но только не фильтров. Этой статьей я хочу пробудить интерес к цифровой обработке сигналов) Буду рад, если возникнет желание разобраться в этой теме более основательно.

Вам нужно знать (хотя бы немножко) такие термины как свертка, импульсная характеристика фильтра, передаточная функция фильтра.

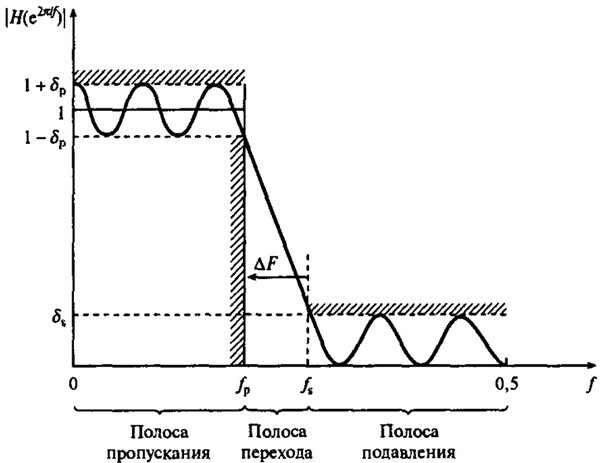
Аппроксимация АЧХ идеального фильтра (картинка из советского учебника, не нашел исходник)

Фильтр изменяет сигнал, «убирая» в нем выбранные частоты. Существующие фильтры не идеальны. Полоса пропускания — полоса частот, которую фильтр «не затрагивает» (на графике есть некоторая изменения — особенность неидеального представленного фильтра). Полоса подавления — полоса нежелательных частот. В полосе перехода происходит спад частот. Естественно, фильтр ближе к «идеальному» тем, насколько меньше он искажает полосу пропускания, насколько сильно он подавляет частоты в полосе подавления и насколько узка полоса перехода. Есть разные «приближения» фильтров — фильтр Чебышёва, Баттервота, и так далее — их вы найдете в книжках и на просторах сети.

Эквалайзер

Часто при обработке звука мы хотим изменить его характер/окраску/тембр. Сделать звук более басовым, убрать верхние частоты, или наоборот, сделать звук «прозрачным», оставив лишь середину и верха. Уверен, многие люди, не работавшие с обработкой звука, знают что такое эквалайзер — они есть акустических колонках, музыкальных центрах, магнитофонах, плеерах, и т.д. Эквалайзер — это набор фильтров, каждый из которых изменяет амплитуду сигнала в его выбранной полосе частот. На бытовых колонках это, обычно, 2-3 крутилки — низкие частоты, средние и верха, с фиксированными полосами частот.

В Winamp’овском эквалайзере уже есть 10 заранее определенных полос.

Скриншот эквалайзера в плеере Winamp

В мире обработки звука существует множество плагинов-эквалайзеров, на любой вкус и цвет. Плагин Fab Filter Pro Q (скриншот в начале статьи) — это графический эквалайзер, позволяющий создавать большое число полос и редактировать их параметры.

Каждая полоса в эквалайзере — это, по сути, фильтр частот. Фильтры частот изменяют тембральные/частотные характеристики сигнала. В электронике существуют много типов и классификаций фильтров, с соответствующими характеристиками и параметрами — смотрим википедию. Мы рассмотрим и запрограммируем самые простые фильтры: НЧ, ВЧ и полосовой фильтры.

Что такое электрический фильтр

Электрический фильтр – это устройство для выделения желательных компонентов спектра (частот) электрического сигнала и/или для подавления нежелательных. Для остальных частот, которые не входят в полосу пропускания, фильтр создает большое затухание, вплоть до полного их исчезновения. Характеристика идеального фильтра должна вырезать строго определенную полосу частота и “давить” другие частоты до полного их затухания. Ниже пример идеального фильтра, который пропускает частоты до какого-то определенного значения частоты среза.

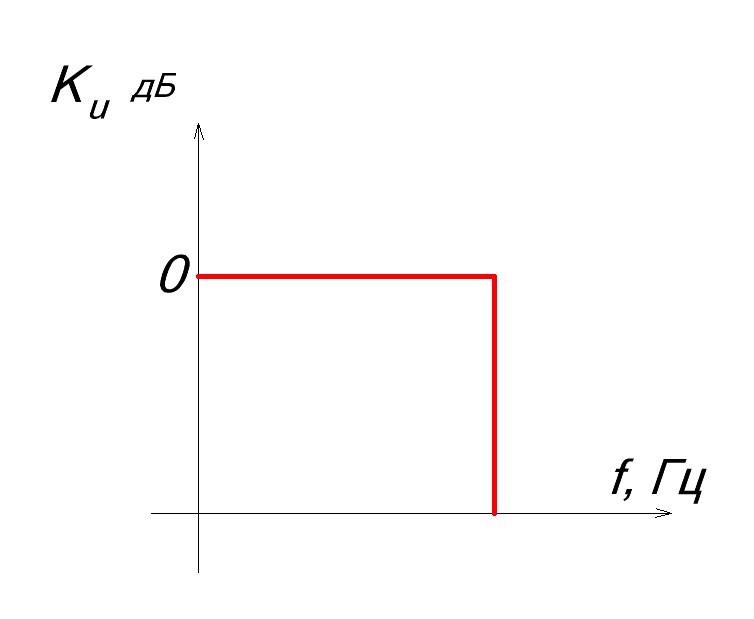
На практике такой фильтр реализовать нереально. При проектировании фильтров стараются как можно ближе приблизиться к идеальной характеристике. Чем ближе характеристика АЧХ к идеальному фильтру, тем лучше он будет исполнять свою функцию фильтрации сигналов.

Фильтры, которые собираются только на пассивных радиоэлементах, таких как катушка индуктивности, конденсатор, резистор, называют пассивными фильтрами. Фильтры, которые в своем составе имеют один или несколько активных радиоэлементов, типа транзистора или , называют активными фильтрами.

В нашей статье мы будем рассматривать пассивные фильтры и начнем с самых простых фильтров, состоящих из одного радиоэлемента.

Фазировка динамиков

На этом сведение подходит в концу. Остается только определиться с фазировкой динамиков. Тут есть как минимум три способа: на слух, по форме АЧХ и по фазовому сдвигу на частоте раздела. Если у динамиков АЧХ и ФЧХ в меру линейная, и фильтр фазу на разделе сильно не накручивает, то при смене правильной фазы на неправильную на частоте раздела появится глубокий провал, пропустить его сложно. В таком случае стоит подгонять фазу по по ее сдвигу. Сделать это можно осциллографом подавая на горизонтальную развертку сигнал с усилителя, а на вертикальное отклонение с микрофона.

Подают на вход усилителя синус с частотой раздела и не меняя взаимного расположения микрофона и колонки переключают ВЧ и НЧ динамики. По одинаковости фигур Лиссажу делается вывод о равенстве фаз излучателей. Этот метод хорошо подходит для фильтров первого порядка. С кривизной наших динамиков этот метод себя не оправдывает, поэтому сравниваем АЧХ при разной фазировке.

Второй вариант заметно хуже. Однако и первый не предел мечтаний, но так как двигать индуктивности катушек не просто, а ковыряться дальше уже лень, то все было оставлено как есть.

Электромагнитная совместимость частотных преобразователей

Электромагнитная совместимость технических средств — это нормальная (с требуемым качеством) работоспособность технического оборудования в реальной окружающей обстановке несмотря на непреднамеренное воздействие электромагнитных помех и способность не создавать недопустимых помех другой технике.

Все модели векторных преобразователей частоты оснащаются сетевыми фильтрами, чем обеспечивается необходимый уровень ЭМС. Фильтры допускается не применять в диапазоне до 30 кВт. Все преобразователи частоты большей мощности снабжаются встроенными фильтрами по умолчанию. Встроенный фильтр даёт возможность доводить до минимума наводки и помехи в электронной технике.

Влияние помех на приводное оборудование

В промышленности большая часть электропотребления приходится на вентиляторы, насосы, компрессоры, конвейеры и лебёдки, приводы технологических установок.  Механическая часть всего этого хозяйства приводится в действие асинхронными двигателями переменного тока. Режимное управление работы асинхронных двигателей, включая сокращение потребления ими электроэнергии, осуществляется с помощью специализированных устройств – преобразователей частоты. Польза их заключается в значительном облегчении пусковых режимов и работы непосредственно асинхронных двигателей. Однако иногда частотные преобразователи оказывают и нежелательное влияние на двигатель.

В виду особенной конструкции преобразователя частоты, его напряжение и ток на выходе имеют форму всплеска с огромным числом помех. Выпрямитель преобразовательного устройства, потребляя нелинейный ток, создаёт высшие гармоники, тем самым загрязняя электрическую сеть. Инвертор частотного преобразователя (ШИМ) – генерирует широкий спектр высокочастотных гармоник.

Электропитание обмоток двигателя таким нестандартным током подчас доводит до теплового и электрического пробоя изоляции обмоток двигателя, износу изоляции, увеличению степени акустических шумов работающего мотора, эрозии подшипников. Помимо этого, частотные преобразователи источают помехи в электрической сети, что оказывает отрицательное воздействие на остальное электрооборудование, питающееся от этой же электросети. Для уменьшения неблагоприятного влияния гармонических искажений, создаваемых преобразователем частоты в процессе работы, на электросеть, для двигателя и самого преобразователя частоты используется фильтрация.

Практическая работа

Плавно переходим от теории к практике. Достались мне винтажные колонки под названием Kompaktbox B 9251. И первое что было сделано – произведено прослушивание.

С холодным камнем звук был в среднем не плох, а если говорить конкретно, то местами хороший, а местами как попало. С теплой лампой играть вообще отказались. На основе этих наблюдений был сделан вывод о наличии глубоко зарытого потенциала. Вскрытие показало, что немецкие инженеры решили обойтись одним единственным конденсатором последовательно с ВЧ головкой. Измерение АЧХ дало страшную картину

На рисунке АЧХ одной колонки, кривая с глубокой дыркой на 6 кгц из-за плохого контакта разъема, на нее внимание не обращать. АЧХ отдельно ВЧ и НЧ приведены ниже

П-образные

Можно сказать, что эти фильтры такие же, как и Г-образные, но к ним присоединяется вдобавок еще одна часть вначале. Все, что будет написано для Т-образных, будет верно и для П-образных. Отличия лишь заключаются в том, что у них увеличится шунтирующее действие на радиоцепь, стоящую спереди.

Для того чтобы рассчитать П-образный фильтр, вам надо будет использовать формулу делителя напряжения и добавить дополнительное шунтирующее сопротивление первого элемента.

Вот вам примеры перехода Г-образного RC фильтра в П-образный RC также высоких частот:

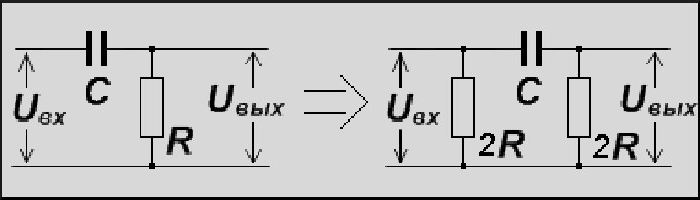
На изображении можно заметить, что к исходной цепи добавляется еще один резистор 2R, расположенный параллельно первому.

Вот пример преобразования в RL:

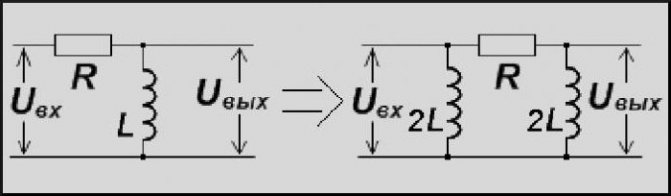
Здесь вместо резисторра выстпает катушка индуктивности. Так же добавляется вторая (2L), расположенная параллельно первой.

И третий пример — преобразования в LC:

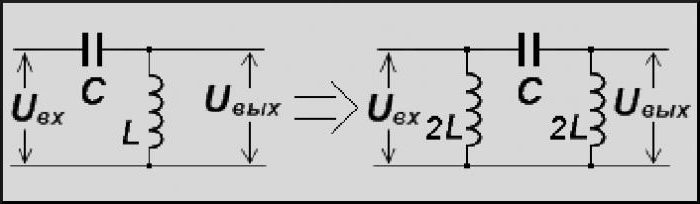
How inductance and capacitance work

Three types of load resistance are distinguished in electrical engineering: ohmic, inductive and capacitive resistance. Ohmic resistance is independent of the frequency and always remains the same. In contrast, inductive and capacitive resistances change with the frequency of the applied voltage. This is due to the inductive reactance \(X_L\) and the capacitive reactance \(X_C\).

If an alternating current flows through a coil, then a magnetic field is built up and taken down in it. The electronic engineer speaks of induction. The induced voltage counteracts the applied voltage, resulting in the inductive reactance \(X_L\). The effect of induction increases with increasing frequency. The current flow in the coil is always delayed, so the voltage always rushes afterwards.

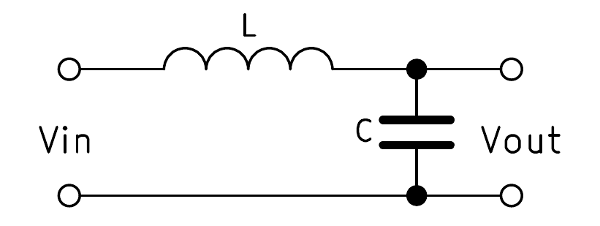
The capacitor is, in principle, a battery with a very small capacity. It can be charged and discharged again. The capacitor acts like a nearly infinite resistance in a DC circuit. In an AC circuit, however, it is permanently charged and discharged by the alternating current direction. Basically, the current does not really flow through the capacitor. During this continuous charging and discharging, the capacitive reactance \(X_C\) is created. The higher the frequency, the shorter the charging cycles of the capacitor and the lower its reactance.

Полосовые резонансные фильтры

Полосовые резонансные частотные фильтры – предназначены для выделения, или режекции (вырезания) определённой полосы частот. Резонансные частотные фильтры могут состоять из одного, двух, или трех колебательных контуров, настроенных на определённую частоту. Резонансные фильтры обладают наиболее крутым подъёмом (или спадом) АЧХ, по сравнению с другими (не резонансными) фильтрами. Полосовые резонансные частотные фильтры могут быть одноэлементными — с одним контуром, Г-образными – с двумя контурами, Т и П-образными – с тремя контурами, многозвенными – с четырьмя и более контурами.

На рисунке представлена схема Т-образного полосового резонансного фильтра, предназначенного для выделения определённой частоты. Состоит он из трёх колебательных контуров. CL и CL – последовательные колебательные контуры, на резонансной частоте имеют малое сопротивление протекающему току, а на других частотах наоборот – большое. Параллельный контур CL наоборот, имеет большое сопротивление на резонансной частоте, обладая малым сопротивлением на других частотах. Для расширения ширины полосы пропускания такого фильтра, уменьшают добротность контуров, изменяя конструкцию катушек индуктивности, расстраивая контура «вправо, влево» на частоту, немного отличающуюся от центральной резонансной, параллельно контуру CL подключают резистор.

На следующем рисунке представлена схема Т-образного режекторного резонансного фильтра, предназначенного для подавления определённой частоты. Он, как и предыдущий фильтр состоит из трёх колебательных контуров, но принцип выделения частот у такого фильтра другой. CL и CL – параллельные колебательные контуры, на резонансной частоте имеют большое сопротивление протекающему току, а на других частотах – маленькое. Параллельный контур CL наоборот, имеет малое сопротивление на резонансной частоте, обладая большим сопротивлением на других частотах. Таким образом, если предыдущий фильтр резонансную частоту выделяет, а остальные частоты подавляет, то этот фильтр, беспрепятственно пропускает все частоты, кроме резонансной частоты.

Порядок расчёта полосовых резонансных фильтров основан всё на том же делителе напряжения, где в качестве единичного элемента выступает LC контур с его характеристическим сопротивлением. Как рассчитывается колебательный контур, определяются его резонансная частота, добротность и характеристическое (волновое) сопротивление вы можете найти в статье Колебательный контур.

PSU Designer

Очень полезная программа. С ее помощью легко рассчитываются любые источники питания — мостовые, одно- и двухполупериодные, на кенотронах и диодах, с L и C-фильтром. В базе данных уже содержатся необходимые данные наиболее популярных выпрямителей, вам остается лишь задать напряжение на вторичной обмотке сетевого трансформатора и ток (сопротивление) нагрузки. Программа симулирует форму напряжения и тока в любой точке схемы и предупреждает, если какое-нибудь предельно допустимое значение для выпрямителя превышено. Новая версия PSU Designer позволяет сохранять файлы и редактировать их (информация с сайта «Салон AV»)

Временная область и частотная область

Когда вы смотрите на электрический сигнал на осциллографе, вы видите линию, которая представляет изменения напряжения относительно времени. В любой конкретный момент времени сигнал имеет только одно значение напряжения. На осциллографе вы видите представление сигнала во временной области.

Типовая осциллограмма проста и интуитивно понятна, но она также имеет некоторые ограничения, поскольку она напрямую не раскрывает частотный состав сигнала. В отличие от представления во временной области, в котором один момент времени соответствует только одному значению напряжения, представление в частотной области (также называемое спектром) передает информацию о сигнале посредством определения различных частотных компонентов, которые представлены одновременно.

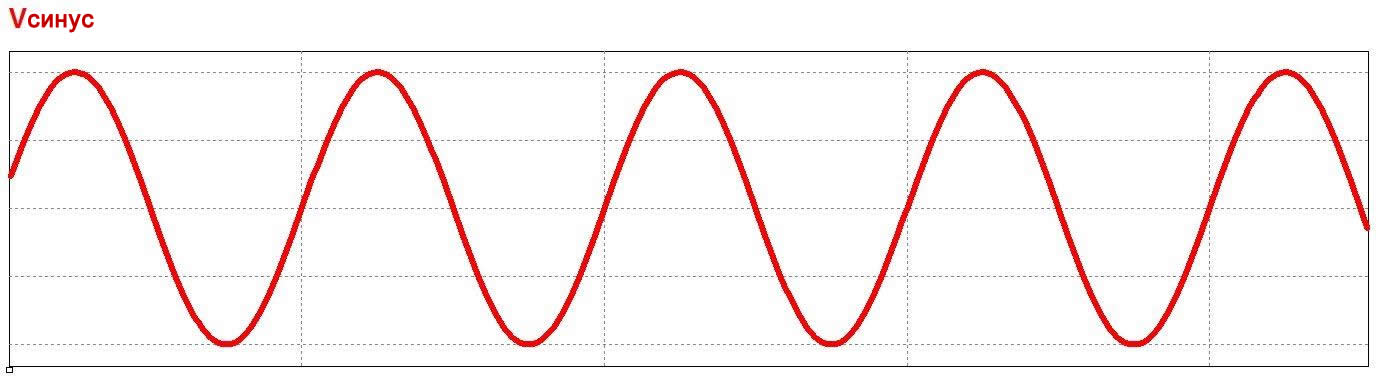
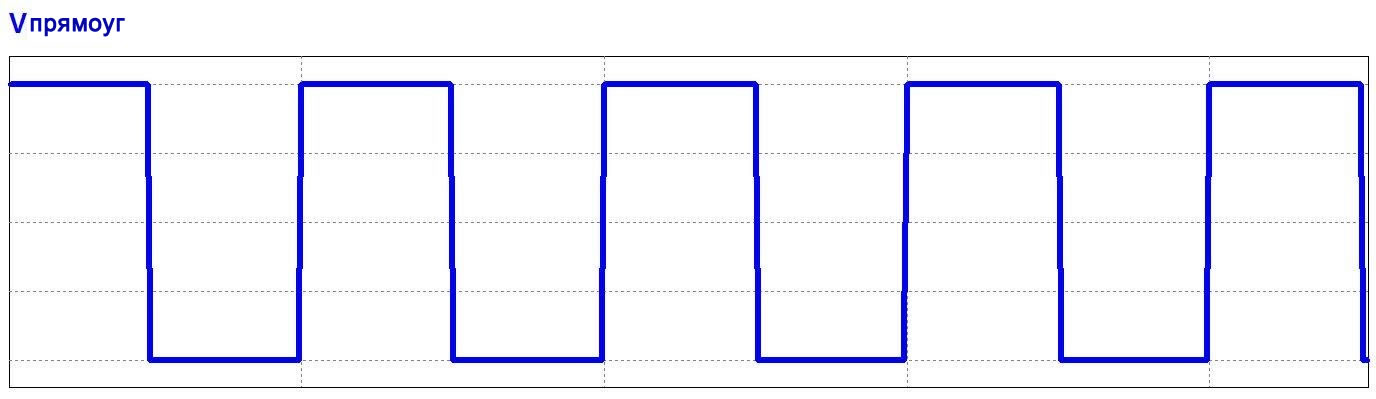Рисунок 1 – Представления во временной области синусоидального (вверху) и прямоугольного (внизу) сигналов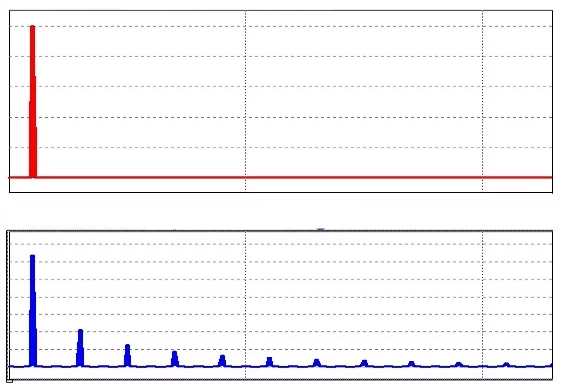Рисунок 2 – Частотные представления синусоидального (вверху) и прямоугольного (внизу) сигналов

Похожие записи:

Характеристики диодов 1n4007, д242, д226, кд202в Активное и индуктивное сопротивление Как определить катод и анод у светодиода Топ-7 лучших терморегуляторов: какой выбрать, для теплого пола, с датчиком, отзывы, цена Автоматическое включение фар при запуске двигателя автомобиля своими руками Топ новых гаджетов 2020 года