Расчет lc фильтра

Порядок фильтра и его добротность

Следующий параметр, с которым надо определиться — это порядок фильтра и его добротность. В данной статье будут рассматриваться два порядка, первый и второй.

С первым все просто: есть катушка, есть конденсатор, считаем их параметры под требуемую частоту среза и при надобности корректируем значения до получения желаемой АЧХ, ФЧХ, ИЧХ.
Со вторым порядком по-хитрее, там уже две катушки и два конденсатора. От значений номиналов зависит такой параметр как добротность, он определяет крутизну спада АЧХ и в некоторой степени сдвиг фазы. Поскольку влияние фазового сдвига и крутизны умозрительно не прикинешь, остается просто выбрать в какую сторону думать. А думать тут в сторону низкой добротности, читай больше индуктивности в катушках, меньше емкости в конденсаторах.

Как выбрать порядок. Тут руководствуются уже знакомыми соображениями о том, на что способны излучатели, в особенности высокочастотник. Если большой ход ему противопоказан (как в нашем случае) то предпочтение отдаем второму порядку.

Для полноты картины следует упомянуть, что порядок также определяет степень совместной работы динамиков, но это уже информация для самостоятельного размышления.

Подпишись на RSS!

Подпишись на RSS и получай обновления блога!

Получать обновления по электронной почте:

- Пленочные конденсаторы — применение в энергетике
  9 апреля 2021
- Поворотное устройство для солнечного коллектора
  15 марта 2021
- Выбор подпрограммы с помощью кнопки
  11 марта 2021
- Керамические конденсаторы SMD, параметры
  4 марта 2021
- Программа для проверки выходных буферов PIC16F676 и PIC16F628A
  21 февраля 2021

- Зарядное устройство для автомобильных аккумуляторов — 242 124 просмотров
- Стабилизатор тока на LM317 — 176 995 просмотров
- Стабилизатор напряжения на КР142ЕН12А — 128 049 просмотров
- Реверсирование электродвигателей — 104 705 просмотров
- Зарядное для аккумуляторов шуруповерта — 101 144 просмотров
- Карта сайта — 101 064 просмотров
- Зарядное для шуруповерта — 89 943 просмотров
- Самодельный сварочный аппарат — 89 701 просмотров
- Схема транзистора КТ827 — 85 771 просмотров
- Регулируемый стабилизатор тока — 85 505 просмотров

- DC-DC (5)
- Автомат откачки воды из дренажного колодца (5)
- Автоматика (35)
- Автомобиль (3)
- Антенны (2)
- Ассемблер для PIC16 (3)
- Блоки питания (30)
- Бурение скважин (6)
- Быт (11)
- Генераторы (1)
- Генераторы сигналов (8)
- Датчики (4)
- Двигатели (7)
- Для сада-огорода (11)
- Зарядные (17)
- Защита радиоаппаратуры (8)
- Зимний водопровод для бани (2)
- Измерения (41)
- Импульсные блоки питания (2)
- Индикаторы (6)
- Индикация (10)
- Как говаривал мой дед … (1)
- Коммутаторы (6)
- Логические схемы (1)
- Обратная связь (1)
- Освещение (3)
- Программирование для начинающих (19)
- Программы (1)
- Работы посетителей (7)
- Радиопередатчики (2)
- Радиостанции (1)
- Регуляторы (5)
- Ремонт (1)
- Самоделки (12)
- Самодельная мобильная пилорама (3)
- Самодельный водопровод (7)
- Самостоятельные расчеты (37)
- Сварка (1)
- Сигнализаторы (5)
- Справочник (13)
- Стабилизаторы (16)
- Строительство (2)
- Таймеры (4)
- Термометры, термостаты (27)
- Технологии (21)
- УНЧ (2)
- Формирователи сигналов (1)
- Электричество (4)
- Это пригодится (14)
Архивы
Выберите месяц Апрель 2021 (1) Март 2021 (3) Февраль 2021 (2) Январь 2021 (1) Декабрь 2020 (1) Ноябрь 2020 (1) Октябрь 2020 (1) Сентябрь 2020 (2) Июль 2020 (2) Июнь 2020 (1) Апрель 2020 (1) Март 2020 (3) Февраль 2020 (2) Декабрь 2019 (2) Октябрь 2019 (3) Сентябрь 2019 (3) Август 2019 (4) Июнь 2019 (4) Февраль 2019 (2) Январь 2019 (2) Декабрь 2018 (2) Ноябрь 2018 (2) Октябрь 2018 (3) Сентябрь 2018 (2) Август 2018 (3) Июль 2018 (2) Апрель 2018 (2) Март 2018 (1) Февраль 2018 (2) Январь 2018 (1) Декабрь 2017 (2) Ноябрь 2017 (2) Октябрь 2017 (2) Сентябрь 2017 (4) Август 2017 (5) Июль 2017 (1) Июнь 2017 (3) Май 2017 (1) Апрель 2017 (6) Февраль 2017 (2) Январь 2017 (2) Декабрь 2016 (3) Октябрь 2016 (1) Сентябрь 2016 (3) Август 2016 (1) Июль 2016 (9) Июнь 2016 (3) Апрель 2016 (5) Март 2016 (1) Февраль 2016 (3) Январь 2016 (3) Декабрь 2015 (3) Ноябрь 2015 (4) Октябрь 2015 (6) Сентябрь 2015 (5) Август 2015 (1) Июль 2015 (1) Июнь 2015 (3) Май 2015 (3) Апрель 2015 (3) Март 2015 (2) Январь 2015 (4) Декабрь 2014 (9) Ноябрь 2014 (4) Октябрь 2014 (4) Сентябрь 2014 (7) Август 2014 (3) Июль 2014 (2) Июнь 2014 (6) Май 2014 (4) Апрель 2014 (2) Март 2014 (2) Февраль 2014 (5) Январь 2014 (4) Декабрь 2013 (7) Ноябрь 2013 (6) Октябрь 2013 (7) Сентябрь 2013 (8) Август 2013 (2) Июль 2013 (1) Июнь 2013 (2) Май 2013 (4) Апрель 2013 (7) Март 2013 (7) Февраль 2013 (7) Январь 2013 (11) Декабрь 2012 (7) Ноябрь 2012 (5) Октябрь 2012 (2) Сентябрь 2012 (10) Август 2012 (14) Июль 2012 (5) Июнь 2012 (21) Май 2012 (13) Апрель 2012 (4) Февраль 2012 (6) Январь 2012 (6) Декабрь 2011 (2) Ноябрь 2011 (9) Октябрь 2011 (14) Сентябрь 2011 (22) Август 2011 (1) Июль 2011 (5)

Как рассчитать короб

Акустические системы, в том числе и сабвуферы, рассчитывают с помощью компьютерных программ. Наиболее часто используют «WinISD» и «JBL Speakershop».

Исходные данные для расчётов — технические характеристики динамиков из встроенных в программы баз данных, или введённые вручную. Как минимум необходимо задать основные, о которых упоминалось выше.

Софт также позволяет вести расчёты в «противоположном направлении», подобрать динамик, который обеспечит наилучшую отдачу при заданных параметрах корпуса.

Наиболее простые акустические формы, такие как закрытый ящик и фазоинвертор, не требуют высокой точности. Их можно рассчитать вручную с помощью формул.

Расчёт закрытого ящика

Цель расчёта — основываясь на исходных данных (трёх основных параметрах динамика) подобрать внутренний объём колонки.Если отношение паспортного значения резонансной частоты (F_s) к добротности (Q_ts) меньше 100, такой динамик лучше не устанавливать в закрытый ящик.

Запертый в корпусе закрытого ящика воздух, сжимаясь под действием диффузора, увеличивает жёсткость подвеса. В результате резонансная частота и добротность акустической системы возрастает.

Формулы, связывающие резонансную частоту (F_c), добротность (Q_tc) и объём (V_b) колонки с аналогичными паспортными параметрами (F_s, Q_ts и V_as) динамика приведена на рисунке.

Формулы, связывающие резонансную частоту (Fc), добротность (Qtc) и объём (Vb) колонки с аналогичными паспортными параметрами (Fs, Qts и Vas) динамика

Как следует из формул, если объём корпуса равен эквивалентному, значения параметров возрастают в 1,4 раза, и вдвое, когда объём закрытого ящика втрое меньше V_as.

Подбирая с помощью формул допустимый объем корпуса, стремятся, чтобы резонансная частота колонки (F_c) не превышала 50 Гц, а добротность (Q_tc) была близка к 0,7.

Расчёт фазоинвертора

Для этого акустического оформления выбирают динамики с добротностью 0,3—0,5 и отношением резонансной частоты к добротности не мене 50. Кроме объёма сабвуфера, вычисляют параметры (площадь сечения, диаметр и длину трубы) порта фазоинвертора.

Параметры короба подбирают по тем же формулам, что и в случае с закрытым ящиком, но при этом ориентируются на добротность колонки (Q_tc) в пределах 0,6—0,65.

Параметры порта рассчитывают, опираясь на значение частоты настройки фазоинвертора (F_b) выбранной равной резонансной частоте динамика (F_s) или немного меньше. Формулы для расчёта площади сечения, диаметра и длины порта фазоинвертора показаны на рисунке.

Формулы для расчёта площади сечения, диаметра и длины порта фазоинвертора

В приведённых формулах:

s_min — минимальная площадь (м2) сечения порта фазоинвертора;
D — диаметр (м) динамика;
X_max — максимальный ход (м) диффузора от нулевого положения, указывается в технических характеристиках динамика;
F_b — резонансная частота (Гц) фазоинвертора;
d_min — минимальный диаметр (м) круглой трубы, используемой в качестве фазоинвертора;
L — длина (м) фазоинвертора;
L_max — максимальная длина (м) фазоинвертора.

Расчётная длина фазоинвертора может получиться больше рекомендованного максимального значения. Уменьшить практическую длину можно несколькими способами.

Размещение выхода круглого фазоинвертора заподлицо с плоскостью панели колонки даёт выигрыш в длине до 0,85 диаметра фазоинвертора. Фланцы на конце трубы ещё больше усиливают эффект.

Около 15% длины можно сэкономить, разместив фазоинвертор вплотную к одной из сторон колонки.

Использование порта в виде усечённого конуса круглого или прямоугольного сечения поможет уменьшить длину фазоинвертора до 35%. Конфигурация в виде песочных часов — до 40%.

Расчет амплитудно-частотной характеристики фильтра

Мы можем рассчитать теоретическое поведение фильтра нижних частот, используя частотно-зависимую версию типового расчета делителя напряжения. Выходное напряжение резистивного делителя напряжения выражается следующим образом:

Рисунок 9 – Резистивный делитель напряжения

RC фильтр использует эквивалентную структуру, но вместо R₂ у нас конденсатор. Сначала мы заменим R₂ (в числителе) на реактивное сопротивление конденсатора (X_C). Далее нам нужно рассчитать величину полного сопротивления и поместить его в знаменатель. Таким образом, мы имеем

Реактивное сопротивление конденсатора указывает величину противодействия протеканию тока, но, в отличие от активного сопротивления, величина противодействия зависит от частоты сигнала, проходящего через конденсатор. Таким образом, мы должны рассчитать реактивное сопротивление на определенной частоте, и формула, которую мы используем для этого, следующая:

В приведенном выше примере схемы R ≈ 160 Ом, и C = 10 нФ. Предположим, что амплитуда V_вх равна 1 В, поэтому мы можем просто удалить V_вх из расчетов. Сначала давайте рассчитаем амплитуду V_вых на частоте необходимой нам синусоиды:

Амплитуда необходимого нам синусоидального сигнала практически не изменяется. Это хорошо, поскольку мы намеревались сохранить синусоидальный сигнал при подавлении шума. Этот результат неудивителен, поскольку мы выбрали частоту среза (100 кГц), которая намного выше частоты синусоидального сигнала (5 кГц).

Теперь посмотрим, насколько успешно фильтр ослабит шумовую составляющую.

Амплитуда шума составляет всего около 20% от первоначального значения.

Архивы

АрхивыВыберите месяц Апрель 2021 (1) Март 2021 (3) Февраль 2021 (2) Январь 2021 (1) Декабрь 2020 (1) Ноябрь 2020 (1) Октябрь 2020 (1) Сентябрь 2020 (2) Июль 2020 (2) Июнь 2020 (1) Апрель 2020 (1) Март 2020 (3) Февраль 2020 (2) Декабрь 2019 (2) Октябрь 2019 (3) Сентябрь 2019 (3) Август 2019 (4) Июнь 2019 (4) Февраль 2019 (2) Январь 2019 (2) Декабрь 2018 (2) Ноябрь 2018 (2) Октябрь 2018 (3) Сентябрь 2018 (2) Август 2018 (3) Июль 2018 (2) Апрель 2018 (2) Март 2018 (1) Февраль 2018 (2) Январь 2018 (1) Декабрь 2017 (2) Ноябрь 2017 (2) Октябрь 2017 (2) Сентябрь 2017 (4) Август 2017 (5) Июль 2017 (1) Июнь 2017 (3) Май 2017 (1) Апрель 2017 (6) Февраль 2017 (2) Январь 2017 (2) Декабрь 2016 (3) Октябрь 2016 (1) Сентябрь 2016 (3) Август 2016 (1) Июль 2016 (9) Июнь 2016 (3) Апрель 2016 (5) Март 2016 (1) Февраль 2016 (3) Январь 2016 (3) Декабрь 2015 (3) Ноябрь 2015 (4) Октябрь 2015 (6) Сентябрь 2015 (5) Август 2015 (1) Июль 2015 (1) Июнь 2015 (3) Май 2015 (3) Апрель 2015 (3) Март 2015 (2) Январь 2015 (4) Декабрь 2014 (9) Ноябрь 2014 (4) Октябрь 2014 (4) Сентябрь 2014 (7) Август 2014 (3) Июль 2014 (2) Июнь 2014 (6) Май 2014 (4) Апрель 2014 (2) Март 2014 (2) Февраль 2014 (5) Январь 2014 (4) Декабрь 2013 (7) Ноябрь 2013 (6) Октябрь 2013 (7) Сентябрь 2013 (8) Август 2013 (2) Июль 2013 (1) Июнь 2013 (2) Май 2013 (4) Апрель 2013 (7) Март 2013 (7) Февраль 2013 (7) Январь 2013 (11) Декабрь 2012 (7) Ноябрь 2012 (5) Октябрь 2012 (2) Сентябрь 2012 (10) Август 2012 (14) Июль 2012 (5) Июнь 2012 (21) Май 2012 (13) Апрель 2012 (4) Февраль 2012 (6) Январь 2012 (6) Декабрь 2011 (2) Ноябрь 2011 (9) Октябрь 2011 (14) Сентябрь 2011 (22) Август 2011 (1) Июль 2011 (5)

Определение частоты среза

Кривая на диаграмме Найквиста, конечно, не имеет типового спада характеристики, который мы хорошо знаем из графиков амплитудно-частотных характеристик, и фактически график Найквиста не дает нам конкретной информации о частоте среза схемы фильтра. Однако изучение взаимосвязи между частотой среза и кривой Найквиста является хорошим способом укрепить понимание концепции частоты среза в целом, а также даст нам некоторое представление об ограничениях подхода Найквиста для визуального изображения частотной характеристики.

Во-первых, нам нужно подумать о том, что на самом деле происходит на частоте среза, с точки зрения как амплитудно-частотной, так и фазо-частотной характеристики.

Частота среза относительно амплитуды

Вы, вероятно, знаете, что другое название для частоты среза – это «частота 3 дБ» (или –3 дБ), и это напоминает нам о том, что фильтр нижних частот первого порядка обеспечивает ослабление на 3 дБ (или, что эквивалентно, усилению –3 дБ), когда входная частота равна ω. Мы не используем децибелы на графике Найквиста, поэтому вместо –3 дБ мы используем соответствующий коэффициент передачи в разах, который равен \(\frac{1}{\sqrt{2}}\)

Когда мы работаем с графиком в полярной системе координат, мы всегда должны помнить о треугольниках; например, амплитуда (модуль) комплексного числа определяется как гипотенуза прямоугольного треугольника, два катета которого являются действительной и мнимой частями; а для вычисления фазы (угла) комплексного числа мы используем тригонометрические функции. Теперь, когда вы думаете с точки зрения треугольников, коэффициент \(\frac{1}{\sqrt{2}}\) дает вам какие-нибудь идеи?

Рисунок 2 – Прямоугольный треугольник. Длина катетов равна 1

Как показано выше, коэффициент \(\sqrt{2}\) вступает в игру всякий раз, когда у прямоугольного треугольника два катета равной длины. Если уменьшить длину катетов до 0,5, длина гипотенузы будет равна \(\sqrt{2} \times 0,5\), что то же самое, что \(\frac{1}{\sqrt{2}}\).

Рисунок 3 – Прямоугольный треугольник. Длина катетов равна 0,5

Итак, что же всё это значит? Рассмотрим следующий график Найквиста:

Рисунок 4 – Это график Найквиста для фильтра нижних частот первого порядка

Обратите внимание, что я не добавил часть графика, которая соответствует отрицательным частотам

Как видите, в самой нижней точке кривой коэффициент усиления фильтра равен \(\frac{1}{\sqrt{2}}\), где абсолютное значение действительной части равно абсолютному значению мнимой части; это и есть местоположение частоты среза на графике Найквиста для фильтра нижних частот первого порядка. То же самое отношение применяется к фильтру верхних частот первого порядка, за исключением того, что в этом случае частота среза находится в самой высокой точке кривой:

Рисунок 5 – Частота среза фильтра верхних частот первого порядка на диаграмме Найквиста

Разница заключается в том, что сдвиг фазы фильтра верхних частот с увеличением частоты изменяется от +90° до 0°, тогда как фаза фильтра нижних частот изменяется от 0° до –90°. Поскольку угол измеряется против часовой стрелки от положительной действительной оси, положительный сдвиг фазы отображается над действительной осью, а отрицательный сдвиг фазы отображается ниже действительной оси.

Также обратите внимание, что на этих двух графиках есть стрелки, указывающие в противоположных направлениях: на графике фильтра нижних частот стрелка указывает на начало координат, поскольку с увеличением частоты коэффициент усиления уменьшается; на графике фильтра верхних частот она указывает в сторону от начала координат, поскольку с увеличением частоты коэффициент усиления увеличивается

Частота среза относительно сдвига фазы

Мы также можем найти частоту среза на графике Найквиста, если вспомнить, что сдвиг фазы на 90°, создаваемый фильтром первого порядка, центрирован относительно частоты среза. Другими словами, фазовый сдвиг при ω составляет +45° или –45°. Вектор, нарисованный в комплексной плоскости, будет иметь угол +45° или –45°, если его действительная и мнимая части имеют одинаковые абсолютные значения, и это приводит нас к тем же геометрическим соотношениям, которые мы обнаружили при рассмотрении частоты среза с точки зрения амплитуды отклика.

Рисунок 6 – Частота среза фильтра нижних частот первого порядка на диаграмме НайквистаРисунок 7 – Частота среза фильтра верхних частот первого порядка на диаграмме Найквиста

Рис. 90. Схема бескаркасной намотки катушки

Если есть возможность, то для полимеризации клея катушку запекают в термостате при температуре 140 — 160° С в течение 1 ч.

Если такой возможности нет, то катушка должна быть высушена при комнатной температуре в течение суток. Иногда провод, в качестве которого предпочитают марку ПЭЛ, бывает покрыт каким-либо маслом.

Тогда перед намоткой или в ее процессе провод нужно протереть ваткой, смоченной смесью из 50% спирта и 50% бензина или, в крайнем случае, чистым бензином. Собранный и смонтированный фильтр, т. е. его конденсаторы и катушки, размещают на полочке, укрепленной внутри корпуса АС. Разумеется, все электрические соединения должны быть хорошо пропаяны во избежание шорохов и тресков, могущих возникнуть из-за плохих контактов.

Фильтры Чебышева

Квадрат модуля передаточной функции фильтра Чебышева определяется выражением

. (7.3)

Здесь — полином Чебышева. Модуль передаточной функции фильтра Чебышева равен единице на тех частотах, где обращается в нуль. График амплитудно-частотной характеристики фильтра Чебышева пятого порядка показан на рис. 7.3.

Рис. 7.3

Перечислим свойства частотных характеристик фильтров Чебышева.

В полосе пропускания АЧХ имеет равноволновой характер. На интервале имеется n точек, в которых функция достигает максимального значения, равного 1, или минимального значения, равного . Если n нечетно, , если n четно, .
Значение АЧХ фильтра Чебышева на частоте среза равно

При функция монотонно убывает и стремится к нулю.
Параметр определяет неравномерность АЧХ фильтра Чебышева в полосе пропускания:

Сравнение АЧХ фильтров Баттерворта и Чебышева показывает, что фильтр Чебышева обеспечивает большее ослабление в полосе пропускания, чем фильтр Баттерворта такого же порядка. Недостаток фильтров Чебышева заключается в том, что их фазочастотные характеристики в полосе пропускания значительно отличаются от линейных.
Для фильтров Баттерворта и Чебышева имеются подробные таблицы, в которых приведены координаты полюсов и коэффициенты передаточных функций различных порядков.

Важные характеристики АС

Для начала разберёмся чем характеризуется акустическая система. Тут три характеристики: амплитудная, фазовая и импедансная.

АЧХ считается наиболее важной, так как больше определяет звучание, впрочем не в ней счастье, ровная АЧХ еще не гарантия хорошего звука.

ФЧХ сама о себе не слышна, может быть слышен резкий перегиб фазы в точке раздела.

ИЧХ вовсе на звучание не влияет, зато влияет на усилитель, но не на каждый, а лишь на тот у которого высокое внутреннее сопротивление, в частности ламповые.

Из-за кривого импеданса многие колонки могут не спеться с лампой, вся неровность импеданса вылезет в АЧХ. В каком-то случае это может пойти на пользу, но надеяться на это не стоит, хотя бы потому, что такая акустика будет крайне чувствительна к усилителю, станут слышны лампы, их режимы, а сравнение с каменным усилителем становится вообще не корректным.

Потому, если задаться цель построить акустику мало чувствительную к усилителю, необходимо обеспечить постоянство импеданса во всем диапазоне частот, а это накладывает определенные ограничения. В частности это обязывает применять фильтра настроеные на равную частоту среза и имеющие равную добротность.

Это правило позволяет для настройки фильтра контролировать только линейность импеданса, что исключает необходимость измерения АЧХ фильтров и в случаи отсутствия хорошего микрофона в измерении ачх динамиков, то есть можно обойтись минимальным набором приборов: генератором (возможно программным) и вольтметром.

Что такое полосовой фильтр

Как следует из названия, полосовой фильтр фильтрует все частоты, пропуская только частоты, находящиеся в определенном диапазоне. Все частоты за пределами данного частотного диапазона ослабляются.

Есть два основных параметра определяющие характеристики полосового фильтра: полоса пропускания, где фильтр пропускает сигналы и полоса затухания, в которой сигналы ослабляются.

Идеальный полосовой фильтр имеет ровную полосу пропускания (усиление и отсутствие затухания сигнала по всей полосе пропускания) и полное затухание вне полосы пропускания. Кроме того, переход из полосы пропускания абсолютно резкий.

Но на практике невозможно создать идеальный полосовой фильтр. Реальный фильтр неспособен полностью задержать все частоты за границами желаемого диапазона частот. В частности, имеется область в непосредственной близости у границы заданного диапазона, где сигнал частично ослабляется, но не отфильтровывается полностью. Эта область носит название крутизна спада фильтра, и измеряется в дБ затухания на октаву. Как правило, при проектировании, стремятся сделать данный спад как можно более узким, что позволяет получить фильтр максимально приближенным к заданным параметрам.

Важные характеристики АС

АЧХ считается наиболее важной, так как больше определяет звучание, впрочем не в ней счастье, ровная АЧХ еще не гарантия хорошего звука. ФЧХ сама о себе не слышна, может быть слышен резкий перегиб фазы в точке раздела

Расчет полосового фильтра

Расчет полосового фильтра может стать очень сложным занятием даже при использовании операционных усилителей. Тем не менее можно немного упростить методику расчета, и в то же время сохранить производительность полосового фильтра на ОУ на приемлемом уровне.

Данная схема и методика расчета представляют собой хороший баланс между производительностью и простотой конструкцией фильтра.

Из рисунка видно, что помимо операционного усилителя схема еще содержит два конденсатора и три резистора.

Цифровой мультиметр AN8009
Большой ЖК-дисплей с подсветкой, 9999 отсчетов, измерение TrueRMS…

Подробнее

Пример упрощенного расчета элементов полосового фильтра на ОУ

Входные данные:

Резонансная частота f = 20Гц.
Добротность Q = 10.
Коэффициент передачи Hо = 5

Так как fmax – fmin = f / Q = 2Гц,

то полоса пропускания составит fmax = 21 Гц, fmin=19 Гц.

Будем исходить из того, что C1=C2=C=1мкФ

Тогда сопротивления резисторов можно рассчитать по следующим формулам:

В нашем случае получим следующие результаты:

R1 = 10 / (5*2*3,14*20*0,000001) = 15,9 кОм

R2 = 10 / ((2*10*10-5)*2*3,14*20*0,000001) = 408 Ом

R3 = 2*10 / (2*3,14*20*0,000001) = 159,2 кОм

В схеме с одним операционным усилителем, желательно, чтобы коэффициент передачи не превышал 5 и добротность была не более 10. Для получения качественного фильтра параметры резисторов и конденсаторов должны как можно ближе соответствовать расчетным значениям.

Фильтр для нч динамика

Трёхполосные акустические системы, состоящие из трёх динамиков, являются самым удачным решением для высококачественного звуковоспроизведения. В них используются три типа звуковых головок. Они отличаются по размеру, конструктивным особенностям и полосе воспроизводимых частот. Для разделения всего частотного диапазона выдаваемого усилителем низкой частоты используются полосовые фильтры-кроссоверы. В них используются конденсаторы дроссели и, реже, резисторы.

Сделать своими руками фильтр для динамика НЧ очень просто.Основным элементом устройства является индуктивность или дроссель. Катушка включается последовательно с низкочастотным динамиком.

Re: Настройка фильтров акустических систем

Первый подход — выбирается точка в которой будет настраиваться ачх АС. Ставится в нее микрофон и снимаются АЧХ всех динамиков в корпусе АС. Загружаются в программу и согласуются АЧХ всех полос в одной точке. Очень быстрый и нетрудоемкий подход. Таких точек может быть напимер две. Однако равномерность АЧХ в других точках не гарантируется.

Второй подход более трудоемкий но дает более продвинутые результаты. АЧХ динамиков снимается на оси каждого из динамиков. Снимаются неосевые АЧХ(горизонтальные и вертикальные) каждого из динамиков. загружаются в программу именно измеренные осевые и неосевые АЧХ с указанием расположения динамиков. Расчет фильтра может проводиться для любой точки пространства охваченной полярными измерениями. На полярных графиках можно очень хорошо отследить все неравномерности АЧХ п пространстве. В этом отношении мне очень понравился LSPCAD 6,32. В нем есть поддержка файлов для ввода полярных измерений, а также полярные графики и Polar Map (непрерывныая цветная карта зависимноси давления от угла и частоты), и еще возможность отобразить на одном графике несколько АЧХ для разных углов. Этот подход более универсален однако более трудоемкий. Дает достаточно точное совпадение (расхождение не более 5%) расчетной АЧХ с измеренной для корпусов с неоч. сильной осевой ассимметрией. Для корпусов более сложной формы требуется кроме горизонтали и вертикали еще и промежуточные измерения.

Источник

Импедансная характеристика динамиков

Когда с примерными параметрами все более или менее ясно, самое время переходить к практике. Снимаем импедансную характеристику динамиков. С целью оценки сопротивления на графике имеется лесенка с шагом в один Ом. Скачек на 110 герцах это переключение с 10 Ом на 20.

Разумеется с такими горбами ни один фильтр нормально, и уж тем более расчетно работать не будет, особенно фильтр НЧ. Фильтру ВЧ этот подъем работать в общем то не мешает, однако как упоминалось ранее такой подъем на конце диапазона приведет к подъему высоких частот, в случае если усилитель имеет высокое сопротивление. Это можно использовать и во благо, оставив подъем небольшим.

Для примерного представления что от чего зависит привожу набор графиков для различных емкостей и сопротивлений. Ступенька начинается с 10 Ом.

Зная минимальное сопротивление НЧ звена, нужно привести к такому же и ВЧ звено. Тут много вариантов как соединить два резистора и цепочку Цобеля, и каждый кто решился на такой отважный шаг как сведение сам способен определить вид подключения и номиналы резисторов, поэтому описывать данную процедуру здесь излишне. Конкретно в данных колонках по результатам предварительного прослушивания решено было оставить родные резисторы на 2,2 ома и цепочку Цобеля параллельно ВЧ динамику.

Звук в конце тоннеля

Когда АвтоЗвук был еще маленьким и сидел под крылом Салона АВ, вышли в свет две первые части трилогии о сабвуферах — о том, чего ждать от разных типов акустического оформления и как подобрать динамик для закрытого ящика.

Значительная часть тех, кто, обдумывая житье, решил с пониманием отнестись к басовому вооружению своего автомобиля, этим, в принципе, уже могла бы обойтись. Но не все. Поскольку существует как минимум еще один, чрезвычайно популярный тип акустического оформления, по распространенности не уступающий закрытому ящику.

Фазоинвертор в отечественной литературе, bass reflex, ported box, vented box — в англоязычной — все это, по сути, звукотехническая реализация идеи резонатора Гельмгольца. Идея проста — замкнутый объем соединяется с окружающим пространством с помощью отверстия, содержащего некоторую массу воздуха. Вот именно существование этой массы — того самого столба воздуха, который, по утверждению Остапа Бендера, давит на любого трудящегося, и производит чудеса, когда резонатор Гельмгольца нанимают на работу в составе сабвуфера. Здесь мудреная вещь имени германского физика приобретает прозаическое имя тоннеля (по-буржуйски port или vent) .

Что такое фильтр?

Фильтр – это схема, которая удаляет или «отфильтровывает» определенный диапазон частотных компонентов. Другими словами, он разделяет спектр сигнала на частотные составляющие, которые будут передаваться дальше, и частотные составляющие, которые будут блокироваться.

Если у вас нет большого опыта анализа частотной области, вы можете быть не уверены в том, что представляют собой эти частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно. Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.

Давайте представим, что у нас есть аудиосигнал, который состоит из идеальной синусоидальной волны 5 кГц. Мы знаем, как выглядит синусоида во временной области, а в частотной области мы не увидим ничего, кроме частотного «всплеска» на 5 кГц. Теперь предположим, что мы включили генератор на 500 кГц, который вносит в аудиосигнал высокочастотный шум.

Сигнал, видимый на осциллографе, будет по-прежнему представлять собой только одну последовательность напряжений с одним значением на момент времени, но он будет выглядеть по-другому, поскольку его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокочастотные колебания шума.

Однако в частотной области синусоида и шум являются отдельными частотными компонентами, которые присутствуют одновременно в этом одном сигнале. Синусоидальная волна и шум занимают разные участки представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направив сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.

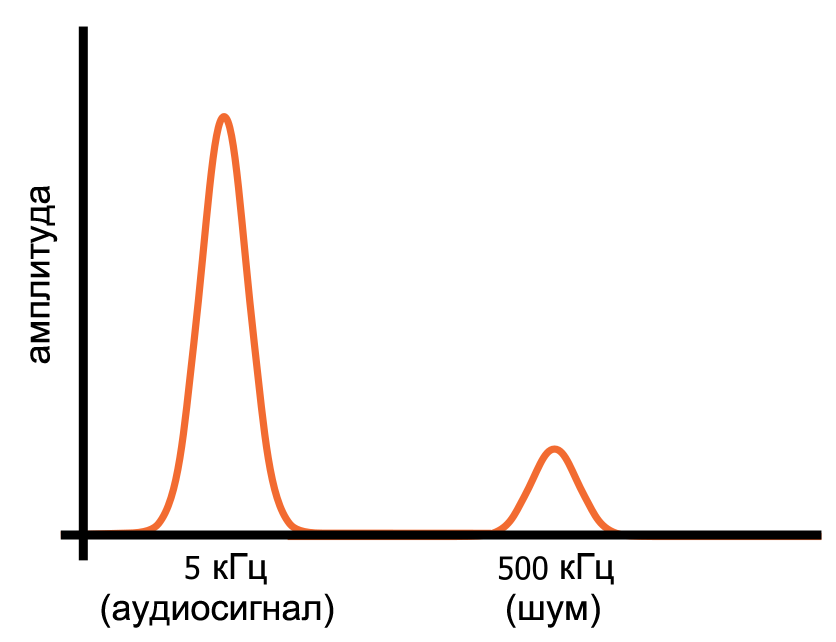Рисунок 3 – Представление аудиосигнала и высокочастотного шума в частотной области

Звучание системы

И конечно же надо сказать про звук. Стало лучше, сцена получилась очень недурственная. Кривизна АЧХ особо не слышна, даже наоборот, подъем на середине поддает детальности, верхов как ни странно хватает. Был замечен интересный эффект на басу. Как можно заметить по АЧХ на сотне герц большой подъем, а за ним завал, разумеется качающего баса нет, но есть мид бас. К примеру партия гитары кажется немного просаженным, а нижний бас, партия бас гитары, переходит как бы в слышимую область и читается очень четко, создается впечатление наличия того самого низкого баса.

Конечно ящики маловаты, и порой слышно подбубнивание, для устранения этого эффекта в каждую колонку было добавлено по 30 грамм натуральней шерсти. В целом данная акустика играет тепло и мягко даже без лампового усилителя, сохраняя в звуке строгость и точность камня, а вот с теплой лампой получается перебор мягкости. Все же им нужен усилитель по-строже — триод или двухтакт, но это тема для следующих экспериментов. Специально для сайта Радиосхемы — SecreTUseR.

Расчет lc фильтров

Порядок фильтра и его добротность

Подпишись на RSS!

Как рассчитать короб

Расчёт закрытого ящика

Расчёт фазоинвертора

Расчет амплитудно-частотной характеристики фильтра

Архивы

Определение частоты среза

Частота среза относительно амплитуды

Частота среза относительно сдвига фазы

Рис. 90. Схема бескаркасной намотки катушки

Фильтры Чебышева

Важные характеристики АС

Что такое полосовой фильтр

Важные характеристики АС

Расчет полосового фильтра

Пример упрощенного расчета элементов полосового фильтра на ОУ

Фильтр для нч динамика

Re: Настройка фильтров акустических систем

Импедансная характеристика динамиков

Звук в конце тоннеля

Что такое фильтр?

Звучание системы

Похожие записи: