важность
Постоянная Фарадея часто используется в расчетах в физике и химии , особенно в электрохимии . Это неизменная величина, т.е. естественная константа . Он используется, когда круговорот веществ связан с электрическими зарядами, например, при электролизе , например, в гальванике , или в топливных элементах и батареях
Поэтому это важно не только в науке , но и в технике , особенно в гальванике .
Он также используется для расчета изменения энергии, которое один моль электронов поглощает или выделяет при прохождении через (т. Е. Разность молярных энергий), и используется на практике для расчета общих параметров реакции, таких как преобразование электрические потенциалы в свободную энергию. Энергия 1 кДж / моль соответствует 1000 Дж / ( Н · А / моль -1 ), разбитому на одну частицу , и выражается в электрон-вольтах (эВ) с 1 эВ = 1 Дж · э / Кл. Результат:
- 1kJмОл знак равно^ 1000еVФ.(С.мОл-1)≈,01еV.{\ displaystyle 1 \; {\ frac {\ mathrm {kJ}} {\ mathrm {mol}}} \ \, \ mathrel {\ widehat {=}} \, \ {\ frac {1000 \; \ mathrm {эВ }} {F / (\ mathrm {C \, mol} ^ {- 1})}} \ приблизительно \, 0 {,} 01 \; \ mathrm {eV} \,.}
Понятие об электролитах
Прежде чем говорить об уравнении Фарадея, следует изучить свойства веществ, которые называют электролитами. Определение в химии для них дается простое: это любые соединения, раствор или расплав которых способен проводить электрический ток.
Для существования направленного движения зарядов внутри какой-либо субстанции необходимо выполнение двух обязательных условий:
- Наличие пространственной разницы потенциалов электрического поля внутри субстанции. Эта разница может создаваться за счет электрических батарей, например, внутри аккумуляторов. Ток должен быть постоянным, а не переменным.
- Существования свободных заряженных частиц. Если раствор или расплав являются нейтральными, то они образованы как положительными (катионы), так и отрицательными (анионы) частицами. Важным моментом является их способность свободно перемещаться внутри субстанции при приложении к ней некоторой разницы потенциалов.
Дело в том, что дистиллированная (абсолютно чистая) вода не проводит электричество, однако, уже незначительное количество примесей в ней делает ее хорошим проводником. Поскольку она также является замечательным растворителем благодаря полярному строению ее молекул, то часто применяется для приготовления растворов электролитов.
Способы определения ВТ при использовании импульсного тока
Если же через границу раздела фаз протекает импульсный ток, то при определении ВТ возникают большие трудности. Единой методики или прибора для определения ВТ при импульсномэлектролизе не существует. Сложность определения ВТ в условиях импульсногоэлектролиза обусловлена тем, что проходящий через систему ток расходуется не только на электрохимическую реакцию, но и на заряжение двойного электрического слоя. Электрический ток, проходящий через границу раздела и вызывающий электрохимическое превращение, называется часто фарадеевским током. Ток заряжения расходуется на заряжение двойного электрического слоя, реорганизацию растворителя, самого реагента, т.е. на все на то, что создает условия для протекания электрохимической реакции, поэтому выражение для общего тока, проходящего через электрохимическую систему, будет выглядеть следующим образом:
Второй закон
Фарадей, пропуская электрический ток одинаковой силы через различные электролиты, заметил, что массы веществ на электродах неодинаковы. Взвесив выделившиеся вещества, Фарадей сделал вывод, что вес зависит от химической природы вещества. Например, на каждый грамм выделенного водорода приходилось 107,9 г серебра, 31,8 г меди, 29,35 г никеля.
На основе полученных данных Фарадей вывел второй закон электролиза: для определённого количества электричества масса химического элемента, образовавшегося на электроде, прямо пропорциональна эквивалентной массе элемента. Она равна массе одного эквивалента – количеству вещества, реагирующему или замещающему 1 моль атомов водорода в химических реакциях:
μeq = μ/z,
где:
- μ – молярная масса вещества;
- z – число электронов на один ион (валентное число ионов).
Для выделения одного моля эквивалента затрачивается одинаковое количество электричества – 96485 Кл/моль. Это число называется числом Фарадея и обозначается буквой F.
Согласно второму закону, электрохимический эквивалент прямо пропорционален эквивалентной массе вещества:
k = (1/F) μeq или k = (1/zF)μ.

Рис. 3. Второй закон Фарадея.
Два закона Фарадея можно привести к общей формуле: m = (q / F) ∙ (μ/z).
ЭДС индукции. Закон электромагнитной индукции
Выше рассмотренные опыты показали, что в замкнутом контуре возникает индукционный ток при изменении магнитного потока, пронизывающего поверхность, ограниченную контуром. Как известно, ток в проводнике возникает в том случае, если на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного заряда вдоль замкнутого проводника называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в нем появляются сторонние силы (природу их выясним ниже: ЭДС индукции в движущихся проводниках), действие которых характеризуется ЭДС, называемой ЭДС индукции
Как показывает опыт, значение индукционного тока (а значит, и \(~\varepsilon_i\)) не зависит от причины изменения магнитного потока (изменяется ли площадь, ограниченная контуром, или его ориентация в пространстве, изменяется ли индукция магнитного поля при перемещении его источников или за счет изменения среды и т.д.). Существенное
значение имеет лишьскорость изменения магнитного потока \(~\frac {\Delta \Phi}{\Delta t}\) (так, стрелка гальванометра в опытах Фарадея отклоняется тем больше, чем быстрее вдвигается магнит в катушку). \(~ \mathcal h \varepsilon_i \mathcal i = -\frac {\Delta \Phi}{\Delta t}. \qquad (1)\) Эта формула выражает закон Фарадея для электромагнитной индукции:
среднее значение ЭДС индукции в проводящем контуре пропорционально скорости изменения магнитного потока через поверхность, ограничен ную контуром. Мгновенное значение ЭДС индукции равно взятой с противоположным знаком первой производной от магнитного потока по времени, т.е.
\(~\mathcal h \varepsilon_i \mathcal i = {\Phi}'(t)\).
Советуем изучить Варианты подсветки потолка в помещениях
Знак «-» учитывает правило Ленца, согласно которому при увеличении магнитного потока \(~(\frac {\Delta \Phi}{\Delta t} > 0)\) ЭДС индукции отрицательная \(~(\varepsilon_i 0)\).
Сила индукционного тока в замкнутом контуре рассчитывается по закону Ома\ где R
— сопротивление контура.
Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в переменное магнитное поле. В соответствии с законом электромагнитной индукции любые изменения магнитного потока, пронизывающего проводящее тело, сопровождаются возникновением в нем индукционных токов. Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми (а также токами Фуко)
. Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего вихревые токи. Токи Фуко можно обнаружить на опыте с маятником (проводящей пластиной), колеблющемся в зазоре между полюсами электромагнита. До включения маятник совершает практически незатухающие колебания. При пропускании тока через катушку электромагнита маятник испытывает сильное торможение и очень быстро останавливается. Торможение маятника объясняется действием магнитного поля на индукционные токи, возникающие в пластине при ее движении в магнитном поле. Если в пластине сделать разрезы, то вихревые токи ослабляются и торможение почти отсутствует. Этот факт торможения используется для успокоения подвижных частей различных приборов.
Токи Фуко вызывают нагревание проводников (якоря генераторов и сердечников трансформаторов), выделяемая токами Фуко теплота используется в индукционных металлургических печах и в других случаях.
По закону Фарадея (1) определяется ЭДС индукции, возникающая и в движущемся проводнике, и в неподвижном (см. опыты, описанные в разделе Электромагнитная индукция). Но механизм происхождения ЭДС индукции в этих случаях различен.
Электролиз. Законы Фарадея
Электролизом называют процессы, протекающие на электродах под действием электрического тока, подаваемого от внешнего источника тока через электролиты.
При электролизе на электродах непрерывно протекают окислительно-восстановительные реакции. На катоде (К(-)) происходит процесс восстановления, на аноде (А(+)) – процесс окисления. Продукты этих реакций или откладываются на электродах, или вступают во вторичные реакции (взаимодействуют между собой, с молекулами растворителя или с веществом электрода), или накапливаются в растворе у электродов. Течение первичных анодных и катодных реакций подчиняется законам Фарадея.
Первый закон Фарадея: масса вещества m, выделяемая на электроде электрическим током, пропорциональная количеству электричества Q, прошедшему через электролит:
m = kQ, но Q =It (9.16)
где I – сила тока, А; t – время пропускание тока, с.
m = kIt (9.17)
k – коэффициент пропорциональности, равный количеству вещества, выделяемого при прохождении одного кулона (Кл) электричества (электрохимический эквивалент).
Второй закон Фарадея: массы различных веществ, выделенных одним и тем же количеством электричества, пропорциональных их химическим эквивалентам (Мэ):
Для выделения 1 грамма эквивалента вещества требуется пропустить через электролит одно и тоже количество электричества, равное приблизительно 96500 Кл (число Фарадея). Следовательно:
Подставив последнее уравнение в (9.17), получим формулу, объединяющую оба закона Фарадея.
(9.18)
Соотношение (9.18) используют в расчетах процессов при электролизе. При практическом проведении электролиза всегда некоторая часть электрической энергии затрачивается на побочные процессы
Важной характеристикой рентабельности установки для проведения электролиза (электролизера) является выход по току (h, %):
h = (9.19)
где mпр – масса фактически выделенного вещества; mтеор – масса вещества, которая должна была выделиться в соответствии с законом Фарадея.
На процесс электролиза существенно влияет плотность тока, то есть сила тока, приходящаяся на единицу рабочей поверхности электрода.
Рассмотрим процессы, протекающие на катоде и аноде. Если электролиз идет в расплаве соли, то на катоде выделяется металл, а на аноде газ аниона.
Например, электролиз расплава хлорида натрия приводит к восстановлению ионов Na+ до металлического натрия на катоде (отрицательном электроде)
Na+ + 1e Na
и окислению хлорид ионов Cl– до газообразного хлора на аноде (положительном электроде)
Cl– – e 1/2 Cl2.
Суммарная реакция:
NaClNa + 1/2 Cl2.
Если электролиз идет в растворе соли, то помимо катиона металла и аниона в растворе находятся ионы H+ и OH+:
H2O D H++OH-.
При наличии нескольких видов ионов или недиссоциированных молекул электрохимически активных веществ возможно протекание нескольких электродных реакций. На катоде, прежде всего, протекает реакция с наиболее положительным потенциалом. Поэтому при катодном восстановлении возможно три случая:
Катионы металлов, стоящие в ряду напряжения от Li+ до Al3+ включительно не восстанавливаются на катоде, вместо них выделяется водород:
2Н2О + 2e Н2 + 2OH-;
Катионы металлов, находящиеся в ряду напряжения от Al3+ до H+ (включительно) восстанавливаются одновременно с молекулами воды, что связано с более высокой поляризацией (перенапряжением) при выделении водорода, чем поляризацией (перенапряжением) разряда многих металлов:
Меn+ + ne Ме°
2Н2О + 2e Н2 + 2ОН-
Катионы металлов, стоящие в ряду напряжения после водорода полностью восстанавливаются на катоде:
Меn+ + ne Ме°.
На аноде в первую очередь реагируют наиболее сильные восстановители – вещества, имеющие наиболее отрицательные потенциалы.
На нерастворимом аноде (уголь, графит, платина, иридий) анионы кислородсодержащих кислот не окисляются, а окисляется вода с образованием кислорода:
2Н2О – 4e 4Н+ + О2.
Анионы бескислородных кислот (Cl-, I-, Br-, S2- и т.д.) окисляются до простых веществ (Cl2, I2, Br2, S и т. д.) при высокой плотности тока. При малой плотности тока выделяется только кислород, а при выравнивании потенциала и протекают обе реакции.
На растворимом аноде идет процесс растворения самого анода, например, Сu +- 2e Cu2+.
Электролиз применяют в:
1) металлургии для получения меди, цинка, кобальта, марганца и других металлов;
2) в химической промышленности электролизом получают газообразный хлор, водород, кислород, щелочи, окислители (пероксид водорода, перманганат калия, хлораты и другие);
3) получение гальванопокрытий: никелирование, меднение, цинкование, хромирование;
4) электрохимическая анодная обработка металлов и сплавов для придания изделиям определенной формы.
Литература
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.344- 351.
- Жилко В.В. Физика: учеб. пособие для 11-го кл. общеобразоват. учрежде-ний с рус. яз. Обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В.В. Жилко, Л.Г. Маркович. — Мн.: Нар. асвета, 2008. — С. 170-182.
- Мякишев, Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. — М.: Дрофа, 2005. — С. 399-408, 412-414.
Майкл Фарадей – основоположник закона индукции
Ученый занимавшиеся изучением электричества – великий английский физик и химик Майкл Фарадей (1791-1867). Его заслуга в изучении взаимной магнитной индукции между двумя связанными контурами как основа при производстве электричества огромна.
Будучи сыном кузнеца, он был самоучкой, благодаря книгам по химии и электричеству, которые он читал во время своего ученичества в переплетной мастерской—работу, которую он начал в возрасте 14 лет. Когда он был еще подростком, у него была возможность посещать лекции великого химика Хамфри Дэви в Королевском институте. В возрасте 21 года Дэви нанял его помощником в Королевский институт, где Фарадей оставался в течение следующих 50 лет, будучи назначен заведующим его лабораторией в 1821 году. Хотя отсутствие формального образования оставляло ему математические пробелы, они были в значительной степени компенсированы поразительной экспериментальной интуицией, которая позволила ему стать одним из самых влиятельных экспериментальных исследователей всех времен.
В 1821 году Фарадей начал исследовать взаимодействие между магнитами и токами. Он разработал концепцию силовой линии (термин, который он ввел) для обоснования фигур, образованных железными опилками вблизи магнита. Используя эту концепцию, в августе 1831 года он открыл взаимную магнитную индукцию, отметив переходный ток, индуцируемый в катушке, когда ток включался и выключался во второй катушке. Обе катушки были намотаны на один и тот же тороидальный железный сердечник.
В октябре 1831 года Фарадей наблюдал самоиндукцию, возникающую в результате тока, индуцируемого в соленоидальной катушке движением магнита внутри ее отверстия.
Фарадей ввел термин электродвижущая сила для такого эффекта, и мы все еще видим это в использовании сегодня.
В 1831 году Фарадей также создал представление электромеханического генератора. Он ввел понятие диэлектрической проницаемости и построил первый переменный конденсатор в 1837 году. Он также изучал оптику и поляризацию света вместе со своим другом Чарльзом Уитстоуном, открыв в 1845 году эффект Фарадея (вращение поляризованного света при прохождении через намагниченную область).
Между 1846 и 1855 годами Фарадей признал магнитные свойства материи и ввел понятие диамагнетизма. Развивая идею силовых линий, он ввел понятия электрического и магнитного полей.
Не менее важными были открытия Фарадея в области химии, где он написал несколько прорывных работ. Он собрал свою колоссальную научную продукцию главным образом в экспериментальных исследованиях, опубликованных в нескольких номерах между 1839 и 1855 годами. Он выступал с памятными лекциями в Королевском институте, был назначен членом Королевского общества в 1824 году и дважды получил медаль Копли, в 1832 и 1838 годах, но отказался от дворянского титула и президентства Королевского института (1864) и не хотел регистрировать никаких патентов.
Закон Максвелла
В 1873 году Джон Максвелл теоретически изложил действие электромагнитного поля. Его уравнения составили основу для создания электротехники. Уравнения, полученные им устанавливают взаимосвязь магнитных явлений с электрическими и наоборот. Вместе с тем физик обнаружил, что значение распространения электромагнитной волны совпадает со скоростью света.
Физический смысл уравнений заключается в следующем:
- изменение электрического поля приводит к возникновению магнитного: Edl = -dФ/dt;
- если существует магнитное поле, то оно вызывает появление электрического: Hdl = -dN/dt.

В формулах: E — это напряжение электрополя на участке цепи; H — напряжённость; N — поток индукции; t — время. В том случае, когда контур замкнут при изменении магнитного потока возникает электродвижущая сила (ЭДС). Проявляется она в виде индукционного тока: I = e * i / R, где R — сопротивление цепи. Если контур будет незамкнутым, то в месте обрыва возникнет разность потенциалов.
Направление движения индукционного тока определяется по правилу Ленца. Формулироваться оно будет так: возникающее движение носителей зарядов направлено таким образом, чтобы магнитное поле противодействовало потоку им вызывающимся. На практике же сторону движения индукционного тока можно определить следующим образом:
- выяснить направление внешнего магнитного поля;
- узнать возрастает или спадает поток вектора магнитной индукции;
- используя правило Ленца, определить направление вектора;
- воспользовавшись методом правого винта найти направление индукционного тока в контуре.
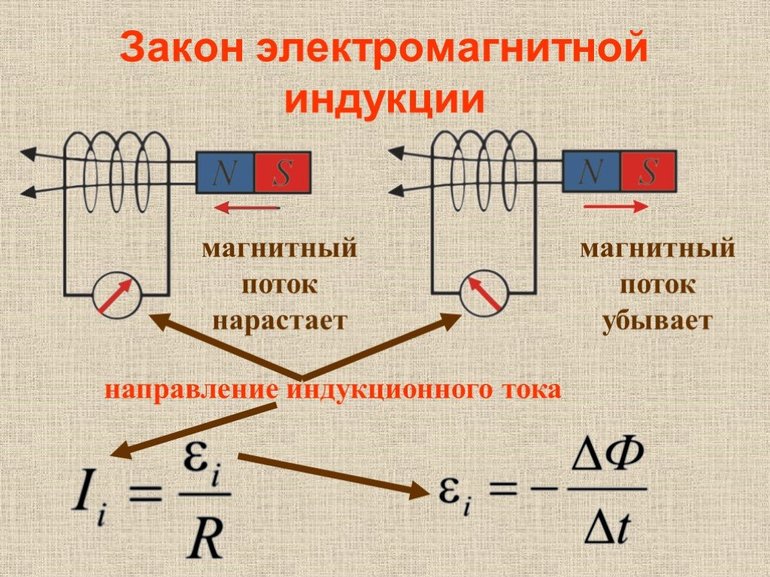
Таким образом, если имеется N витков в контуре, то сила индукции равна: E = — N * (dФ / dt). Отсюда сила тока в цепи будет следующей: I = E / R. Если же длина проводника равна L, а скорость V, то в однородном постоянном поле электромагнитную индукцию (ЭМИ) можно найти как E = B * V * L * sin (a), где альфа-угол между векторами.
Кратко объяснить природу ЭДС самоиндукции можно так. Пусть имеется проводник длиной L вокруг которого изменяется магнитное поле со скоростью V. На заряд двигающийся под действием намагниченности оказывает влияние сила Лоренца: F = q * (E + v * B). Отрицательные заряды собираются возле одного края проводника, а некомпенсированные положительные у другого. В итоге возникает напряжение. Представляет оно собой ЭДС индукции (e * i). Найти её значение можно, определив работу, которая совершается силой Лоренца при движении заряда по проводнику: ei = A / q = F * L / q = B·V·L·sin (a).
https://youtube.com/watch?v=2vGT5YlCEtk
Фарад
| фарад | |
| Ф, F | |
| Величина | электрическая ёмкость |
| Система | СИ |
| Тип | производная |
Фара́д
(русское обозначение:Ф ; международное обозначение:F ; прежнее название —фара́да ) — единица измерения электрической ёмкости в Международной системе единиц (СИ), названная в честь английского физика Майкла Фарадея . 1 фарад равен ёмкости конденсатора, при которой заряд 1 кулон создаёт между его обкладками напряжение 1 вольт :
Через основные единицы системы СИ фарад выражается следующим образом:
В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы «фарад» пишется со строчной буквы, а её обозначение — с заглавной (Ф). Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием фарада. Например, обозначение единицы измерения абсолютной диэлектрической проницаемости «фарад на метр» записывается как Ф/м.
В Международную систему единиц фарад введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом .
Фарад — очень большая ёмкость для уединённого проводника: ёмкостью 1 Ф обладал бы уединённый металлический шар, радиус которого равен 13 радиусам Солнца (ёмкость же шара размером с Землю, используемого как уединённый проводник, составляла бы около 710 микрофарад).
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
- µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
- N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.
Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
- l — длина проводника в метрах;
- r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Tags: , ампер, бра, буравчик, вид, вред, генератор, двигатель, дом, , знак, измерение, как, компьютер, конструкция, контур, , магнит, магнитный, паровой, постоянный, потенциал, правило, принцип, провод, , работа, размер, ряд, самоиндукция, сопротивление, схема, тен, ток, трансформатор, , эффект
§ 35. Электрический ток в электролитах
Закон электролиза Фарадея. Закон электролиза был экспериментально установлен Фарадеем в 1833 г.
Масса m вещества, выделившегося на электроде, прямо пропорциональна электрическому заряду q, прошедшему через электролит:
m = kq.
(1)
В формуле (1) коэффициент пропорциональности k называют электрохимическим эквивалентом данного вещества. Он численно равен массе вещества, выделившегося на одном из электродов при прохождении через электролит единичного электрического заряда. В СИ электрохимический эквивалент измеряют в килограммах на кулон . Значения электрохимических эквивалентов некоторых веществ приведены в таблице.
| Вещество | k, 10-8 | Вещество | k, 10-8 |
| Алюминий | 9,32 | Никель (двухвалентный) | 30,4 |
| Водород | 1,04 | Никель (трёхвалентный) | 20,3 |
| Кислород | 8,29 | Хлор | 36,7 |
| Медь (одновалентная) | 65,9 | Хлом | 18,0 |
| Медь (двухвалентная) | 32,9 | Цинк | 33,9 |
Поскольку q = It, где I — сила тока, t — промежуток времени прохождения тока через электролит, то
m = kIt.
От теории к практике
Никелирование изделия двухвалентным никелем осуществлялось в течение промежутка времени t = 20 мин при силе тока I = 15 А. Определите массу слоя никеля, осаждённого на изделии.
Массу m вещества, выделившегося на электроде при прохождении через электролит электрического заряда q, можно определить, зная массу m одного иона и число N осевших на этом электроде ионов:
, ,
где M — молярная масса выделившегося вещества, NА — постоянная Авогадро.
Тогда число ионов: .
С другой стороны, число ионов, нейтрализовавшихся на электроде:
где q — заряд одного иона. Так как заряд иона q кратен элементарному заряду e, то q = en, где n — валентность иона.
Значит, и
(2)
Сравнивая формулы (2) и (1), получим
(3)
Так как NА и е – универсальные постоянные, то физическую величину в честь М. Фарадея назвали постоянной Фарадея.
С учётом этого формулу (3) для определения электрохимического эквивалента вещества можно записать в виде:
Используя закон электролиза, можно определить значение заряда электрона в школьной лаборатории. Допустим, что I — сила тока, который проходил через электролит в течение промежутка времени t (можно измерить амперметром). При этом на электроде выделилось вещество, масса которого m (можно измерить, взвесив электрод до и после прохождения тока через электролит). Тогда модуль заряда электрона определяют по формуле.
Первый закон Фарадея
Данный закон был выведен ученым экспериментальным путем. Он определяет пропорциональную зависимость между массой вещества, образующегося на электроде и зарядом, проходящим через электролитический раствор.
Эту пропорцию наглядно отображает формула m=k х Q=k х I х t, где k является коэффициентом пропорциональности или электрохимическим эквивалентом, Q – заряд, прошедший через электролит, t – время прохождения заряда, m – масса вещества, образовавшегося на электроде в результате реакции.
Первый закон Фарадея служит для определения количества первичных продуктов, образовавшихся в процессе электролиза на электродах. Масса этого вещества составляет суммарную массу всех ионов, попавших на электрод. Это подтверждается формулой m=m0 х N = m0 х Qq0 = m0q0 х I х t, в которой m0 и q0 соответственно являются массой и зарядом единичного иона. N=Qq0 – определяет количество ионов, попавших на электрод за время прохождения заряда Q через раствор электролита.
Следовательно, величина электрохимического эквивалента k представляет собой соотношение массы иона m0 используемого вещества и заряда q0 этого иона. Известно, что величина заряда иона составляет произведение валентности n этого вещества и элементарного заряда е, то есть, q0 = n х e. Исходя из этого, электрохимический эквивалент k будет выглядеть следующим образом: k = m0q0 = m0 х NAn х e х NA = 1F х μn. В этой формуле NA является постоянной Авогадро, μ – молярной массой данного вещества. F = e х NA является постоянной Фарадея и составляет 96485 Кл/моль.
Числовое значение данной величины равняется заряду, который должен быть пропущен через раствор электролита, для того чтобы на электроде выделился 1 моль вещества с одинаковой валентностью. Рассматриваемый закон Фарадея для электролиза примет вид еще одной формулы: m = 1F х μn х I х t.
Источник
Ценность и единство
Он рассчитывается из постоянной Авогадро и элементарного заряда:
NА.{\ Displaystyle N _ {\ mathrm {A}}} е{\ displaystyle e}
- Ф.знак равноNА.⋅е{\ Displaystyle F = N _ {\ mathrm {A}} \ cdot e}
и имеет значение:
- Ф.знак равно6.02214076⋅10231мОл⋅1,602176634⋅10-19-еС.знак равно96485,3321233100184С.мОл{\ displaystyle F = 6 {,} 022 \, 140 \, 76 \ cdot 10 ^ {23} {\ frac {\ mathrm {1}} {\ mathrm {mol}}} \ cdot 1 {,} 602 \, 176 \, 634 \ cdot 10 ^ {- 19} {\ mathrm {C}} = 96 \, 485 {,} 332 \, 123 \, 310 \, 0184 \, {\ frac {\ mathrm {C}} { \ mathrm {mol}}}}.
В системе единиц СИ Моль и кулоновское определены в том , что константа и точные численные значения . Это означает, что значение также можно указать точно.
NА.{\ Displaystyle N _ {\ mathrm {A}}}е{\ displaystyle e}Ф.{\ displaystyle F}
Причины возникновения индукционного тока в движущихся и неподвижных проводниках
Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:
- Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
- Изменение магнитного поля при неподвижном контуре.
Перейдем к рассмотрению этих случаев подробнее.
Перемещение контура или его частей в неизменном магнитном поле
При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.
Пример 2
На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.
Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон
На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:
FЛ=eυ→B.
Работа силы FЛ на пути l равна:
A=FЛ·l=eυBl.
По определению ЭДС:
δинд=Ae=υBl.
Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.
Следовательно,
δинд=∆Φ∆t.
Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.
При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:
∆Q=RIинд2∆t=υ2B2l2R∆t
Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.
Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:
Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t
Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.
Изменение магнитного поля при неподвижном контуре
Определение 3
Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.
В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.
В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.
Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.
Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Рисунок 1.20.4. Модель электромагнитной индукции
Рисунок 1.20.5. Модель опытов Фарадея
Рисунок 1.20.6. Модель генератора переменного тока
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Энергия магнитного поля
Вспомним второй опыт с лампочкой, которая не горит при замкнутом ключе и ярко вспыхивает при размыкании цепи. Мы непосредственно наблюдаем, что после размыкания ключа в лампочке выделяется энергия. Но откуда эта энергия берётся?
Берётся она, ясное дело, из катушки — больше неоткуда. Но что за энергия была запасена в катушке и как вычислить эту энергию? Чтобы понять это, продолжим нашу электромеханическую аналогию между индуктивностью и массой.
Чтобы разогнать тело массы из состояния покоя до скорости , внешняя сила должна совершить работу . Тело приобретает кинетическую энергию, которая равна затраченной работе: .
Чтобы после замыкания цепи ток в катушке индуктивности достиг величины , источник тока должен совершить работу по преодолению вихревого электрического поля, направленного против тока. Работа источника идёт на создание тока и превращается в энергию магнитного поля созданного тока. Эта энергия запасается в катушке; именно эта энергия и выделяется потом в лампочке после размыкания ключа (во втором опыте).
Индуктивность служит аналогом массы ; сила тока является очевидным аналогом скорости . Поэтому естественно предположить, что для энергии магнитного поля катушки может иметь место формула, аналогичная выражению для кинетической энергии:
(3)
(тем более, что правая часть данной формулы имеет размерность энергии — проверьте!).
Формула (3) действительно оказывается справедливой. Уметь её выводить пока не обязательно, но если вы знаете, что такое интеграл, то вам не составит труда понять следующие рассуждения.
Пусть в данный момент сила тока через катушку равна . Возьмём малый промежуток времени . В течение этого промежутка приращение силы тока равно ; величина считается настолько малой, что много меньше, чем .
За время по цепи проходит заряд . Вихревое электрическое поле совершает при этом отрицательную работу:
Источник тока совершает такую же по модулю положительную работу (сопротивлением катушки, напомним, мы пренебрегаем, так что вся работа источника совершается против вихревого поля):
Интегрируя это от нуля до , найдем работу источника , которая затрачивается на создание тока :