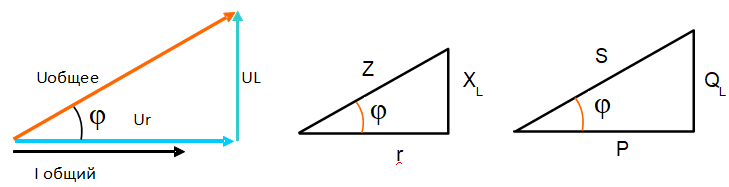Расчет индуктивности катушек: формула

§ 2.9. Закон Ома для электрической цепи переменного тока

Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С (рис. 2.20).

Рис. 2.20

Чему равна амплитуда силы тока в такой цепи (колебательном контуре), если на ее концах поддерживается напряжение u(t) = U sin ωt?

Мы видели, что при включении по отдельности в цепь проводника с активным сопротивлением R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами (2.6.2), (2.7.3) и (2.8.4). Амплитуды же напряжений на резисторе, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так:

В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи переменного тока, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.

Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.

Действительно, квазистационарный ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлением. Однако только на участке с активным сопротивлением колебания напряжения и силы тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний силы тока на π/2 (см. § 2.7), а на катушке индуктивности колебания напряжения опережают колебания силы тока на π/2 (см. § 2.8).

Векторная диаграмма электрической цепи

Для вывода закона Ома в случае электрической цепи переменного тока, изображенной на рисунке 2.20, нужно уметь складывать мгновенные колебания напряжений, сдвинутых по фазе друг относительно друга. Проще всего выполнять сложение нескольких гармонических колебаний с помощью векторных диаграмм, о которых было рассказано в § 1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду силы тока в зависимости от амплитуды напряжения и сдвиг фаз между силой тока и напряжением.

Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока _m. Этот вектор изобразим в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с силой тока. Поэтому вектор _mR должен совпадать по направлению с вектором _m. Его модуль равен U_mR = I_mR.

Рис. 2.21

Колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2 и соответствующий вектор и _mL должен быть повернут относительно вектора _m на π/2. Его модуль равен U_mL = IωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор _mL следует повернуть налево на π/2. (Можно было бы, конечно, поступить и наоборот.)

Вектор напряжения на конденсаторе _mC отстает по фазе от вектора _m на π/2 и поэтому повернут на этот угол относительно вектора _m направо. Его модуль равен .

Для нахождения вектора суммарного напряжения _m нужно сложить три вектора: _mR, _mL и _mC. Вначале удобнее сложить два вектора _mL и _mC (рис. 2.22).

Рис. 2.22

Модуль этой суммы равен , если . Именно такой случай изображен на рисунке. После этого, сложив вектор _mL + _mC с вектором _mR, получим вектор _m, характеризующий колебания напряжения в сети.

По теореме Пифагора (из треугольника АОВ):

или

Из равенства (2.9.2) можно найти амплитуду силы тока в цепи:

Это и есть закон Ома для электрической цепи переменного тока, изображенной на рисунке 2.20.

Благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи (см. рис. 2.20) выражается так:

От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин. Они связаны друг с другом точно так же, как и амплитуды в формуле (2.9.3):

Мгновенное значение силы тока меняется со временем гармонически:

где φ_c, — разность фаз между силой тока и напряжением в сети. Она зависит от частоты со и параметров цепи R, L, С.

Сдвиг фаз между током и напряжением

Сдвиг фаз φ_c, между колебаниями силы тока и напряжения равен по модулю углу φ между векторами _m и _m (см. рис. 2.22). Как следует из этого рисунка,

Согласно рисунку 2.22, сила тока отстает от напряжения по фазе при условии . Поэтому сдвиг фаз φ_c = -φ и

В частных случаях цепей с активным, емкостным и индуктивным сопротивлениями из этой формулы получаются правильные значения сдвига фаз.

Что такое индуктивность

Индуктивностью называется идеализированный элемент электрической цепи, в котором происходит запасание энергии магнитного поля. Запасания энергии электрического поля или преобразования электрической энергии в другие виды энергии в ней не происходит.

Наиболее близким к идеализированному элементу — индуктивности — является реальный элемент электрической цепи — индуктивная катушка.

В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электрического поля и преобразование электрической энергии в другие виды энергии, в частности в тепловую.

Количественно способность реального и идеализированного элементов электрической цепи запасать энергию магнитного поля характеризуется параметром, называемым индуктивностью.

Таким образом термин «индуктивность» применяется как название идеализированного элемента электрической цепи, как название параметра, количественно характеризующего свойства этого элемента, и как название основного параметра индуктивной катушки.

Рис. 1. Условное графическое обозначение индуктивности

Связь между напряжением и током в индуктивной катушке определяется законом электромагнитной индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости изменения потокосцепления катушки ψ и направленная таким образом, чтобы вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:

Потокосцепление катушки равно алгебраической сумме магнитных потоков пронизывающих ее отдельные витки:

где N — число витков катушки.

В системе единиц СИ магнитный поток и потокосцепление выражают в веберах (Вб).

Магнитный поток Ф, пронизывающий каждый из витков катушки, в общем случае может содержать две составляющие: магнитный поток самоиндукции Фси и магнитный поток внешних полей Фвп: Ф — Фси + Фвп.

Первая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током, вторая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и постоянных магнитов. Если вторая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее называют магнитным потоком взаимоиндукции.

Потокосцепление катушки ψ , так же как и магнитный поток Ф, может быть представлено в виде суммы двух составляющих: потокосцепления самоиндукции ψси , и потокосцепления внешних полей ψ вп

Наведенная в индуктивной катушке ЭДС е, в свою очередь, может быть представлена в виде суммы ЭДС самоиндукции, которая вызвана изменением магнитного потока самоиндукции, и ЭДС, вызванной изменением магнитного потока внешних по отношению к катушке полей:

здесь еси — ЭДС самоиндукции, евп — ЭДС внешних полей.

Если магнитные потоки внешних по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только ЭДС самоиндукции.

Потокосцепление самоиндукции зависит от протекающего по катушке тока. Эта зависимость, называемая вебер — амперной характеристикой индуктивной катушки, в общем случае имеет нелинейный характер (рис. 2, кривая 1 ).

В частном случае, например для катушки без магнитного сердечника, эта зависимость может быть линейной (рис. 2, кривая 2).

Рис. 2. Вебер-амперные характеристики индуктивной катушки: 1 — нелинейная, 2 — линейная.

В системе единиц СИ индуктивность выражают в генри (Гн).

При анализе цепей обычно рассматривают не значение ЭДС, наведенной в катушке, а напряжением на ее зажимах, положительное направление которого выбирают совпадающим с положительным направлением тока:

Идеализированный элемент электрической цепи — индуктивность, можно рассматривать как упрощенную модель индуктивной катушки, отражающую способность катушки запасать энергию магнитного поля .

Для линейной индуктивности напряжение на ее зажимах пропорционально скорости изменения тока. При протекании через индуктивность постоянного тока напряжение на ее зажимах равно нулю, следовательно, сопротивление индуктивности постоянному току равно нулю.

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

https://youtube.com/watch?v=aGZ3H7s_zMI

Конструкция катушки

По конструктивному исполнению индуктивные элементы различаются:

• видом намотки: винтоспиральная, винтовая; кольцевая;
• количеством слоёв: однослойные или многослойные;
• типом изолированного провода: одножильный, многожильный;
• наличием каркаса: каркасные или бескаркасные (при небольшом количестве витков толстого провода);
• геометрией каркаса: прямоугольный, квадратный, тороидальный;
• наличием сердечника: ферритовый, из карбонильного железа, электротехнической стали, пермаллоевый (магнитомягкий сплав), металлический (латунный);
• геометрией сердечника: стержневой (разомкнутый), кольцо-образный или ш-образный (замкнутый);
• возможностью изменять L в узких интервалах (движение сердечника по отношению к обмотке).

Индуктивность проводника

Существуют плоские катушки, в печатном исполнении устанавливаемые на платах цифровых устройств.

К сведению. Намотка провода может быть как рядовой (витком к витку), так и в навал. Последний способ укладки провода снижает паразитную ёмкость.

Конструкция катушек

Постоянный и переменный

Сила тока и напряжение могут быть как постоянными, так и переменными. Постоянство величины говорит о ее неизменности во времени. Напротив, переменные величины периодически изменяют свое значение во времени. Если напряжение питания окажется переменным, то и сила тока, генерируемая им, будет переменной величиной. Это значит, что оба этих значения будут то увеличиваться, то уменьшаться. Форма сигнала может быть различной:

• Синусоидальный сигнал (плавное возрастание — убывание).
• Меандр (прямоугольный, треугольный сигнал), когда значение резко претерпевает изменение.
• Пульсирующий сигнал, изменяющийся то плавно, то резко, согласно некоторому закону.

Вне зависимости от того, постоянным или переменным является ток, его главное отличие от напряжения — то, что ток — это движение носителей заряда, а напряжение — причина этого движения.

Советуем изучить — Принцип работы токовой направленной защиты нулевой последовательности в электрических сетях 110 кВ

Расчет параметров катушки

Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.

Расчет L в зависимости от заданной конструкции

Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:

L = 0,01*D*w2/(l/D) + 0,46,

где:

• D – диаметр каркаса, см;
• w – число витков;
• l – длина намотки, см;
• L – индуктивность, мкГн.

Подставляя численные значения в формулу, получают значение L.

Расчет количества витков по индуктивности

Зная D каркаса и L, рассчитывают количество витков в катушке, формула имеет вид:

где:

• L – индуктивность, мкГн;
• D – диаметр каркаса, мм.

Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:

Расчет параметров катушки

Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.

Расчет L в зависимости от заданной конструкции

Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:

L = 0,01*D*w2/(l/D) + 0,46,

где:

• D – диаметр каркаса, см;
• w – число витков;
• l – длина намотки, см;
• L – индуктивность, мкГн.

Подставляя численные значения в формулу, получают значение L.

Расчет количества витков по индуктивности

Зная D каркаса и L, рассчитывают количество витков в катушке, формула имеет вид:

w = 32*√(L*D),

где:

• L – индуктивность, мкГн;
• D – диаметр каркаса, мм.

Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:

w = l/d,

где:

• l – длина намотки, мм;
• d – диаметр провода, мм.

Измерения диаметра провода проводят линейкой или штангенциркулем.

Расчёт индуктивности прямого провода

Собираясь найти L круглого прямого проводника, обращаются к приближённой формуле:

L = (μ0/2π)*l*( μe*ln(l/r) + 1/4* μi,

где:

• μ0 – магнитная постоянная;
• μe – относительная магнитная проницаемость (ОМП) среды (для вакуума – 1);
• μi – ОМП проводника;
• l – длина провода;
• r – радиус провода.

Формула справедлива для длинного проводника.

Расчёт однослойной намотки

Однослойные дроссели без сердечника легко и быстро можно рассчитать при помощи онлайн-калькулятора, в окно которого можно забить все известные характеристики, и программа выдаст значение L.

Вычисления проводятся и вручную, с использованием математического выражения. Оно имеет вид:

L = D2*n2/45D + 100*l,

где:

• D – диаметр катушки, см;
• l – длина намотанного провода, см;
• n – количество витков.

Формула подходит для вычислений L дросселей без ферритовых сердечников.

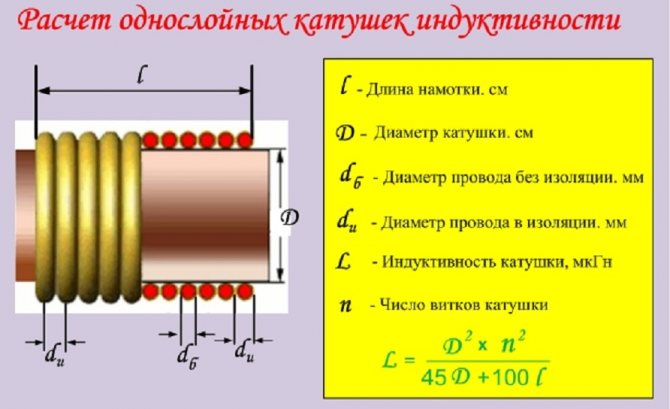
Однослойная катушка виток к витку

Дроссель с сердечником

При наличии сердечника следует учесть его размеры и форму. В случае одинаковых катушках индуктивность больше у той, которая располагается на сердечнике.

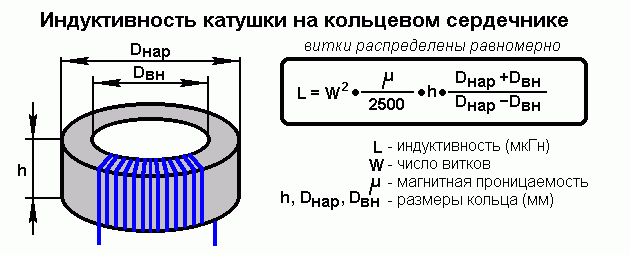
Расчёт однослойной намотки с сердечником

Многослойная намотка

Особенности расчёта при подобном способе наматывания провода заключаются в том, что нужно учитывать его толщину. Формула для дросселя без сердечника имеет вид:

N²=(L*(3Dk+9l+10t))/0.008Dk²,

где:

• Dk – общий диаметр (диаметр каркаса и намотки);
• t – толщина слоя;
• l – длина накрученного провода.

Все значения подставляют в мм, величину L – в мкГн.

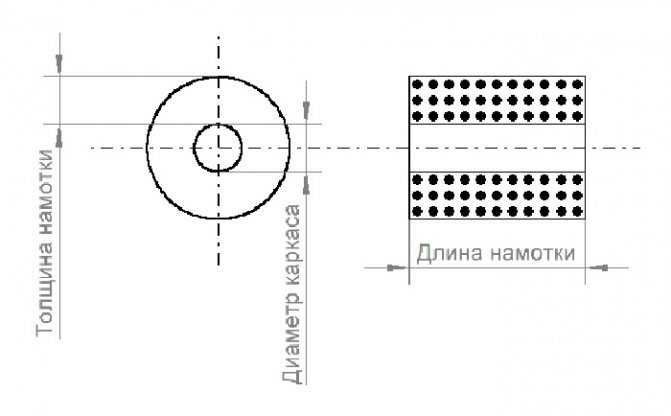
Многослойная намотка

Конструкция

Главное назначение катушек индуктивности ГОСТ 20718-75 – это накопление электрической энергии в пределах магнитного поля для акустики, трансформаторов и т. д. Их используют для разработки и конструирования различных селективных схем и электрических устройств. От конструкции (материала, количества витков), наличия каркаса зависит их функциональность, размеры и область использования. Изготовление устройств производится на заводах, но можно сделать их самостоятельно. Самодельные элементы несколько уступают по надежности профессиональным, но обходятся в разы дешевле.

Фото — схема

Каркас катушки индуктивности выполняется из диэлектрического материала. На него наматывается изолированный проводник, который может быть как одножильным, так и многожильным. В зависимости от типа намотки, они бывают:

1. Спиральными (на ферритовом кольце);
2. Винтовыми;
3. Винтоспиральными или комбинированными.

Примечательной особенностью катушки индуктивности для электрических схем является то, что её можно намотать как в несколько слоев, так и нированно, т. е., с обрывками Если используется толстый проводник, то элемент может обматываться без каркаса, если тонкий – то только на рамку. Эти каркасы катушек индуктивности бывают различного сечения: квадратные, круглые, прямоугольные. Полученная намотка может вставляться в специальный корпус какого-либо электрического устройства или использоваться в открытом виде.

Фото — конструкция самодельного элемента

Для увеличения индуктивности используются сердечники. В зависимости от назначения элемента, варьируется используемый материал стержня:

1. С ферромагнитным и воздушным сердечником применяются при высоких частотах тока;
2. Стальные используются в условиях низкого напряжения.

Вместе с этим, в электротехнике активно используются индуктивные классические катушки без сердечника, которые можно сделать своими руками при помощи намотки на немагнитный контур.Такие устройства имеют некоторые преимущества перед «сердечными». У них большая линейность импеданса. Но, у тороидальной модели намотка на немагнитный каркас способствует появлению паразитной емкости.

Исходя из принципа работы, бывают такие типы:

1. Контурные. Преимущественно используются в радиотехнике для создания колебательных контуров платы, работают вместе с конденсаторами. Для соединения используется последовательное подключение. Это современный вариант плоской контурной катушки Тесла;
2. Вариометры. Это высокочастотные перестраиваемые катушки, индуктивностью которыми можно при необходимости управлять при помощи дополнительных устройств. Они представляют собой соединение двух отдельных катушек, при этом, одна подвижна, а вторая нет;
3. Сдвоенные и подстроечные дроссели. Основные характеристики этих катушек: малое сопротивление постоянному току и высокое переменному. Дроссели изготавливаются из нескольких катушек, соединенных обмотками между собой. Их часто используют в виде фильтра для различных радиотехнических приборов, устанавливают для контроля помех в антенны и т. д.;
4. Трансформаторы связи. Их конструктивной особенностью является то, что на одном стержне установлено от двух и более катушек. Они используются в трансформаторах для обеспечения определенной связи между отдельными компонентами устройства.

Маркировка катушек индуктивности определяется по количеству витков и цвету корпуса.

Фото — маркировка

Форма

На рисунке слева – Ш-образный сердечник, справа – П-образный. A – толщина сердечника, B – высота окна сердечника, C – ширина окна сердечника, D – ширина зуба.

Делая прокладку в сердечнике, не забудьте, что ее толщина должна быть вдвое меньше расчетного зазора, так как магнитная линия в Ш и П – образных сердечниках пересекает ее дважды.

(читать дальше…) :: (в начало статьи)

:: ПоискТехника безопасности :: Помощь

К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.

Если что-то непонятно, обязательно спросите!Задать вопрос. Обсуждение статьи. сообщений.

Доброго дня. Можно ли применить методику для расчета моторного трехфазного дросселя (ПЧ+двигатель)? Какие особенности изготовления таких дросселей (например, взять три трансформатора и пр.)? Читать ответ…

Доброго здравия! По какой формуле включается предупреждение о недостаточности мощности сердечника? Читать ответ…

Здравствуйте! Я собираю сварочный инвертор по схеме из книги Негуляева (полумост резонансный), и пытался определить с помощью ваших онлайн-калькуляторов индуктивность дросселя резонанса, но в них надо подставлять известное значение индуктивности (и откуда, к слову, его взять если нет измерительных приборов) и получать витки. А мне то надо наоборот. Это нужно, чтобы попытать Читать ответ…

В расчёте дросселя, а именно определении зазора, есть расхождения около 30% в меньшую сторону. Как можете это прокомментировать. Читать ответ…

При токе 50-60 А на Ш образном сердечнике витки, расположенные в непосредственной близости к зазору начинают обугливаться. Любая железка, введённая в зазор просто плавится. Это же индукционка какая-то получается. Практика подсказывает, нужно как можно дальше удалять витки от зазора. Предпочтение в таких случаях отдаётся П – обр. сердечникам. Так ли это? Читать ответ…

Помимо непонятного выражения в формуле зазора, еще непонятно почему в других источниках приведены, кажется, какие-то иные расчеты? Вот например, в этой книге , я так понял, какой-то общий случай расчета, или почему-то другие они. Читать ответ…

Здравствуйте. А что значит выражение в формуле величины зазора в сердечнике? Читать ответ…

Спасибо за материал!
‘Провод 0.25мм’ – это диаметр или площадь сечения? Читать ответ…

Здравствуйте. Для сборки импульсного источника синусоидального напряжения расчитываю параметры дросселя L1. Имеющийся Ш-образный сердечник 20*28 N87 мал по размерам, как указывает онлайн расчет. Но в программе нет возможности по требуемым параметрам подобрать необходимый размер. Чтобы пойти и купить нужный. Подскажите или требуемые габаритные размеры или программку для выбора Читать ответ…

Здравствуйте, не могли бы вы помочь с расчётом дросселя для схемы опубликованной на вашем сайте: http://hw4.ru/circuitry-switching-sinus

В наличие имеется провод диаметром 0,5мм и ферритовые кольца B64290L0651X03
http://static.advonics.com/content/pdfs/221/7092193.pdf

Размер R22,1×13,7×12,5(mm)
Материал Т38
Начальная проницаемость 10 000

Номинальный вы Читать ответ…

Еще статьи

Изготовление дросселя, катушки индуктивности своими руками, самому, са…
Расчет и изготовление катушки индуктивности, дросселя. Типовые электронные схемы…

Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить…
Приемы намотки импульсного дросселя / трансформатора….

Импульсный источник питания. Своими руками. Самодельный. Сделать. Лабо…
Схема импульсного блока питания. Расчет на разные напряжения и токи….

Конструирование (проектирование и расчет) источников питания и преобра…
Разработка источников питания и преобразователей напряжения. Типовые схемы. Прим…

Проверка дросселя, катушки индуктивности, трансформатора, обмотки, эле…
Как проверить дроссель, обмотки трансформатора, катушки индуктивности, электрома…

Практика проектирования электронных схем. Самоучитель электроники….
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы….

Пушпульный импульсный источник питания. Онлайн расчет. Форма. Подавлен…
Как рассчитать пуш-пульный импульсный преобразователь напряжения. Как подавить п…

Повышающий импульсный источник питания. Онлайн расчет. Форма. Подавлен…
Как рассчитать повышающий импульсный преобразователь напряжения. Как подавить пу…

Варианты измерения

Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.

https://youtube.com/watch?v=BhnJnkggaXY

Прямой метод

Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.

Порядок проведения измерений включает в себя следующие этапы:

1. К прямопоказывающему приспособлению подключают катушку.
2. После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
3. Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.

Измерение выполняют путём проведения таких действий:

1. Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
2. Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
3. После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
4. Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
5. На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
6. После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
7. Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.

Косвенное определение

Для того чтобы измерить коэффициент самоиндукции, необходимо провести несколько подготовительных мероприятий. В первую очередь нужно собрать измерительную цепь по стандартной схеме, а также подготовить все необходимые приспособления (генератор синусоидального напряжения, частотомер, а также миллиамперметр и вольтметр, рассчитанные на переменный ток).

Порядок определения параметра:

1. К выходу генератора параллельно подключают вольтметр. Он должен быть переключён в режим, при котором верхнее предельное значение будет соответствовать напряжению в 3−5 вольт.
2. Аналогично подсоединяют и частотомер.
3. Отдельно собирают вторую цепь. В ней последовательно соединяют миллиамперметр и катушку, индуктивность которой нужно определить.
4. Затем обе цепи подключают параллельно друг к другу.
5. Подключённый генератор устанавливают в режим выработки синусоидального напряжения.
6. Путём изменения частоты добиваются такой работы приборов, при которой вольтметр будет показывать примерно 2 вольта. При этом сила тока на миллиамперметре будет постепенно уменьшаться.
7. После этого ручку частотомера перемещают в положение, соответствующее частоте измерений.
8. Как только эти действия будут выполнены, можно фиксировать значения.

Полученные данные переводятся в СИ, а затем выполняются все необходимые расчёты. Первым делом определяется индуктивное сопротивление. Для этого значения приборов подставляются в следующую зависимость: X=U/I, где U — напряжение, а I — сила тока. Результат расчётов будет выражен в омах.

После этого вычисляется индуктивность по формуле L=X/2 πF. В ней используются такие условные обозначения:

• X — индуктивное сопротивление;
• π — математическая постоянная (примерно 3,14);
• F — частота в герцах, при которой проводились измерения.

Индуктивность — это важный физический параметр, позволяющий определить магнитные свойства электроцепи. При точном его измерении и правильном проведении предусмотренных расчётов можно получить достоверные данные, которые понадобятся при выборе катушки.

https://youtube.com/watch?v=y4e5pNi9L5c

Похожие записи:

Светодиодные прожекторы на 50 вт: обзор моделей и цены Расчет освещенности помещения со светодиодными светильниками Обозначения постоянного и переменного тока: ac и dc ток Как выбрать узо + рейтинг лучших производителей Как защитить компьютер или ноутбук от плохой сети 220в. и надо ли защищать? Поезда на магнитной подушке