Электромагнитная индукция и магнитный поток ? спадило.ру

Магнитное поле

Уже в VI в. до н.э. в Китае было известно, что некоторые руды обладают способностью притягиваться друг к другу и притягивать железные предметы. Куски таких руд были найдены возле города Магнесии в Малой Азии, поэтому они получили название магнитов

Посредством чего взаимодействуют магнит и железные предметы? Вспомним, почему притягиваются наэлектризованные тела? Потому что около электрического заряда образуется своеобразная форма материи — электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют магнитным полем

Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами(северный и южный) . Разноименные магнитные полюса притягиваются, а одноименные — отталкиваются.

Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B

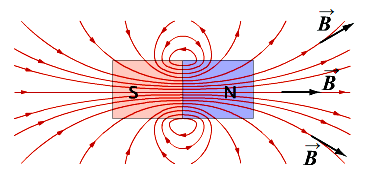
. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции ). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии — северный полюс (North), входят магнитные линии в южный полюс (South).

Магнитное поле можно сделать «видимым» с помощью железных опилок.

Теорема Гаусса для магнитного поля

Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:

∮B→dS→=.

Выражение ∮B→dS→= является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:

∮E→dS→=qε.

Запись ∮B→dS→= говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 1

Дан бесконечно длинный прямой проводник с током I, недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I’. Сторона рамки равна a. Она располагается в одной плоскости с проводом, как показано на рисунке 2. Значение расстояния от ближайшей стороны рамки до проводника равняется b. Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

Рисунок 2

Решение

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.

Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.

За основу возьмем формулу магнитного потока и работы, которая их связывает:

A=I’Φ2-Φ1 (1.1), где I’ принимают за силу тока в рамке, Φ1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b. Φ2=. Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы (1.1) изменится:

A=-I’Φ1 (1.2).

Перейдем к нормали n→ и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n→ и вектором B→ равняется π. Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:

dΦ=-BdS=-B·a·dx=-μ2πIldxx (1.3), значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:

B=μ2πxIl (1.4).

Отсюда следует, что для нахождения всего потока из (1.3) потребуется:

Φ1=∫S-μ2πIldxx=-μ2πIl∫bb+adxx=-μ2πIl·lnb+ab (1.5).

Произведем подстановку формулы (1.5) в (1.2). Искомая работа равняется:

A=I’μ2πIl·lnb+ab.

Ответ: A=μ2πII’l·lnb+ab.

Пример 2

Найти силу, действующую на рамку, из предыдущего примера.

Решение

Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние dx. Это говорит о совершении силой работы, равной:

δA=Fdx (2.1).

Элементарная работа δA может быть выражена как:

δA=I’dΦ (2.2).

Произведем то же с силой, применяя формулы (2.1), (2.2). Получаем:

Fdx=I’dΦ→F=I’dΦdx (2.3).

Используем выражение, которое было получено в примере 1:

dΦ=-μ2πIldxx→dΦdx=-μ2πIlx (2.4).

Произведем подстановку dΦdx в (2.3). Имеем:

F=I’μ2πIlx (2.5).

Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны AB и DC равные по модулю и противоположные по направлению. Выражение принимает вид:

FAB→+FDC→= (2.6), то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:

F→=FAD→+FBC→ (2.6).

Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:

F=FAD-FBC (2.7).

Произведем поиск силы FAD, действующей на сторону AD, применив формулу (2.5), где x=b:

FAD=I’м2πIlb (2.8).

Значение FBC будет:

FBC=I’μ2πIlb+a (2.9).

Для нахождения искомой силы:

F=I’μ2πIlb-I’μ2πIlb+a=II’μl2π1b-1b+a.

Ответ: F=II’μl2π1b-1b+a. Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Магнитное поле. Формулы ЕГЭ

3.3 МАГНИТНОЕ ПОЛЕ

3.3.1 Механическое взаимодействие магнитов

Около электрического заряда образуется своеобразная форма материи — электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют магнитным полем. Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами (северный и южный). Разноименные магнитные полюса притягиваются, а одноименные — отталкиваются.

Магнитное поле. Вектор магнитной индукции

Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии — северный полюс (North), входят магнитные линии в южный полюс (South).

Магнитная индукция B — векторная физическая величина, являющаяся силовой характеристикой магнитного поля.

Принцип суперпозиции магнитных полей — если магнитное поле в данной точке пространства создается несколькими источниками поля, то магнитная индукция — векторная сумма индукций каждого из полей в отдельности

Линии магнитного поля. Картина линий поля полосового и подковообразного постоянных магнитов

3.3.2 Опыт Эрстеда. Магнитное поле проводника с током. Картина линий поля длинного прямого проводника и замкнутого кольцевого проводника, катушки с током

Магнитное поле существует не только вокруг магнита, но и любого проводника с током. Опыт Эрстеда демонстрирует действие электрического тока на магнит. Если прямой проводник, по которому идёт ток, пропустить через отверстие в листе картона, на котором рассыпаны мелкие железные или стальные опилки, то они образуют концентрические окружности, центр которых располагается на оси проводника. Эти окружности представляют собой силовые линии магнитного поля проводника с током.

3.3.3 Сила Ампера, её направление и величина:

Сила Ампера — сила, действующая на проводник с током в магнитном поле. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера.

где I — сила тока в проводнике;

B — модуль вектора индукции магнитного поля;

L — длина проводника, находящегося в магнитном поле;

α — угол между вектором магнитного поля и направлением тока в проводнике.

3.3.4 Сила Лоренца, её направление и величина:

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца. Сила Лоренца определяется соотношением:

где q — величина движущегося заряда;

V — модуль его скорости;

B — модуль вектора индукции магнитного поля;

α — угол между вектором скорости заряда и вектором магнитной индукции.

Обратите внимание, что сила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно

Сила Лоренца перпендикулярна векторам В и v , и её направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного, например электрона), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца Fл.

Движение заряженной частицы в однородном магнитном поле

При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частица будет двигаться по окружности радиуса R:

R=mv/qB

Специальные правила

Рассмотрим варианты главного правила буравчика для частных случаев. Применение таких правил часто упрощает процесс вычислений.

Для векторного произведения

Расположите векторы так, чтобы их начальные точки совпадали. Для этой ситуации правило буравчика звучит так:

Если один из векторов сомножителей вращать кратчайшим способом до совпадения направлений со вторым вектором, то буравчик, вращающийся подобным образом, будет завинчиваться в сторону, куда указывает векторное произведение.

По циферблату часов

При расположении векторов способом совпадения их начальных точек можно определить направление вектора-произведения с помощью часовой стрелки. Для этого необходимо мысленно двигать кратчайшим путём один из векторов-сомножителей в сторону другого вектора. Тогда, если смотреть со стороны вращения этого вектора по часовой стрелке, то аксиальный вектор будет направлен вглубь циферблата.

Чему равно ЭДС индукции?

Для определения величины возникающей ЭДС рассмотрим контур помещенный в однородное магнитное поле с индукцией В, по данному контуру свободно может перемещаться проводник длиной l.

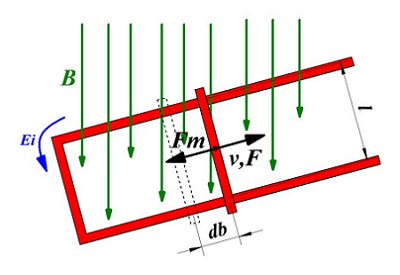
Под действием силы F проводник начинает двигаться со скоростью v. За некоторое время ∆t проводник пройдёт путь db. Таким образом, затрачиваемая работа на перемещение проводника составит

Так как проводник состоит из заряженных частиц – электронов и протонов, то они также движутся вместе с проводником. Как известно на движущуюся заряженную частицу действует сила Лоренца, которая перпендикулярна к направлению движения частицы и к вектору магнитной индукции В, то есть электроны начинают двигаться вдоль проводника приводя к возникновению электрического тока в нём.

Однако на проводник с током в магнитном поле действует некоторая сила Fт, которая в соответствии с правилом левой руки будет противоположна действию силы F, за счёт которой проводник движется. Так как проводник движется равномерно, то есть с постоянной скоростью, то силы Fт и F равны по абсолютному значению

где В – индукция магнитного поля,

I – сила тока в проводника, возникающая по действием ЭДС индукции,

l – длина проводника.

Так как путь db пройденный проводником зависит от скорости v и времени t, то работа, затрачиваемая на перемещения проводника, в магнитном поле составит

При перемещении проводника в магнитном поле практически вся затрачиваемая на эту работу механическая энергия переходит в электрическую энергию, то есть

Таким образом, преобразовав последнее выражение, получим значение ЭДС индукции при движении прямолинейного проводника в магнитном поле

где В – индукция магнитного поля,

l – длина проводника,

v – скорость перемещения проводника.

Данное выражение соответствует движению проводника перпендикулярно линиям магнитной индукции. Если происходит движение под некоторым углом к линиям магнитной индукции, то выражение приобретает вид

На практике достаточно трудно посчитать скорость перемещения проводника, поэтому преобразуем выражение к следующему виду

где dS – площадка, которую пересекает проводник при своём движении,

dΦ – магнитный поток пронизывающий площадку dS.

Таким образом, ЭДС индукции равна скорости изменения магнитного потока, который пронизывает контур.

Для обозначения направления движения тока в контуре вводят знак «–», который указывает, что ток в контуре направлен против положительного обхода контура. Таким образом

Зачастую в магнитном поле движется контур, состоящий из множества витков провода, поэтому ЭДС индукции будет иметь вид

где w – количество витков в контуре,

dΨ = wdΦ – элементарное потокосцепление.

Перефразируя предыдущее определение, ЭДС индукции в контуре равна скорости изменения потокосцепления этого контура.

Магнитное поле и его графическое изображение

На прошлых уроках мы выяснили, что причиной возникновения магнитной силы является наличие магнитного поля. Магнитное поле порождается движущимися электрическими зарядами и, в частности, электрическим током, поскольку это упорядоченный поток заряженных частиц. Например, магнитное поле образуется вокруг проводника с током. Каким же образом можно пояснить наличие магнитного поля у постоянных магнитов, у которых никаких видимых токов нет? Согласно гипотезе великого французского физика Ампера, в атомах и молекулах вещества в результате движения электронов возникают кольцевые токи. В магнитах такие кольцевые токи ориентируются одинаково. Магнитные поля, которые они образуют, направлены одинаково и усиливают друг друга. В результате образуется магнитное поле внутри и вблизи постоянного магнита. Когда мы ранее сталкивались с понятием «поле», то возникала проблема понимания, что же это такое. Если сравнивать с понятием «вещество», этой проблемы, очевидно, нет, так как из вещества созданы все окружающие нас тела, мы их можем потрогать, мы их можем увидеть. Что же касается магнитного поля, то это особый вид материи, который проявляется через взаимодействие с определенными телами. Вспомним, что гравитационное поле взаимодействует с телами, имеющими массу, то есть со всеми телами. При этом электрическое поле взаимодействует с телами, имеющими заряд, что же касается поля магнитного, то оно будет взаимодействовать с телами, в которых есть подвижные заряды. Из этого возникает вопрос: если поле нельзя увидеть, можно ли его как-то изобразить? Проведем эксперимент, возьмем обыкновенный полосовой магнит, положим его на стол и накроем обыкновенной прозрачной пластиковой накладкой. Сверху на поверхность накладки над магнитом аккуратно посыпаем железные опилки, в процессе посыпания мы можем увидеть интересный эффект: опилки будут распределяться неравномерным образом, образуя так называемые дорожки, и картина этих дорожек получается упорядоченной. Что же мы увидели и почему так происходит?

Рис. 4. Силовые линии магнитного поля в опыте железными опилками

Наш опыт позволяет наглядно продемонстрировать так называемые силовые линии магнитного поля (или, как их еще именуют, просто магнитные линии). Магнитные линии – это воображаемые линии, вдоль которых расположились бы маленькие магнитные стрелки, помещенные в магнитное поле. В нашем эксперименте в роли магнитных стрелок выступают железные опилки. Они имеют очень простое свойство намагничиваться во внешнем магнитном поле и выстраиваться вдоль магнитных линий, причем по правилу взаимодействия магнитов, то есть противоположными полюсами друг к другу. Стоит отметить, что магнитные линии могут быть как прямолинейными, так и криволинейными, при этом правило их построения очень простое: в любой точке нахождения магнитной стрелки касательная, проведенная через нее должна быть и касательной к магнитной линии.

Для того чтобы правильно изображать магнитное поле, не проводя постоянных экспериментов с железными опилками и магнитами, необходимо знать правило его построени.

Во-первых, силовые линии магнитного поля являются замкнутыми либо уходят на бесконечность. Кроме этого, следует помнить, что они выходят из северного полюса магнита и входят в южный. Во-вторых, наиболее сильное магнитное поле является у полюсов магнитов, что изображается как более плотное расположение магнитных линий, в областях же с менее сильным магнитным полем магнитные линии изображают на большем расстоянии друг от друга.

Какие же выводы мы можем сделать из этих правил?

Магнитные линии позволяют изображать направление поля в данной точке. Магнитные линии позволяют определять силу действия этого поля.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

(Здесь формулы приведем в СИ, в виде для вакуума, где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе наиболее важными являются:

Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:

B→(r→)=μ4π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}

B→(r→)=μ4π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
Теорема Ампера о циркуляции магнитного поля:

∮∂S⁡B→⋅dl→=μIS≡μ∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}

rotB→≡∇→×B→=μj→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:

Три из четырех уравнений Максвелла (основных уравнений электродинамики)

divE→=ρε, rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}

divB→=, rotB→=μj→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}

а именно:

Закон отсутствия монополя:

divB→=,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}

Закон электромагнитной индукции Фарадея:

rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}

Закон Ампера — Максвелла:

rotB→=μj→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}

Формула силы Лоренца:

F→=qE→+qv→×B→,{\displaystyle {\vec {F}}=q{\vec {E}}+q\left,}

Следствия из неё, такие как

Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

dF→=Idl→×B→,{\displaystyle d{\vec {F}}=\left,}

dF→=j→dV×B→,{\displaystyle d{\vec {F}}=\left,}

выражение для момента силы, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}

выражение для потенциальной энергии магнитного диполя в магнитном поле:

U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}

а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

Выражение для плотности энергии магнитного поля

w=B22μ{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}

Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Направление вектора

Наглядно продемонстрировать силовые линии магнитного поля можно, если на стеклянный лист, сквозь который пропущен проводник с током, равномерно (в один слой) разложить мелкие железные опилки. После включения тока опилки намагничиваются, то есть приобретают свойства магнитных стрелок и устанавливаются вдоль силовых линий поля . Таким образом результат действия магнитного поля на магнитные стрелки (железные опилки) или рамку с током можно применить для определения направления вектора магнитной индукции .

Рис. 2. Демонстрация силовых линий магнитного поля от прямого провода с током с помощью железных опилок.

Направлением вектора магнитной индукции принято считать направление от южного полюса S к северному полюсу N магнитной стрелки, которая ориентируется беспрепятственно и устанавливается в магнитном поле.

Это направление совпадает с направлением положительной нормали (перпендикуляра) к замкнутому контуру с током. Для определения этого направления применяется “правило буравчика”, которое звучит так: вектор направлен в ту сторону, куда перемещалась бы рукоятка буравчика (с правой резьбой) если ввинчивать его по направлению тока в рамке (или в проводе).

Визуальное (графическое) представление магнитного поля получается, если начертить так называемые линии магнитной индукции. Линия, в любой точке которой вектор магнитной индукции направлен по касательной, называется линией магнитной индукции или линией напряженности магнитной индукции. Картину линий магнитной индукции для постоянных магнитов, рамки с током и катушки можно сделать видимой, снова воспользовавшись мелкими железными опилками как в случае с прямолинейным проводом.

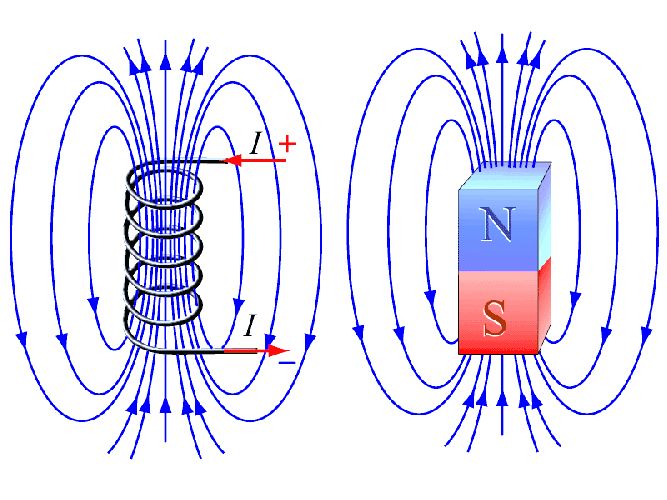
Рис. 3. Линии магнитной индукции катушки, рамки с током, постоянных магнитов.

Исследования показали, что линии напряженности магнитной индукции всегда замкнуты в отличие от линий напряженности электрического поля. Из этого фундаментального свойства следует, что в природе не существует магнитных зарядов, подобных электрическим. Магнитное поле возникает (индуцируется) от движущихся электрических зарядов или от переменного электрического поля.

Что мы узнали?

Итак, мы узнали, что является источником магнитного поля. Магнитная индукция — основная силовая характеристика этого поля. Визуальное (графическое) представление магнитного поля получается, если начертить так называемые линии магнитной индукции. Линия, в любой точке которой вектор магнитной индукции направлен по касательной, называется линией магнитной индукции или линией напряженности магнитной индукции.

Доска почёта

Чтобы попасть сюда – пройдите тест.

Дмитрий Карасев
5/5

Магнитное поле Земли

Земля является не только большим отрицательным зарядом и источником электрического поля, но в то же время магнитное поле нашей планеты подобно полю прямого магнита гигантских размеров.

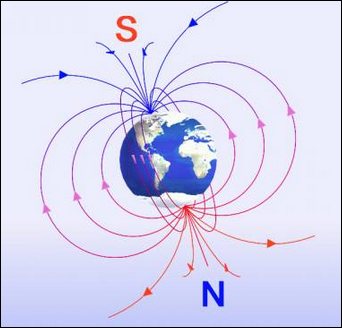
Географический юг находится недалеко от магнитного севера, а географический север приближен к магнитному югу. Если компас разместить в магнитном поле Земли, то его северная стрелка ориентируется вдоль линий магнитной индукции в направлении южного магнитного полюса, то есть укажет нам, где располагается географический север.

Характерные элементы земного магнетизма весьма медленно изменяются с течением времени — вековые изменения

. Однако время от времени происходят магнитные бури, когда в течение нескольких часов магнитное поле Земли сильно искажается, а затем постепенно возвращается к прежним значениям. Такое резкое изменение влияет на самочувствие людей.

Магнитное поле Земли является «щитом», прикрывающего нашу планету от частиц, проникающих из космоса («солнечного ветра»). Вблизи магнитных полюсов потоки частиц подходят гораздо ближе к поверхности Земли. При мощных солнечных вспышках магнитосфера деформируется, и эти частицы могут переходить в верхние слои атмосферы, где сталкиваются с молекулами газа, образуются полярные сияния.

Изображение линий магнитной индукции

Чтобы наглядно изучить распределение поля в пространстве, уменьшают размеры измерительных элементов. Для эксперимента подойдут железные опилки, равномерно рассыпанные на поверхности картонного листа или другой электрически нейтральной плоскости.

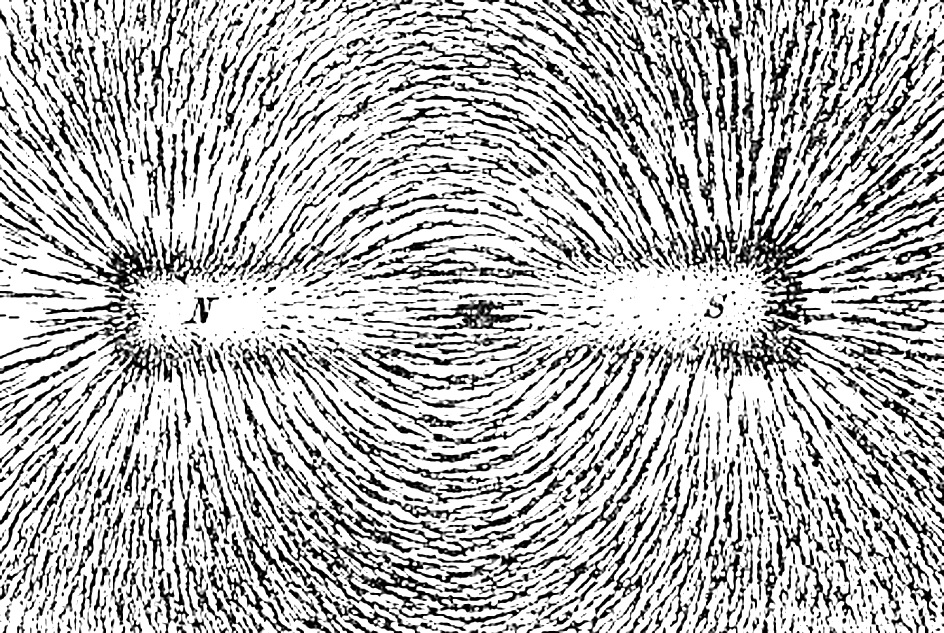Линии магнитной индукции – наглядное изображение распределения силового поля

Если поднести с обратной стороны магнит, металлические частицы, как миниатюрные стрелки компаса, распределяться вдоль силовых полос. По расстоянию между ними можно судить об энергетических параметрах поля в определенном месте. Аналогичным образом создают рисунок. Большая густота (около полюсов) свидетельствует об увеличенном значении индукции.

К сведению. Физическим разделением постоянного магнита на части не получится создать отдельные полюса. В этом – принципиальное отличие от электростатических зарядов определенной полярности, которые также создают силовое поле.

Представленные знания применяют для решения разных инженерных задач. В частности, пригодятся простые правила определения направления тока в проводнике и стороны, в которую перемещается сердечник соленоида.

Поезд на магнитной подушке разгоняется до высоких скоростей с минимальными энергетическими потерями

§ 84. Линии индукции магнитного поля. Единица индукции

Линия, проведенная в магнитном поле так, что в любой ее точке касательная совпадает с вектором индукции ( и рис. 119, а) магнитного поля в этой точке, называется линией индукции магнитного поля. Чтобы получить картину линий индукции, надо большое число магнитных стрелок поместить в магнитное поле. Расположение стрелок и покажет форму линий индукции. В качестве таких стрелок берутся железные опилки, которые в магнитном поле намагничиваются и, взаимодействуя друг с другом, сцепляются своими концами, образуя цепочки, изображающие линии индукции. За направление линии индукции принято направление, которое показывает северный полюс магнитной стрелки в данном месте поля. Поэтому вектор индукции в данной точке поля имеет направление, совпадающее с направлением линии индукции, проведенной через эту точку.

Рис. 119. Линии индукции магнитного поля

Линии индукции прямого проводника с током представляют концентрические окружности, расположенные в плоскостях, перпендикулярных направлению тока, причем центры всех этих окружностей находятся на оси проводника (см. рис.118, б). Их направление определяется по правилу буравчика. У магнитного поля прямого тока магнитных полюсов нет. Линии индукции, магнитного поля катушки с током внутри нее параллельны (см. рис. 119, б), а вне катушки не параллельны. Катушка с током имеет два магнитных полюса. Ее полярность, а следовательно, и направление линий индукции внутри катушки, определяется по правилу обхвата ее правой рукой (рис. 119, в): если взять катушку правой рукой так, чтобы четыре пальца указывали направление тока, то расположенный вдоль катушки большой палец укажет на конец катушки, который является северным магнитным полюсом, а также покажет направление линий индукции внутри катушки. Магнитные поля катушки с током и постоянного магнита тождественны. Северный и южный полюсы существуют только парами — получить один полюс невозможно.

Как и в случае электростатического поля, через каждую точку пространства можно провести только одну линию индукции. Следовательно, эти линии нигде не пересекают друг друга. В отличие от линий напряженности электростатического поля (см. рис. 50) линии индукции магнитного поля являются замкнутыми линиями как магнитного поля тока, так и постоянного магнита (рис. 119, г). Замкнутость линий индукции указывает на то, что магнитное поле является вихревым. Они всегда охватывают тот ток или движущийся заряд, с которым связано магнитное поле. Некоторые из линий индукции замыкаются в непосредственной близости тока, другие — вдали от него, и тогда нам кажется, что они уходят обоими концами в бесконечность (см. рис. 119, б, г).

Условились линии индукции проводить так, чтобы число линий, проходящих через единицу площадки, перпендикулярной вектору индукции в данной точке, было равно величине индукции поля в этом месте. Магнитные спектры дают представление о распределении магнитной индукции по величине и направлению.

Исходя из формулы индукции, установим единицу измерения индукции магнитного поля в Международной системе единиц:

Рис. 120. К понятию тесла и измерение магнитометром индукции магнитного поля магнита

За единицу индукции магнитного поля тесла принята индукция такого однородного магнитного поля, в котором на прямолинейный проводник длиной в 1 м, с током 1 а, расположенный перпендикулярно к линиям индукции*, действует сила в 1 н (рис. 120, а). На рис. 120, б показано измерение магнитометром величины магнитного поля постоянного магнита.

* ()

Индукция магнитного поля Земли невелика: у экватора около 32*10-6 тл, у полюсов — 65*10-6 тл, в районе Курской магнитной аномалии — 190*10-6 тл. В настоящее время в лабораториях с помощью катушек получены магнитные поля с индукцией до 15 тл.

Рис. 121. Зависимость индукции магнитного поля тока от формы проводника

Зависит ли величина индукции магнитного поля тока от формы проводника? Между сторонами проводника, имеющего форму, как на рис. 121, а, поместим магнитную стрелку и проводник подключим к источнику тока. Наблюдаем большое отклонение стрелки. Сделав проводник прямолинейным (рис. 121, б) и расположив под ним магнитную стрелку, пропустим по нему ток, как и в первом случае. Заметим небольшое отклонение стрелки. Скрутим проводник, как показано на рис. 121, в; видим, что стрелка не отклоняется, т. е. у скрученного (бифилярного) проводника магнитного поля нет. Чем больше индукция магнитного поля, тем сильнее оно действует на магнитную стрелку. Из опытов делаем вывод: величина индукции магнитного поля тока зависит от формы проводника: _а> _б, _в =0. При прочих равных условиях величина индукции магнитного поля наибольшая у проводника в форме катушки.

Электромагнитная индукция и магнитный поток