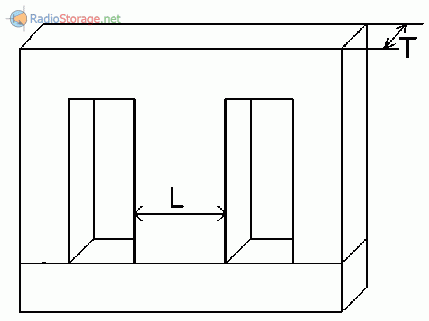
Конденсатор в цепи переменного или постоянного тока: как работает, сопротивление и напряжение

Работа конденсатора в электрической цепи

Уже давно мы отошли от понимания электричества в терминах движения, действия зарядов и так далее. Теперь мы мыслим понятиями электрических цепей, где обычными вещами являются напряжения, токи, мощность. И к рассмотрению поведения зарядов прибегаем только, чтобы понять, как работает в цепи какое-нибудь устройство.

Например, конденсатор в простейшей цепи постоянного электрического тока является просто разрывом. Обкладки ведь не соприкасаются друг с другом. Поэтому, чтобы понять принцип действия конденсатора в цепи, придется все-таки вернуться к поведению зарядов.

Зарядка конденсатора

Соберем простую электрическую цепь, состоящую из аккумулятора, конденсатора, резистора и переключателя.

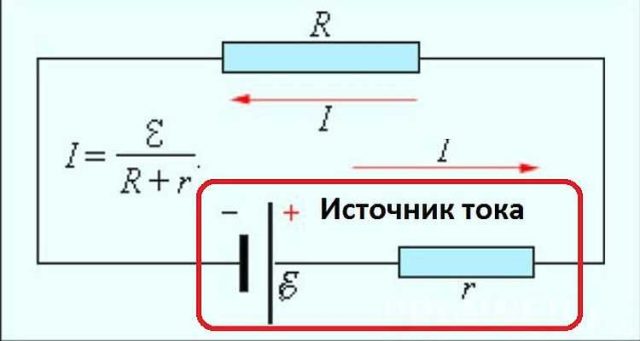
Конденсатор: принцип действия

ε_c – ЭДС аккумулятора, C – конденсатор, R – резистор, K – переключатель

Когда переключатель никуда не включен, тока в цепи нет. Если подключить его к контакту 1, то напряжение с аккумулятора попадет на конденсатор. Конденсатор начнет заряжаться настолько, насколько хватит его емкости. В цепи потечет ток заряда, который сначала будет довольно большим, а по мере зарядки конденсатора будет уменьшаться, пока совсем не сойдет на нуль.

Конденсатор при этом приобретет заряд такого же знака, как и сам аккумулятор. Разомкнув теперь переключатель К, получим разорванную цепь, но в ней стало два источник энергии: аккумулятор и конденсатор.

Конденсатор

Разрядка конденсатора

Если теперь перевести переключатель в положение 2, то заряд, накопленный на обкладках конденсатора, начнет разряжаться через сопротивление R.

Причем, сначала, при максимальном напряжении, и ток будет максимальным, величину которого можно вычислить, зная напряжение на конденсаторе, по закону Ома. Ток будет течь, то есть конденсатор будет разряжаться, а напряжение его падать. Соответственно и ток будет все меньше и меньше. И когда в конденсаторе заряда совсем не останется, ток прекратится.

Процессы внутри конденсатора

У ситуации, описанной в этих двух случаях, есть интересные особенности:

Электрическая батарея постоянного напряжения, работая в цепи с конденсатором, дает, тем не менее, переменный ток: при зарядке он изменяется от максимального значения до 0.
Конденсатор, имея некоторый заряд, при разряжении через резистор, даст тоже переменный ток, изменяющийся от максимального значения до 0.
В обоих случаях после непродолжительного действия ток прекращается. Конденсатор в обоих случаях после этого демонстрирует разрыв в цепи — ток больше не течет.

Описанные процессы называются переходными. Они имеют место в электрических цепях с постоянным напряжением питания, когда в них установлены реактивные элементы. После прохождения переходных процессов реактивные элементы перестают влиять на режимы токов и напряжений в электрической цепи. Время, в течение которого переходный процесс завершается, зависит как от емкости конденсатора C, так и от активного сопротивления нагрузки R. Очевидно, что чем они больше, тем больше нужен и интервал времени, пока переходный процесс не завершится.

Параметр, характеризующий время переходного процесса, называется «постоянной времени» для данной схемы, обозначается греческой буквой «тау»:

Формула

Произведение сопротивления в омах на емкость в фарадах, если рассмотреть внимательно эти единицы измерения, действительно дает величину в секундах.

Однако переходный процесс разрядки конденсатора — это процесс плавный. То есть, грубо говоря, он не заканчивается никогда.

Временная диаграмма разрядки конденсатора через резистор

U_c – напряжение на конденсаторе (вольт), U – первоначальное напряжение заряженного конденсатора, t – время (сек)

На рисунке видно, что конденсатор будет разряжаться «всегда», так как чем меньше на нем остается зарядов, тем меньший ток будет бежать по цепи, следовательно, тем медленнее будет идти процесс разрядки. Процесс экспоненциальный. По времени отложены значения в секундах величин, кратных постоянной времени. С некоторых значений можно считать процесс практически законченным, например, при 5t, когда напряжения на конденсаторе осталось порядка 0,7%.

Режим, когда переходный процесс завершен, называется стационарным, или режимом постоянного тока.

Основные величины и единицы измерения

Существует несколько основных величин, определяющих конденсатор. Одна из них — это его емкость (латинская буква С), а вторая – рабочее напряжение (латинская U). Электроемкость (или же просто емкость) в системе СИ измеряется в фарадах (Ф). Причем как единица емкости 1 фарад – это очень много – на практике почти не применяется. Например, электрический заряд планеты Земля составляет всего 710 микрофарад. Поэтому в большинстве случаев из-меряется в производных от фарада величинах: в пикофарадах (пФ) при очень маленьком значении емкости (1 пФ=1/10 6 мкФ), в микрофарадах (мкФ) при достаточно большом ее значении (1 мкФ = 1/10 6 Ф).

Для того чтобы рассчитать электроемкость, необходимо разделить величину заряда, накопленного между обкладками, на модуль разницы потенциалов между ними (напряжение на конденсаторе). Заряд конденсатора в данном случае – это заряд, накапливающийся на одной из обкладок рассматриваемого устройства. На 2-х проводниках устройства они одинаковы по модулю, но отличаются по знаку, поэтому сумма их всегда равняется нулю. Заряд конденсатора измеряется в кулонах (Кл), а обозначается буквой Q.

Назначение и функции конденсаторов

Конденсатор играет огромную роль как в аналоговой, так и цифровой технике. Они бывают электролитическими и керамическими, и отличаются своими свойствами, но не общей концепцией. Примеры использования:

Фильтрует высокочастотные помехи;
Уменьшает и сглаживает пульсации;
Разделяет сигнал на постоянные и переменные составляющие;
Накапливает энергию;
Может использоваться как источник опорного напряжения;
Создает резонанс с катушкой индуктивности для усиления сигнала.

Примеры использования

В усилителях обычно используются для защиты сабвуферов, фильтрации питания, термостабилизации и разделение постоянной составляющей от переменной. А электролитические в автономных схемах с микроконтроллерами могут долго обеспечивать питание за счет большой емкости.
В данной схеме транзистор VT1 постоянно открыт, чтобы усиливать звук без искажений. Но если вход замнется или на него поступи постоянный ток, то транзистор откроется, перейдет в насыщение и перегреется. Чтобы этого не допустить, нужен конденсатор. С1 позволяет отделить постоянную оставляющую от переменной. Переменный сигнал легко проходит на базу транзистора, а постоянный сигнал не проходит.

С2 совместно с резистором R3 выполняет функцию термостабилизации. Когда усилитель работает, транзистор нагревается. Это может внести искажения в сигнал. Поэтому, резистор R3 помогает удержать рабочую точку при нагреве. Но когда транзистор холодный и стабилизации не требуется резистор может уменьшить мощность усилителя. Поэтому, в дело вступает С2. Он проводит через себя усиленный сигнал шунтируя резистор, тем самым, не снижая номинальную мощность схемы. Если его емкость будет ниже расчетной, он начнет вносить фазовые искажения в выходной сигнал.

Чтобы схема качественно работала, обязательно хорошее питание. Когда схема в пиковые значения потребляет больше тока, то это всегда сильная нагрузка на источник питания. С3 фильтрует помехи по питанию и помогает снизить нагрузку. Чем больше емкость — тем лучше звук, но до определенных значений, все зависит от схемы.

А в блоках питания используется тот же принцип, как и в предыдущей схеме по питанию, но здесь емкость нужна гораздо больше. На этой схеме емкость элеткролита может быть как 1000 мкФ, так и 10 000 мкФ.

Еще на диодный мост можно параллельно включить керамические конденсаторы, которые будут шунтировать схему от высокочастотных наводок и шума сети 220 В.

Фазовые искажения

Конденсатор может искажать переменный сигнал по фазе. Это происходит из-за неверного расчета емкости, общего сопротивления и взаимодействия с другими радиодеталями. Не стоит забывать и о том, что любая радиодеталь имеет как реактивное, так и активное сопротивление.

Post Views:
1 363

Фазор

Благодаря фазовым векторам сложный и меняющийся во времени сигнал можно представить в виде комплексного числа (не зависит от времени) и сложного сигнала (зависит от времени). Фазоры делятся на основе А (амплитуды), v (частоты) и θ (фазы). Это приносит большую пользу, ведь частотный коэффициент часто выступает общим для всех компонентов линейной комбинации синусоид. В подобных ситуациях факторы исключают факультативную характеристику и основываются лишь на A и θ.

К примеру, можно представить A⋅cos (2πνt + θ) просто как комплексную постоянную Aeiθ. Из-за того, что фазовые векторы передаются величиной и углом, наглядно изображаются вектором в плоскости x-y.

Фазор можно рассматривать с позиции вектора, вращающегося вокруг начала координат. Косинусная функция – проекция вектора на ось. Амплитуда выступает модулем вектора. Постоянная фазы – угол, сформированный вектором и осью при t = 0

Соединение конденсаторов в батарею: способы выполнения

Существует 3 способа соединения, каждый из которых преследует свою определённую цель:

Параллельное – выполняется в случае необходимости увеличить ёмкость, оставив напряжение на прежнем уровне.
Последовательное – обратный эффект. Напряжение увеличивается, ёмкость уменьшается.
Смешанное – увеличивается как ёмкость, так и напряжение.

Теперь рассмотрим каждый из способов более подробно.

Параллельное соединение: схемы, правила

На самом деле всё довольно просто. При параллельном соединении расчёт общей ёмкости можно вычислить путём простейшего сложения всех конденсаторов. Итоговая формула будет выглядеть следующим образом: Собщ= С₁ + С₂ + С₃ + … + Сn. При этом напряжение на каждом их элементов будет оставаться неизменным: Vобщ= V₁ = V₂ = V₃ = … = Vn.

Получается, что подобный монтаж подразумевает подключение всех пластин конденсаторов к точкам питания. Такой способ встречается наиболее часто

Но может произойти ситуация, когда важно увеличить напряжение. Разберёмся, каким образом это сделать

Последовательное соединение: способ, используемый реже

При использовании способа последовательного подключения конденсаторов напряжение в цепи возрастает. Оно складывается из напряжения всех элементов и выглядит так: Vобщ= V₁ + V₂ + V₃ +…+ Vn. При этом ёмкость изменяется в обратной пропорции: 1/Собщ= 1/С₁ + 1/С₂ + 1/С₃ + … + 1/Сn. Рассмотрим изменения ёмкости и напряжения при последовательном включении на примере.

Дано: 3 конденсатора с напряжением 150 В и ёмкостью 300 мкф. Подключив их последовательно, получим:

напряжение: 150 + 150 + 150 = 450 В;
ёмкость: 1/300 + 1/300 + 1/300 = 1/С = 299 мкф.

Выполняют такое соединение в том случае, если есть опасность пробоя диэлектрика конденсатора при подаче напряжения в цепь. Но ведь существует и ещё один способ монтажа.

Полезно знать! Применяют также последовательное и параллельное соединение резисторов и конденсаторов. Это делается с целью снижения подаваемого на конденсатор напряжения и исключения его пробоя. Однако следует учитывать, что напряжения должно быть достаточно для работы самого прибора.

Смешанное соединение конденсаторов: схема, причины необходимости применения

Такое подключение (его ещё называют последовательно-параллельным) применяют в случае необходимости увеличения, как ёмкости, так и напряжения. Здесь вычисление общих параметров немного сложнее, но не настолько, чтобы нельзя было разобраться начинающему радиолюбителю.

Составим алгоритм вычислений.

всю схему нужно разбить на отдельные части, высчитать параметры которых просто;
высчитываем номиналы;
вычисляем общие показатели, как при последовательном включении.

Поведение конденсатора в цепи переменного тока

Если говорить строго, то через конденсатор не проходит ни постоянный, ни переменный ток, так как между обкладками находится изолятор, в котором свободные электрические заряды двигаться не могут.

Включение конденсатора в цепь постоянного тока равносильно разрыву этой цепи. Что же касается переменного тока, то он будет протекать по цепи, в которую включен конденсатор, благодаря периодическому заряду и разряду этого конденсатора. Действительно, когда происходит заряд конденсатора, то электрические заряды, например электроны, на одной обкладке накапливаются, а с другой обкладки уходят. При этом они, конечно, двигаются по соединительным проводам, подключенным к обкладкам конденсатора. Такое же движение зарядов, только в противоположном направлении, происходит и при разряде конденсатора.

Если включить конденсатор в цепь переменного тока, то он будет периодически заряжаться то в одной полярности, то в противоположной. Это значит, что электроны будут накапливаться то на одной, то на другой обкладке, и каждый раз при заряде и разряде свободные электроны будут двигаться по цепи, в которую включен конденсатор, не попадая, однако, в изолятор, включенный между обкладками. А поскольку под действием переменного напряжения в цепи конденсатора двигаются заряды, то мы считаем, что конденсатор пропускает переменный ток, хотя и в этом случае заряды не проходят через изолятор.

Конденсатор влияет на величину переменного тока в цепи, и поэтому (по аналогии с законом Ома) его часто рассматривают как сопротивление. Это так называемое емкостное сопротивление обозначается буквой х_с и так же, как и обычное сопротивление, измеряется в омах. Величина х_с зависит от частоты переменного тока и от емкости С конденсатора: с уменьшением емкости конденсатора, так же как и с уменьшением частоты переменного тока, емкостное сопротивление конденсатора увеличивается (рис. 80, 81, лист 87). Эту зависимость удобно записать в виде простой формулы:

Смысл этой формулы весьма прост: чем меньше емкость С, тем меньше зарядов будет двигаться к обкладкам при каждом заряде и разряде конденсатора; чем меньше частота переменного тока, тем реже будет заряжаться и разряжаться конденсатор. Отсюда следует, что с уменьшением f и С уменьшается ток в цепи, или, иными словами, растет сопротивление конденсатора.

Этот вывод имеет огромное практическое значение. Так, например, если нам понадобится включить в цепь конденсатор с очень маленьким емкостным сопротивлением, то емкость этого конденсатора нужно будет выбирать с учетом частоты переменного тока в цепи. Для высоких частот можно будет взять конденсатор небольшой емкости, а вот для низких частот емкость конденсатора придется взять большой. Это хорошо иллюстрируется простым примером. На частоте 100 кгц конденсатор емкостью 100 пф обладает емкостным сопротивлением х_с=16 ком. При уменьшении частоты в 1000 раз, то есть на частоте 100 гц, сопротивление конденсатора возрастет в 1000 раз и станет равным 16 000 ком (16 Мом). Для того чтобы при уменьшении частоты емкостное сопротивление не изменилось, нужно увеличить емкость конденсатора. Сопротивление 16 ком на частоте 100 гц будет иметь конденсатор емкостью 100 000 пф (0,1 мкф).

Из приведенной выше формулы следует также, что уменьшение емкости конденсатора связи С_св (лист 85) приведет к росту сопротивления этого конденсатора, а следовательно, к уменьшению тока в цепи антенны. Поэтому емкость С_св нельзя брать слишком малой.

Сказанное можно пояснить еще иначе. Конденсатор связи и колебательный контур Lк С_к можно рассматривать как делитель напряжения, к которому приложена э. д. с, действующая между зажимами А («антенна») и З («земля»). Мы не будем пока говорить о том, чему равно сопротивление колебательного контура — даже без этого ясно: чем больше емкостное сопротивление конденсатора связи, тем меньшая часть э. д. с. будет действовать на нижней части делителя — на контуре и подключенной к нему цепи детектор — телефон.

Читать дальше — Трансформаторная связь

Общая концепция

Конденсатор состоит из двух проводящих обкладок и диэлектрика между ними. И все, больше ничего. С виду простая радиодеталь, но работает на высоких и низких частотах по-разному.
Обозначается на схеме двумя параллельными линиями.

Принцип работы

Эта радиодеталь хорошо демонстрирует явление электростатической индукции. Разберем на примере.

Если подключить к конденсатору постоянный источник тока, то в начальный момент времени ток начнет скапливаться на обкладках конденсатора. Это происходит за счет электростатической индукции. Сопротивление практически равно нулю.

Электрическое поле за счет электростатической индукции притягивает разноименные заряды на две противоположные обкладки. Это свойство материи называется емкостью. Емкость есть у всех материалов. И даже у диэлектриков, но у проводников она значительно больше. Поэтому обкладки конденсатора выполнены из проводника.

Основное свойство конденсатора — это емкость. Она зависит от площади пластин, расстояния между ними и материала диэлектрика, которым заполняют пространство между обкладками.

По мере накопления зарядов, поле начинает ослабевать, а сопротивление нарастает. Почему так происходит? Места на обкладках все меньше, одноименные заряды на них действуют друг на друга, а напряжение на конденсаторе становится равным источнику тока. Такое сопротивление называется реактивным, или емкостным. Оно зависит от частоты тока, емкости радиодеталей и проводов.

Когда на обкладках не останется места для электрического тока, то и ток в цепи прекратится. Электростатическая индукция пропадает. Теперь остается электрическое поле, которое держит заряды на своих обкладках и не отпускает их. А электрическому току некуда деваться. Напряжение на конденсаторе станет равным ЭДС (напряжению) источнику тока.

А что будет, если повысить ЭДС (напряжение) источника тока? Электрическое поле начнет все сильнее давить на диэлектрик, поскольку места на обкладках уже нет. Но если напряжение на конденсаторе превысит допустимые знания, то диэлектрик пробьет. И конденсатор станет проводником, заряды освободятся, и ток пойдет по цепи. Как тогда использовать конденсатор для высоких напряжений? Можно увеличить размер диэлектрика и расстояние между обкладками, но при этом уменьшается емкость детали.

Между обкладками находится диэлектрик, который препятствует прохождению постоянного тока. Это именно барьер для постоянного тока. Потому, что постоянный ток создает и постоянное напряжение. А постоянное напряжение может создавать электростатическую индукцию только при замыкании цепи, то есть, когда конденсатор заряжается.

Так конденсатор может сохранять энергию до тех пор, пока к нему не подключится потребитель.

Конденсатор и цепь постоянного тока

Добавим в схему лампочку. Она загорится только во время зарядки.
Еще одна важная особенность — когда происходит процесс зарядки током, то напряжение отстает от тока. Напряжение как бы догоняет ток, поскольку сопротивление нарастает плавно, по мере зарядки. Электрические зарядам нужно время, чтобы переместиться к обкладкам конденсатора. Так называется время зарядки. Оно зависит от емкости, частоты и напряжения.

По мере зарядки, лампочка начинает тусклее светиться.

Лампочка затухает при полной зарядке.

Постоянный электрический ток не проходит через конденсатор только после его зарядки.

Цепь с переменным током

А что если поменять полярность на источнике тока? Тогда конденсатор начнет разряжаться, и снова заряжаться, поскольку меняется полярность источника.

Электростатическая индукция возникает постоянно, если электрический ток переменный. Каждый раз, когда ток начинает менять свое направление, начинается процесс зарядки и разрядки.

Поэтому, конденсатор пропускает переменный электрический ток.

Чем выше частота — тем меньше реактивное (емкостное) сопротивление конденсатора.

Как рассчитать импеданс в цепи

Импеданс – полное R тока, который обозначается Z. Этот параметр – отражение меняющегося во времени значения тока. Импеданс – векторная величина, которая состоит из двух значений: активное и реактивное сопротивление.

Активная часть импеданса, которая обозначается R – это мера степени, с которой материал будет противостоять движению электронов между атомными частицами. Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.

К материалам с минимальным сопротивлением можно отнести сталь, алюминий, золото. Самое большое значение R имеют стекло, слюда, полиэтилен и чаще всего их называют изоляторы или диэлектрики.

Если использовать резисторы в цепях синусоидального тока, то термин «импеданс» будет использоваться для обозначения сопротивления R=Z.

Практические расчеты импеданса чаще всего выполняются по следующей формуле:

Z = Um/Im.

Реактивное сопротивление обозначается X и является выражением степени, с которой электронный компонент схемы станет хранить или высвобождать электроэнергию, в то время, когда сила тока и значение напряжения станет колебаться при каждом цикле. Реактивное сопротивление выражается в числе Ом.

Энергия будет храниться и выделяться в двух типах:

Магнитного поля. Реактивная часть является индуктивной.
Электрического поля.

Где и зачем применяются конденсаторы

Где и почему используются эти приборы, которые могут работать в радиотехнических, электронных и электротехнических устройствах? Накопители используются в электротехнике при включении асинхронных моторов для сдвига фаз, без чего двигатель в составе однофазной цепи не будет функционировать. Если ёмкость составляет несколько фарад, то их применяют в электромобилях для питания мотора.

Применение возможно в разных сферах

Правильное использование этих приборов позволит получить лучший результат. Понимание основных принципов физики упрощает эксплуатацию оборудования. Неправильное применение чревато негативными последствиями, вызванными несоблюдением техники безопасности.

Источник

Особенности измерений

Если представить, что электрический ток — это текущая по трубе вода, а напряжение — действующий напор, то многие понятия и формулы становятся понятными. Когда труба перекрыта, то напор есть, а воды нет. Пока не появится потребитель, то есть нагрузка, он не потечет. А сопротивление — это подводные камни в русле, мешающие свободному прохождению потока, но заставляющие его работать.

Сила тока в физическом понимании — это количество заряженных частиц, протекающих в единицу времени через определенную точку системы. Измеряется она в амперах А или миллиамперах мА.

Измерения проводятся с помощью амперметров, а также бытовых или профессиональных мультиметров. Цифровые измерители просты и удобны в работе. Они позволяют установить не только силу тока и напряжение, но и другие характеристики — сопротивление, емкость конденсаторов, частоту переменного тока и т.д. Опасной для человека считается сила тока, превышающая 15 мА, при которой происходит спазм мышц. А удар в 100 мА — это практически всегда смертельный исход. Поэтому все работы, связанные с сетями под напряжением, должны производиться строго с соблюдением техники безопасности.

Как мультиметром измерить силу тока зарядного устройства

Устройство для зарядки аккумуляторов преобразует переменный ток из сети в постоянный с помощью трансформатора, выпрямителя и стабилизатора напряжения. Для автовладельцев производятся пуско-зарядные устройства — ПЗУ, — которые сочетают функции зарядки аккумулятора и запуска двигателя при севшей батарее. При этом заряда может вовсе не быть или в течение нескольких минут создается частичный заряд, необходимый для начала работы мотора.

В некоторых моделях ЗУ отсутствует индикация заряда, поэтому есть проблема с определением ампеража. Легко проверить силу тока можно обычным мультимером:

Аккумулятор необходимо снять с автомобиля и подключить к зарядке.
На мультиметре выставить шкалу на 10 А, а красный щуп вставить в разъем тоже на 10 А.
«Плюс» зарядного устройства присоединить к положительному полюсу батареи.
«Минус» зарядника соединить черным щупом с базой мультиметра (гнездо СОМ).
Красный щуп подключить ко второй клемме аккумулятора.

При включении зарядного устройства в сеть мультитестер покажет силу тока в цепи. Задача будет решена даже без амперметра-индикатора.