Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.
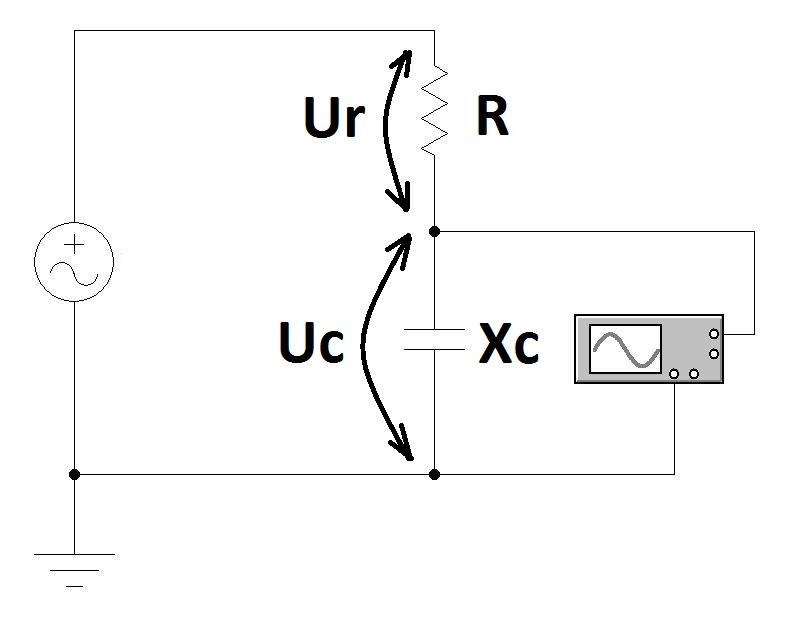 Косвенное измерение
Косвенное измерение
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд. Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше
Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Реализация кубика Рубика
Грани
Для представления кубика есть множество подходов, но я решил воспользоваться простым словарем, содержащим шесть матриц numpy 3×3 (по одной для каждой грани):
Для передней грани интуитивно ясно, что будет левым верхним углом. Однако значения , и зависят от того, с каком стороны вы смотрите на куб. Изображение ниже поможет избежать путаницы. Позиция обозначена фиолетовым. Схема согласована с тем, как определяется способ вращения.

Вращения
Numpy включает множество полезных методов, таких как и , которые отлично подходят для реализации вращения куба. В качестве примера проанализируем R:
Как видите, сначала мы выполняем вращение на матрице правой грани, а затем меняем значения нижней, передней, верхней и задней матриц соответственно.
Единственная сложность заключается в том, что при работе с обратной стороной необходимо инвертировать значения, как показано на изображении:

Полную реализацию можно посмотреть в исходном коде.
Обзор платы Arduino UNO R3 ATmega328P ATmega16U2.
Перед вами обе стороны Arduino UNO R3
Плата Arduino UNO R3 состоит из:
1. Микроконтроллер ATmega328P в качестве главного процессора.
2. Микроконтроллер ATmega16U2 для связи с компьютером через USB порт.
3. USB разъем для загрузки программ и подачи питания на плату.
4. Разъем для подключения от внешнего источника питания.
5. ICSP разъем для прошивки ATmega16U2.
6. ICSP разъем для прошивки ATmega328P.
7. Шина питания.
8. Шина аналоговых входов.
9. Две шины цифровых входов-выходов
10. Кнопка сброс (RESET)
11. Светодиод питания.
12. Светодиоды передачи данных по UART (RX, TX).
13. Светодиод подключенный к 13 контакту платы.
Практическое применение
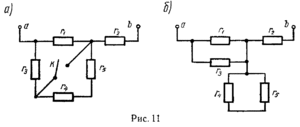
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
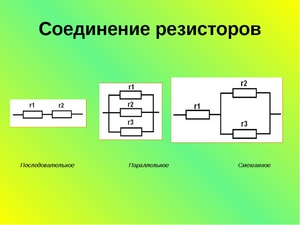
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
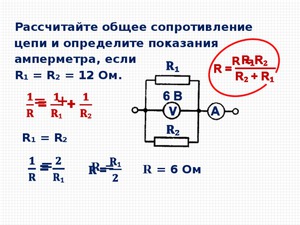
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
https://youtube.com/watch?v=HOdeO78Tzc4
Джоуль для измерения физических величин
Труды Джоуля позволили сформировать закон сохранения энергии. Отвечая на вопрос, что измеряется в джоулях, можно определить этой единицей количество работы, которая совершается в процессе перемещения точки приложения силы в количестве одного ньютона на расстояние в один метр в направлении действия приложенной силы. В теории электричества понятие джоуля эквивалентно работе, совершаемой силами электрического поля в течение 1 секунды с напряжением в 1 вольт, для того чтобы поддержать силу тока в 1 ампер.
Энергия по своей сути является физической величиной, отображающей переход материи из одного состояния в другое. Замкнутая физическая система позволяет сохранять энергию ровно столько времени, пока сама система находится в замкнутом состоянии. Это положение представляет собой закон сохранения энергии.
Энергия представлена различными видами. Кинетическая энергия связана со скоростью, которой обладают точки, движущиеся в механической системе. Для потенциальной энергии характерно создание определенных энергетических запасов, позволяющих в дальнейшем получить кинетическую энергию. Эти категории попадают под возможность их измерения в джоулях. Кроме того, существует энергия, связанная с внутренней энергией молекулярных связей. Широко известна ядерная и гравитационная энергия, а также энергия электрического поля.
В процессе механической работы один вид энергии превращается в другой. Данная физическая категория тесно связана с величиной и направлением силы, воздействующей на тело, а также с пространственным перемещением этого тела.
Важнейшим понятием классической термодинамики, измеряемым в джоулях, является теплота. В соответствии с ее первым началом, количество теплоты, получаемое системой, расходуется при совершении работы, которая требуется для противодействия внешним силам. Одновременно в процессе работы изменяется внутренняя энергия. Таким образом, для теплообмена, изменяющего внутреннюю энергию, обязательно совершение механической работы, измеряемой в джоулях.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
(a1+a2+…+an)2 = a12 + a22 + … + an-12 + an2 + 2 * a1 * a2 + 2 * a1 * a3 + 2 * a1 * a4 + … +
+ 2 * a1 * an-1 + 2 * a1 * an + 2 * a2 * a3 + 2 * a2 * a4 + … + 2 * a2 * an-1 + 2 * a2 * an +…+
+ 2 * an-1 * an
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
an − bn = (a − b) * (an-1 + an-2 * b + an-3 * b2 + … + a * bn-2 + bn-1).
Для четных показателей можно записать так:
a2*m − b2*m = (a2 − b2) *(a2*m−2 + a2*m−4 * b2 + a2*m−6 * b4 + … + b2*m−2).
Для нечетных показателей:
a2*m+1 − b2*·m+1 = (a − b) * (a2*m + a2*m−1 * b + a2*m−2 * b2 + … + b2*m).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Дополнительные методы расчета цепей
Закон Кирхгофа
Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:
- Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
- Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
- Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
- Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.
Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС. Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки
Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
«Механическая работа. Механическая мощность»
Код ОГЭ 1.16. Механическая работа. Формула для вычисления работы силы. Механическая мощность.
Работа силы – физическая величина, характеризующая результат действия силы.
Механическая работа А постоянной силы равна произведению модуля вектора силы на модуль вектора перемещения и на косинус угла а между вектором силы и вектором перемещения: А = Fs cos а.
Единица измерения работы в СИ – джоуль: = Дж = Н • м. Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы.
Анализ формулы для расчёта работы показывает, что механическая работа не совершается если:
- сила действует, а тело не перемещается;
- тело перемещается, а сила равна нулю;
- угол между векторами силы и перемещения равен 90° (cos a = 0).
Внимание! При движении тела по окружности под действием постоянной силы, направленной к центру окружности, работа равна нулю, так как в любой момент времени вектор силы перпендикулярен вектору мгновенной скорости. Работа – скалярная величина, она может быть как положительной, так и отрицательной. Работа – скалярная величина, она может быть как положительной, так и отрицательной
Работа – скалярная величина, она может быть как положительной, так и отрицательной.
- Если угол между векторами силы и перемещения 0° ≤ а < 90°, то работа положительна.
- Если угол между векторами силы и перемещения 90° < a ≤ 180°, то работа отрицательна.
Работа обладает свойством аддитивности: если на тело действует несколько сил, то полная работа (работа всех сил) равна алгебраической сумме работ, совершаемых отдельными силами, что соответствует работе равнодействующей силы.
Примеры расчёта работы отдельных сил:
Работа силы тяжести: не зависит от формы траектории и определяется только начальным и конечным положением тела: A = mg(h1 – h2)
По замкнутой траектории работа силы тяжести равна нулю.Внимание! При движении вниз работа силы тяжести положительна, при движении вверх работа силы тяжести отрицательна
Работа силы трения скольжения: всегда отрицательна и зависит от формы траектории. Если сила трения не изменяется по модулю, то её работа А = –Fтр l , где l – путь, пройденный телом (длина траектории). Очевидно, что чем больший путь проходит тело, тем большую по модулю работу совершает сила трения. Работа силы трения по замкнутой траектории не равна нулю!
Мощность N – физическая величина, характеризующая быстроту (скорость) совершения работы и равная отношению работы к промежутку времени, за который эта работа совершена: .
Мощность показывает, какая работа совершается за 1 с. Единица измерения мощности в СИ – ватт: = Дж/с = Вт. Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.
Может пригодиться! 1 л. с
(лошадиная сила) ~ 735 Вт.Внимание! Для случая равномерного движения (равнодействующая сила равна нулю) при расчете мощности отдельных сил, действующих на тело, получим
Для равноускоренного движения (F = const) где ʋср– средняя скорость движения за расчётный промежуток времени.
Конспект урока «Механическая работа. Механическая мощность».
Следующая тема: «Кинетическая и потенциальная энергия» (код ОГЭ 1.17)
Доходность Innosilicon T2-Turbo
Перейдем к самому интересному – доходности и окупаемости. По состоянию на 3 декабря 2020 года T2 Terminator (17.2 TH/s) и T2 Turbo (24 TH/s) майнят биткоин на сумму $10 и $25 в месяц соответственно.
Их сразу можно отбросить, поскольку окупаемость в этом случае составит 2.5-3 года.
T2 Turbo 25T и T2 Turbo+ 32T добывают криптовалюту на сумму $32 и $50 в месяц соответственно. Окупаемость T2 Turbo 25T находится на уровне 2.5 лет, а T2 Turbo+ 32T – порядка 3 лет.
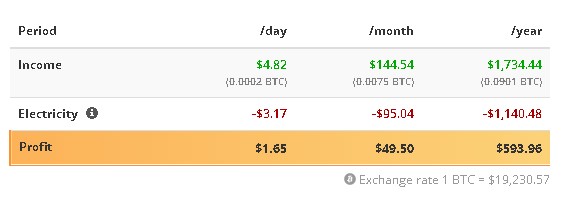
Доходность T2 Turbo+ 32T
В расчет бралась стоимость новых устройств, цена биткоина – $18 000 и текущий хешрейт сети.
Однако у нас есть Avito, поэтому можно рискнуть взять б/у устройство и сократить окупаемость до полугода. Например, T2 Turbo 25T можно приобрести примерно за $200 и окупаемость в этом случае составит ровно шесть месяцев.
8,720
Закон Джоуля – Ленца
Эмилий Христианович Ленц (1804 – 1865) – русский знаменитый физик. Он является одним из основоположников электромеханики. С его именем связано открытие закона, определяющего направление индукционного тока, и закона, определяющего электрическое поле в проводнике с током.
Кроме того, Эмилий Ленц и английский учёный-физик Джоуль, изучая на опыте тепловые действия тока, независимо один от другого открыли закон, согласно которому количество теплоты, которое выделяется в проводнике, будет прямо пропорционально квадрату электрического тока, который проходит по проводнику, его сопротивлению и времени, в течение которого электрический ток поддерживается неизменным в проводнике.
Данный закон получил название закон Джоуля – Ленца, формула его выражает следующим образом:
Q = kl²Rt, (1)
где Q – количество выделившейся теплоты, l – ток, R – сопротивление проводника, t – время; величина k называется тепловым эквивалентом работы. Численное значение этой величины зависит от выбора единиц, в которых производятся измерения остальных величин, входящих в формулу.
Если количество теплоты измерять в калориях, ток в амперах, сопротивление в Омах, а время в секундах, то k численно равно 0,24. Это значит, что ток в 1а выделяет в проводнике, который обладает сопротивлением в 1 Ом, за одну секунду число теплоты, которое равно 0,24 ккал. Исходя из этого, количество теплоты в калориях, выделяющееся в проводнике, может быть рассчитано по формуле:
Q = 0,24l²Rt.
В системе единиц СИ энергия, количество теплоты и работа измеряются единицами – джоулями. Поэтому коэффициент пропорциональности в законе Джоуля – Ленца равен единице. В этой системе формула Джоуля – Ленца имеет вид:
Q = l²Rt. (2)
Закон Джоуля – Ленца можно проверить на опыте. По проволочной спиральке, погружённой в жидкость, налитую в калориметр, пропускается некоторое время ток. Затем подсчитывается количество теплоты, выделившейся в калориметре. Сопротивление спиральки известно заранее, ток измеряется амперметром и время секундомером. Меняя ток в цепи и используя различные спиральки, можно проверить закон Джоуля – Ленца.
На основании закона Ома
I = U/R,
Подставляя значение тока в формулу (2), получим новое выражение формулы для закона Джоуля – Ленца:
Q = (U²/R)t.
Формулой Q = l²Rt удобно пользоваться при расчёте количества теплоты, выделяемого при последовательном соединении, потому что в этом случае электрический ток во всех проводниках одинаков. Поэтому, когда происходит последовательное соединение нескольких проводников, в каждом из них будет выделено такое количество теплоты, которое пропорционально сопротивлению проводника. Если соединить, например, последовательно три проволочки одинаковых размеров – медную, железную и никелиновую, то наибольшее количество теплоты будет выделяться из никелиновой, так как удельное сопротивление её наибольшее, она сильнее и нагревается.
Если проводники соединить параллельно, то электрический ток в них будет различен, а напряжение на концах таких проводников одно и то же. Расчёт количества теплоты, которое будет выделяться при таком соединении, лучше вести, используя формулу Q = (U²/R)t.
Эта формула показывает, что при параллельном соединении каждый проводник выделит такое количество теплоты, которое будет обратно пропорционально его проводимости.
Если соединить три одинаковой толщины проволоки – медную, железную и никелиновую – параллельно между собой и пропустить через них ток, то наибольшее количество теплоты выделится в медной проволоке, она и нагреется сильнее остальных.
Беря за основу закон Джоуля – Ленца, производят расчёт различных электроосветительных установок, отопительных и нагревательных электроприборов. Также широко используется преобразование энергии электричества в тепловую.
fb.ru
Джоуль.
Джоуль – единица измерения работы, энергии и количества теплоты в Международной системе единиц (СИ). Имеет русское обозначение – Дж и международное обозначение – J.
Другие единицы измерения
Джоуль, как единица измерения:
Джоуль – единица измерения работы, энергии и количества теплоты в Международной системе единиц (СИ), названная в честь английского физика Джеймса Прескотта Джоуля.
Джоуль как единица измерения имеет русское обозначение – Дж и международное обозначение – J.
В классической физике джоуль равен работе, совершаемой при перемещении точки приложения силы, равной 1 (одному) ньютону (Н), на расстояние одного метра в направлении действия силы.
Дж = Н · м = кг · м2 / с2.
1 Дж = 1 Н · 1 м = 1 кг · 1 м2 / 1 с2.
В электричестве джоуль означает работу, которую совершают силы электрического поля за 1 секунду при напряжении в 1 вольт (В) для поддержания силы тока в 1 ампер (А). Это энергия, которая выделится за 1 секунду при прохождении тока через проводник силой тока 1 ампер (А) при напряжении 1 вольт (В).
В Международную систему единиц джоуль введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы джоуль пишется со строчной буквы, а её обозначение – с заглавной (Дж). Такое написание обозначения сохраняется и в обозначениях других производных единиц, образованных с использованием джоуля.
Представление джоуля в других единицах измерения – формулы:
Через основные единицы системы СИ джоуль выражается следующим образом:
Дж = Н · м
Дж = кг · м2 / с2.
Дж = Вт / с.
Дж = А2 · Ом · с.
Дж = В2 · с / Ом.
Дж = Кл · В.
где А – ампер, В – вольт, Дж – джоуль, Кл – кулон, м – метр, Н – ньютон, с – секунда, Вт – ватт, кг – килограмм, Ом – ом.
Перевод в другие единицы измерения:
1 Дж ≈ 6,24151 ⋅ 1018 эВ
1 МДж = 0,277(7) кВт · ч
1 кВт · ч = 3,6 МДж
1 Дж ≈ 0,238846 калориям
1 калория (международная) = 4,1868 Дж
1 килограмм-сила-метр (кгс·м) = 9,80665 Дж
1 Дж ≈ 0,101972 кгс·м
Кратные и дольные единицы:
Кратные и дольные единицы образуются с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Дж | декаджоуль | даДж | daJ | 10−1 Дж | дециджоуль | дДж | dJ |
| 102 Дж | гектоджоуль | гДж | hJ | 10−2 Дж | сантиджоуль | сДж | cJ |
| 103 Дж | килоджоуль | кДж | kJ | 10−3 Дж | миллиджоуль | мДж | mJ |
| 106 Дж | мегаджоуль | МДж | MJ | 10−6 Дж | микроджоуль | мкДж | µJ |
| 109 Дж | гигаджоуль | ГДж | GJ | 10−9 Дж | наноджоуль | нДж | nJ |
| 1012 Дж | тераджоуль | ТДж | TJ | 10−12 Дж | пикоджоуль | пДж | pJ |
| 1015 Дж | петаджоуль | ПДж | PJ | 10−15 Дж | фемтоджоуль | фДж | fJ |
| 1018 Дж | эксаджоуль | ЭДж | EJ | 10−18 Дж | аттоджоуль | аДж | aJ |
| 1021 Дж | зеттаджоуль | ЗДж | ZJ | 10−21 Дж | зептоджоуль | зДж | zJ |
| 1024 Дж | иоттаджоуль | ИДж | YJ | 10−24 Дж | иоктоджоуль | иДж | yJ |
Интересные примеры:
Дульная энергия пули при выстреле из автомата Калашникова – 2030 Дж.
Энергия, необходимая для нагрева 1 литра воды от 20 до 100 °C, составляет 3,35⋅105 Дж.
Энергия, выделяемая при взрыве 1 тонны тринитротолуола (тротиловый эквивалент), – 4,184⋅109 Дж.
Примечание: Фото https://www.pexels.com, https://pixabay.com
Найти что-нибудь еще?
карта сайта
формула энергии закон джоуля ленца можно тепловой 1 м дж джоуль ленц закон равен 2 2 равен единица теплота масса тела сила количество теплоты работа кинетическая энергия в джоулях в секунду 10 5 8 6 20 200 100 виды сколько степени джоулейкилоджоули скорость в джоули в кг килограммы 3 4 джоуля
Коэффициент востребованности
5 394
Что делать, если скоро появится DVB-T3
Стандарт DVB-T просуществовал лет десять. Приход формата второго поколения заставил потребителя менять приемные устройства на новые. Возникает вопрос, не ожидает ли DVB-T2 участь предшественника.
В ближайшие десятилетия этого не произойдет. В обозримом будущем достичь увеличения скорости передачи данных невозможно, а дальнейшее сжатие только приведет к дефектам картинки. Так что телезрители могут выдохнуть и рассчитывать на долгосрочное использование современного оборудования.
Предыдущая
ТехнологияЧастоты эфирных цифровых каналов DVB-T2 для ручной настройки
Следующая
ТехнологияCтандарты цифрового телевидения: DVB-T, DVB-T2, DVB-C, DVB-C2, DVB-S, DVB-S2
Хорошее ли это решение?
«Команда исследователей (при поддержке Google) решила каждую позицию кубика Рубика и установила, что каждая из них занимает не более двадцати ходов».
В предыдущем запуске решение состояло из 276 ходов, что далеко от оптимального. Однако имейте в виду, что в данном случае перестановки вносили постепенные изменения в очень маленькие части куба в качестве требования для работы ГА, поэтому это не очень справедливое сравнение. Для нашего подхода более близки методы, используемые для решения вслепую, а такие решения нередко находятся в диапазоне сотен ходов. Поэтому наше решение, возможно, не такое уж и плохое. ?
Итак, какие же недостатки у ГА:
- Трудность нахождения лучшего решения. Обычно генетический алгоритм находит «достаточно хорошее» и продолжает работать над ним.
- Настройка параметров может потребовать много времени и экспериментов.
- Результаты недетерминированы. Вы получите разные решения, и время на их поиск во многих случаях может существенно различаться.
Заключение
Это был интересный проект, а результаты получились вполне удовлетворительными. Если вы хотите поэкспериментировать или улучшить программу, то ловите исходный код на GitHub.
Благодарим за чтение!
- Безградиентный подход к оптимизации нейронной сети
- Поиск с возвратом в решении типичных задач на собеседовании
- От Spotify к собственной рекомендательной системе
Читайте нас в Telegram, VK и
Перевод статьи Roberto Vaccari: Solving Rubik’s cube using Genetic Algorithms




