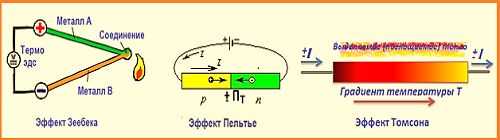
Эффект Зеебека и Пельтье
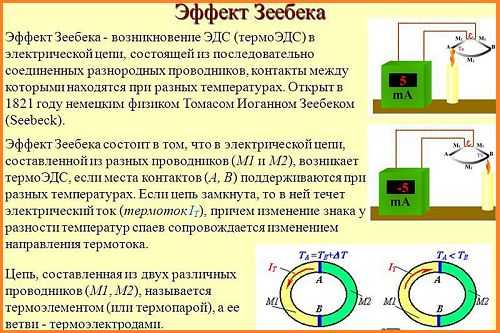
Суть эффекта Зеебека заключается в образовании электродвижущей силы в электрическом контуре, в состав которого входят проводники А и В, контакты которых обладают разными температурами Т1 и Т2. Данные свойства позволяют выполнять прямое преобразование тепловой энергии в электрическую.
В результате широкое применение в различных областях получил эффект Зеебека, формула которого определяет термо-ЭДС контура: где значения SA и SB являются абсолютными термоэлектродвижущими силами проводников А и В. Абсолютная термо-ЭДС относится к одной из характеристик проводника и представляет собой S=du/dT, где u является электродвижущей силой, возникающей в проводнике при наличии в нем разницы температур. Таким образом, теоретические основы эффекта Зеебека тесным образом связаны с температурными перепадами.
Элемент Пельтье является полной противоположностью устройствам, созданным на основе эффекта Зеебека. В данном случае, наоборот, под действием электрического тока образуется разница температур на рабочих площадках конструкции. Таким образом, с помощью электрического тока осуществляется перенос тепла с одной термопары на другую. При изменении направления тока нагреваемая сторона будет принимать противоположное состояние.
Данный эффект происходит в двух разнородных проводниках с одинаковой проводимостью. В каждом из них электроны обладают разным значением энергии и расположены они на очень близком расстоянии между собой. В результате произойдет перенос зарядов из одной среды в другую, и электроны с более высокой энергией на фоне низких уровней, отдадут излишки кристаллической решетке, вызывая нагрев. При недостатке энергии она, наоборот, передается от кристаллической решетки, приводя к охлаждению спая.
В случае неодинакового типа проводимости, полупроводников присутствующих в термопаре, эффект Пельтье будет выглядеть несколько иначе. При попадании в р-материал, электрон занимает место дырки на энергетическом уровне. В результате, у него теряется кинетическая энергия движения и наступает изменение состояния. Высвобожденная энергия способствует образованию свободных носителей с обеих сторон р-п-перехода, а оставшаяся часть уходит на кристаллическую решетку, которая и вызывает нагрев. Если в начальный момент значение энергии меньше, то спай начнет охлаждаться.
https://youtube.com/watch?v=r97NRWNZVbs
Открытие Томаса Иоганна Зеебека
В 1821 году эстонско-немецкий физик Томас Зеебек провел один любопытный эксперимент: он соединил между собой две пластины, которые были изготовлены из разных материалов (висмут и медь) в замкнутый контур. Затем он нагрел один из контактов. Ученый наблюдал, что магнитная стрелка компаса, который находился поблизости от проводящего контура, начала изменять свое направление. В итоге ученый решил, что два материала (медь и висмут) поляризуются по-разному в результате действия тепла, поэтому определил открытый эффект как термомагнитный, а не термоэлектрический.
Впоследствии уже датский ученый Ханс Эрстед дал правильное объяснение открытому Зеебеком эффекту, назвав его термоэлектрическим процессом.
Свойства материалов
Напомним себе, что трибоэлектрическая плотность заряда напрямую зависит от нескольких факторов: трибоэлектрического ряда (чем дальше друг от друга вещества, тем лучше они взаимодействуют, в ролике выше это упоминается), структурирования трибоэлектрических поверхностей, площади контакта под воздействием прилагаемой силы и от факторов окружающей среды.
Для проверки того что и как на что влияет была использована DDEF модель при синусоидальном движении (частота = 1 Гц, амплитуда = 1 мм), при этом параметры устройства совпадают с теми, что в практическом эксперименте.
Анализ данных показывает, что показатель выходной мощности возрастает при увеличении плотности заряда. При этом внутренний импеданс не меняется при изменении плотности заряда.
А вот изменения параметров в окружающей среде, таких как влажность, температура и давление, естественно, влияют на плотность заряда, делая этот показатель нестабильным. Если же устройство работает в контролируемой среде, то удается сохранить стабильность этого показателя. Конечно, это весьма печально, так как на практике мы не будем пользоваться своими устройствами только в определенных условиях. Посему этот момент также отправлен учеными на дальнейшую доработку и исследование.
Также ученые отмечают, что данный теоретический эксперимент хоть и показывает яркие взаимосвязи, но на практике крайне сложен в реализации, поскольку изменение какого-то параметра материала в реальности означает замену самого материала, а это значит и изменение всех других свойств.
Термопара
Термоэлектричество используют для генерации электрического тока. Отдельная термопара (термоэлемент) наделен очень небольшой электродвижущей силой. Для получения значительных напряжений термоэлементы соединяют последовательно в батареи. Все нечетные спаи поддерживают на одной температуре, а все четные – при другой температуре. Причем электродвижущие силы отдельных элементов можно складывать. Термобатарея наподобие тепловой машины, включенной между нагревателем и холодильником. В этой машине большее количество теплоты, полученного от нагревателя, растрачивается на джоулево тепло и теплопроводность. Термобатареи из металлических термопар характеризуются слишком маленьким КПД (приблизительно ,1%). Металлические термопары применяют лишь для установления температур и потоков лучистой энергии. Намного продуктивнее работают батареи термопар из полупроводников. Причем 1 ветвь термопары делают из полупроводника с электронной проводимостью, а 2-ю – из полупроводника с дырочной проводимостью. Коэффициент полезного действия полупроводниковых термопар доходит до 15%.
Пример 2
Необходимо найти термо ЭДС пары железо–константан. При условии что абсолютные значения α по отношению к платине находятся в интервале температур –100°С для Железа α1-αPt=+16 мкВК, для константана α2-αPt=-34,4 мкВК.
Решение
Дифференциальная термо ЭДС данной цепи равняется:
16-(-34,4)=50,4 мкВК.
При условии разности температур спаев:
T2-T1=100 К.
Тогда термо ЭДС данной пары будет равняться:
50,4·100=5,04 (мВ).
Ток в горячем спае будет протекать в направлении от константана к железу.
Ответ: 5,04 мВ
Пример 3
Необходимо объяснить, почему появляется термо ЭДС.
Решение
Для понимания причины появления термо ЭДС применим цепь из 2-х проводников (рисунок 1). Пускай температура контакта B равна T1, температура контакта С равна T(Ti>T)Температура контактов А и D одинаковая и равняется T. Тепловые скорости электронов возле контакта B больше по сравнению с теми, что возле контакта С. Поэтому во 2-м проводнике появится поток диффундирующих электронов, направленный по направлению от B к С. На поверхности 2-го проводника образуются электрические заряды, а это означает, что возникает электрическое поле, его значение таково, что в установившемся состоянии данное поле порождает такой ток дрейфа, который может компенсировать ток диффузии.
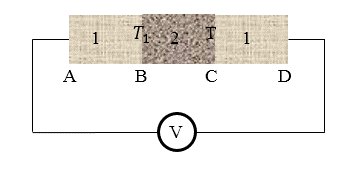
Рисунок 1
Следовательно, если в проводнике существует градиент температур, тогда в нем возникает градиент электрического потенциала.
Помимо этого, термо ЭДС вызывается не только диффузией в объеме, но также и контактными скачками потенциала φi12 и φi21. Поскольку они зависят от температуры, тогда их сумма не равна . Напряжение, регистрируемое вольтметром на рисунке 1, равное термо ЭДС, суммируется из падения напряжения в объеме проводников и скачков потенциала в контактах.
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Предпосылки открытия эффекта
В 1797 году итальянский физик Алессандро Вольта, проводя исследования в области электричества, открыл одно из удивительных явлений: он обнаружил, что при контакте двух твердых материалов в области контакта появляется разность потенциалов. Она получила название контактной разности. Физически этот факт означает, что зона соприкосновения разнородных материалов обладает электродвижущей силой (ЭДС), способной привести к появлению тока в замкнутой цепи. Если теперь соединить в одну цепь два материала (сформировать два контакта между ними), то на каждом из них появится указанная ЭДС, которая будет одинакова по модулю, но противоположна по знаку. Последнее объясняет, почему не возникает никакого тока.
Вам будет интересно:Ударение в слове «звонит»: есть ли ошибка популярнее?
Вам будет интересно:Шарада — это многозначное слово
Канал ДНЕВНИК ПРОГРАММИСТА
Жизнь программиста и интересные обзоры всего. Подпишись, чтобы не пропустить новые видео.
https://youtube.com/watch?v=fQO8S63TtQc
Причиной появления ЭДС является разный уровень Ферми (энергии валентных состояний электронов) в разных материалах. При соприкосновении последних уровень Ферми выравнивается (в одном материале понижается, в другом — повышается). Этот процесс происходит за счет перехода электронов через контакт, что и приводит к появлению ЭДС.
Сразу следует отметить, что величина ЭДС является незначительной (порядка нескольких десятых вольта).
Частота
График выше (а) это сравнение пиковых показателей мощности теоретической модели DDEF (зависимое от расстояния электрическое поле) и теории TENG-слоев при разной частоте (от 0.1 Гц до 1000 Гц). В свою очередь график (b) показывает сравнение данных модели DDEF, теории TENG-слоев плюс экспериментальных данных, полученных опытным путем при частоте от 0.1 Гц до 10 Гц.
Получается, что способы, простые и эффективные, для увеличения частоты, а следовательно и выходной мощности, есть. Однако стоит отметить, что частота также не может быть больше определенного уровня (10 ГГц), что связано с диэлектрическими потерями, возникающими при больших частотах.
Термоэлектрические устройства и применение эффекта Зеебека
Термоэлектрическими материалами чаще всего являются сплавы, свойства которых похожи на полупроводниковые. К этой же категории можно отнести и некоторые химические соединения со специфическими параметрами, делающими их пригодными для использования в термоэлектрических устройствах.
Существуют три основных варианта применения эффекта Зеебека в различных конструкциях и устройствах:
- Термоэлектрические генераторы.
- Термоэлектрические холодильники.
- Измерители температур в широком диапазоне: от абсолютного нуля до нескольких тысяч градусов по Кельвину.
Незначительная разница температур между спаями, как показали опыты, приводит к появлению термоэлектродвижущей силы, которая пропорциональна температурной разнице элементов, включенных в цепь. Однородные проводники, работающие по закону Ома, имеются в любой диаде. В свою очередь, в ней возникает термоэлектродвижущая сила, которая определяется свойствами проводников и разницей температур. При этом, распределение температуры между контактами не играет какой-либо решающей роли. Это и есть термоэлектрический эффект Зеебека.
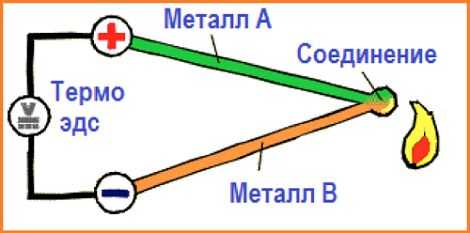
Если цепь состоит всего лишь из двух разных проводников, то данная комбинация будет называться термопарой. Уровень термо-ЭДС в этом случае зависит от материалов проводников и разницы температур между контактами. В большинстве случаев термопара применяется для определения температурных значений. Измерения до 1400 градусов по Кельвину может производится измерителями, в состав которых входят неблагородные элементы. При температуре 1900 градусов и выше потребуются металлы платиновой группы. Для специальных измерителей очень высоких температур применяются особые жаростойкие сплавы.
Преобразование тепловой энергии в электрическую осуществляется с помощью термоэлектрических генераторов. Основной рабочий процесс этих устройств также связан с эффектом Зеебека. За счет этого может преобразовываться даже сбросовая тепловая энергия, выделяемая двигателями машин. Полученная таким путем электроэнергия используется по своему назначению для питания различных устройств.
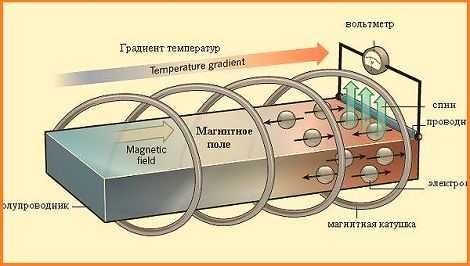
Преимуществами таких генераторов является продолжительный срок эксплуатации и возможность их хранения в нерабочем состоянии без каких-либо ограничений. Они отличаются надежностью и устойчивым режимом работы, полностью устраняют риск коротких замыканий. Работа этих устройств абсолютно бесшумна, так как в их конструкции не содержатся подвижные элементы.
Широкого применения эти устройства не получили только по причине низкого коэффициента эффективности, составляющего 3-8%. Однако при отсутствии обычных ЛЭП и низкой предполагаемой нагрузке, использование таких генераторов будет вполне оправданным. В результате, эффект Зеебека применение нашел в области энергообеспечения космической техники, в преобразователях солнечной энергии, отопительных системах и многих других областях, где использование традиционных источников электроэнергии не представляется возможным.
Коэффициенты Зеебека для некоторых распространенных материалов
В таблице ниже приведены коэффициенты Зеебека при комнатной температуре для некоторых распространенных, неэкзотических материалов, измеренные относительно платины. Коэффициент Зеебека самой платины составляет приблизительно -5 мкВ / К при комнатной температуре, поэтому значения, перечисленные ниже, должны быть соответственно скомпенсированы. Например, коэффициенты Зеебека для Cu, Ag, Au составляют 1,5 мкВ / К, а для Al -1,5 мкВ / К. Коэффициент Зеебека полупроводников очень сильно зависит от легирования, с обычно положительными значениями для материалов с p-легированием и отрицательными значениями для n-легирования.
| Материал | Коэффициент Зеебека относительно платины (мкВ / К) |
|---|---|
| Селен | 900 |
| Теллур | 500 |
| Кремний | 440 |
| Германий | 330 |
| Сурьма | 47 |
| Нихром | 25 |
| Молибден | 10 |
| Кадмий , вольфрам | 7,5 |
| Золото , серебро , медь | 6.5 |
| Родий | 6.0 |
| Тантал | 4.5 |
| Вести | 4.0 |
| Алюминий | 3.5 |
| Углерод | 3.0 |
| Меркурий | 0,6 |
| Платина | 0 (определение) |
| Натрий | -2,0 |
| Калий | -9,0 |
| Никель | -15 |
| Константин | -35 |
| Висмут | -72 |
Полные термоэлектрические уравнения
Часто в работе реального термоэлектрического устройства задействовано несколько из перечисленных выше эффектов. Эффект Зеебека, эффект Пельтье и эффект Томсона могут быть собраны вместе последовательным и строгим способом, описанным здесь; это также включает эффекты джоулева нагрева и обычной теплопроводности. Как указано выше, эффект Зеебека генерирует электродвижущую силу, приводящую к уравнению тока
- Jзнак равноσ(-∇V-S∇Т).{\ displaystyle \ mathbf {J} = \ sigma (- {\ boldsymbol {\ nabla}} VS \ nabla T).}
Чтобы описать эффекты Пельтье и Томсона, мы должны рассмотреть поток энергии. Если температура и заряд изменяются со временем, полное термоэлектрическое уравнение для накопления энергии,, имеет вид
е˙{\ displaystyle {\ dot {e}}}
- е˙знак равно∇⋅(κ∇Т)-∇⋅(V+Π)J+q˙доб,{\ displaystyle {\ dot {e}} = \ nabla \ cdot (\ kappa \ nabla T) — \ nabla \ cdot (V + \ Pi) \ mathbf {J} + {\ dot {q}} _ {\ text { ext}},}
где — теплопроводность . Первый член — , а второй член показывает энергию, переносимую токами. Третий член — это тепло, добавляемое от внешнего источника (если применимо).
κ{\ displaystyle \ kappa}q˙доб{\ displaystyle {\ dot {q}} _ {\ text {ext}}}
Если материал достиг устойчивого состояния, распределения заряда и температуры стабильны, поэтому и . Используя эти факты и второе соотношение Томсона (см. Ниже), уравнение теплопроводности можно упростить до
е˙знак равно{\ displaystyle {\ dot {e}} = 0}∇⋅Jзнак равно{\ Displaystyle \ набла \ cdot \ mathbf {J} = 0}
- -q˙добзнак равно∇⋅(κ∇Т)+J⋅(σ-1J)-ТJ⋅∇S.{\ displaystyle — {\ dot {q}} _ {\ text {ext}} = \ nabla \ cdot (\ kappa \ nabla T) + \ mathbf {J} \ cdot \ left (\ sigma ^ {- 1} \ mathbf {J} \ right) -T \ mathbf {J} \ cdot \ nabla S.}
Средний член — это джоулев нагрев, а последний член включает эффекты Пельтье ( на стыке) и Томсона ( в температурном градиенте). В сочетании с уравнением Зеебека для , это можно использовать для определения стационарных профилей напряжения и температуры в сложной системе.
∇S{\ displaystyle \ nabla S}∇S{\ displaystyle \ nabla S}J{\ displaystyle \ mathbf {J}}
Если материал не находится в устойчивом состоянии, полное описание должно включать динамические эффекты, такие как относящиеся к электрической емкости , индуктивности и теплоемкости .
Термоэлектрические эффекты выходят за рамки равновесной термодинамики. Они обязательно включают непрерывные потоки энергии. По крайней мере, они включают в себя три тела или термодинамические подсистемы, расположенные определенным образом, вместе с особым расположением окружения. Эти три тела — это два разных металла и область их соединения. Область сочленения представляет собой неоднородное тело, считающееся стабильным, не подвергающимся слиянию за счет диффузии вещества. Окрестности устроены так, чтобы поддерживать два резервуара температуры и два резервуара электрического тока. Для воображаемого, но не возможного термодинамического равновесия, теплопередача от горячего резервуара к холодному должна быть предотвращена за счет специально согласованной разности напряжений, поддерживаемой электрическими резервуарами, а электрический ток должен быть равен нулю. Фактически, для установившегося состояния должна быть хотя бы некоторая теплопередача или некоторый ненулевой электрический ток. Два режима передачи энергии — тепло и электрический ток — можно различить, когда есть три отдельных тела и определенное расположение окружения. Но в случае непрерывного изменения среды теплопередачу и термодинамическую работу нельзя однозначно различить. Это сложнее, чем часто рассматриваемые термодинамические процессы, в которых связаны всего две соответственно однородные подсистемы.
Физическое объяснение эффекта

Описанный термоэлектрический эффект является достаточно непростым явлением. Для его понимания рассмотрим систему, состоящую из медного и железного проводников, соединенных между собой
Обратим внимание на процессы, которые происходят в зоне контакта Cu-Fe, которая нагревается. Приобретая дополнительную кинетическую энергию, электроны в области нагрева создают более высокое «давление» электронного газа, поэтому стремятся убежать из нее к более холодному концу контура
Наоборот, контакт Cu-Fe, который охлаждается, вызывает потерю кинетической энергии носителей заряда, это ведет к снижению создаваемого ими давления в зоне контакта. Последний факт приводит к привлечению в холодную область свободных носителей заряда.
Если бы металлы в контакте были одинаковыми, то скорости дрейфа электронов в результате разности температур были бы одинаковыми, а их направления в каждом проводнике — противоположными, то есть никакой разности потенциалов бы не возникло. Но поскольку металлы имеют разную природу, то они различным образом реагируют на нагрев (изменение «давления» электронов и скорость их дрейфа разные для Fe и Cu). В этом и заключается причина появления ЭДС в зоне контакта.
Отметим, что при объяснении физики процесса использовалась аналогия с идеальным газом.
Направление возникающего термотока, а также его величина определяются природой металлов, разницей температур контактов, а также особенностями самой электрической замкнутой цепи.
Если рассмотреть физику процесса для пары металл-полупроводник, то она не будет отличаться от таковой для рассмотренной пары металл-металл. Приложение разности температур к двум контактам металла с полупроводником вызывает в последнем поток электронов (n-тип) или дырок (p-тип) от горячей области к холодной, что приводит к появлению разности потенциалов.
Если не поддерживать разность температур за счет отвода тепла от холодной зоны и его подвода к горячему контакту, то в цепи быстро устанавливается термодинамическое равновесие, и ток прекращает течь.
Применение
Элементы Пельтье можно использовать везде, где требуется охлаждение с небольшой разницей температур или без экономических требований. Термоэлектрические элементы используются, например, в холодных ящиках , в которых использование холодильной машины запрещены по соображениям пространства или не было бы выгодно , так как требуемая мощность охлаждения невелика. Разница температур внутри и снаружи просто возникает неконтролируемым образом. КПД низкий. Элементы Пельтье применяются в ситуациях, когда необходимо охлаждение с небольшой разницей температур или энергетическая эффективность охладителя не важна. Например, элементы Пельтье применяются в ПЦР-амплификаторах, малогабаритных автомобильных холодильниках, охлаждаемых банкетных тележках, применяемых в общественном питании, так как применение компрессорной холодильной установки в этом случае невозможно или нецелесообразно из-за габаритных ограничений, и, кроме того, требуемая мощность охлаждения невелика.
Кроме того, элементы Пельтье применяются для охлаждения устройств с зарядовой связью в цифровых фотокамерах. За счет этого достигается заметное уменьшение теплового шума при длительных экспозициях (например в астрофотографии). Многоступенчатые элементы Пельтье применяются для охлаждения приемников излучения в инфракрасных сенсорах.
Также элементы Пельтье часто применяются для охлаждения и термостатирования диодных лазеров с тем, чтобы стабилизировать длину волны излучения.
В приборах, при низкой мощности охлаждения, элементы Пельтье часто используются как вторая или третья ступень охлаждения. Это позволяет достичь температур на 30—40 градусов ниже, чем с помощью обычных компрессионных охладителей (до −80 °C для одностадийных холодильников и до −120 °C для двухстадийных).
Некоторые энтузиасты используют модуль Пельтье для охлаждения процессоров при необходимости экстремального охлаждения без азота. До азотного охлаждения использовали именно такой способ.
«Электрогенератор Пельтье» (более корректно было бы «
генератор зеебека », но неточное название устоялось) — модуль для генерации электричества, термоэлектрический генераторный модуль, аббревиатура GM, ТGM. Данный термогенератор состоит из двух основных частей:
- непосредственно преобразователь разницы температур в электричество на модуле Пельтье,
- источник тепловой энергии для нагрева преобразователя (например, газовая или бензиновая горелка, твердотопливная печь и т. д.)
КПД процесса
Это самый интересный и актуальный вопрос, который касается рассмотренного термоэлектрического эффекта. Если, приложив разность температур к цепи, можно получать электричество, тогда это явление можно использовать вместо распространенных генераторов, основанных на электромагнитной индукции. Этот вывод верен, если КПД эффекта Зеебека достаточно высок.
Для оценки КПД принято использовать следующее выражение:
Здесь ρ — удельное электрическое сопротивление, λ — коэффициент теплопроводности, Z — фактор эффективности термоэлектрического явления.
Понять это выражение несложно: чем больше коэффициент Зеебека, чем выше подвижность носителей заряда (меньше сопротивление) и чем меньше теплопроводность материала (она способствует выравниванию градиента температуры за счет переноса заряда и за счет движения фононов решетки), тем будет выше производительность цепи как генератора электричества.
Значения Z*T для металлов обычно невысоки, поскольку величина λ является большой. С другой стороны, изоляторы также нельзя использовать из-за их огромных значений ρ. Золотой серединой стало применение полупроводников.
В настоящее время для разных температур получены значения Z*T≈1, что означает следующее: примерно 10 % от затрачиваемого тепла переходит в электрическую энергию (КПД = 10 %). Чтобы этот эффект по эффективности выработки электричества мог конкурировать с современными способами его получения, необходимо разрабатывать материалы, для которых Z*T будет составлять 3-4.
КПД процесса
Удивительный факт перевода теплоты в электричество открывает большие возможности для применения этого явления. Тем не менее для его технологического использования важна не только сама идея, но и количественные характеристики. Во-первых, как было показано, возникающая ЭДС является достаточно маленькой. Эту проблему можно обойти, если использовать последовательное соединение большого числа проводников (что и делается в ячейке Пельтье, речь о которой пойдет ниже).

Во-вторых, это вопрос эффективности генерации термоэлектричества. И этот вопрос остается открытым по сей день. КПД эффекта Зеебека является чрезвычайно низким (порядка 10 %). То есть из всего затраченного тепла лишь одну десятую его можно будет использовать для совершения полезной работы. Многие лаборатории во всем мире стараются поднять этот КПД, что можно сделать, разработав материалы нового поколения, например, с помощью нанотехнологий.
Определение
Один из способов определения коэффициента Зеебека — это напряжение, возникающее при приложении к материалу небольшого температурного градиента и когда материал перешел в устойчивое состояние, при котором плотность тока повсюду равна нулю. Если разница температур Δ T между двумя концами материала мала, то коэффициент Зеебека материала определяется как:
- S знак равно — Δ V Δ Т {\ Displaystyle S = — {\ Delta V \ over \ Delta T}}
где Δ V — термоэлектрическое напряжение на выводах. (Подробнее о знаках Δ V и Δ T см. Ниже .)
Обратите внимание, что сдвиг напряжения, выраженный эффектом Зеебека, нельзя измерить напрямую, поскольку измеренное напряжение (путем присоединения вольтметра) содержит дополнительный вклад напряжения из-за градиента температуры и эффекта Зеебека в измерительных проводах. Напряжение вольтметра всегда зависит от относительных коэффициентов Зеебека для различных материалов.. В наиболее общем виде и технически коэффициент Зеебека определяется как часть электрического тока, вызванного температурными градиентами, как в векторном дифференциальном уравнении
В наиболее общем виде и технически коэффициент Зеебека определяется как часть электрического тока, вызванного температурными градиентами, как в векторном дифференциальном уравнении
- J знак равно — σ ∇ V — σ S ∇ Т {\ displaystyle \ mathbf {J} = — \ sigma {\ boldsymbol {\ nabla}} V- \ sigma S {\ boldsymbol {\ nabla}} T}
где — плотность тока , — электропроводность , — градиент напряжения, — градиент температуры. Описанный выше особый случай установившегося состояния при нулевом токе имеет место , что означает, что два члена электропроводности аннулированы, и поэтому J {\ Displaystyle \ scriptstyle \ mathbf {J}} σ {\ Displaystyle \ scriptstyle \ sigma} ∇ V {\ displaystyle \ scriptstyle {\ boldsymbol {\ nabla}} V} ∇ Т {\ displaystyle \ scriptstyle {\ boldsymbol {\ nabla}} T} J знак равно {\ Displaystyle \ scriptstyle \ mathbf {J} = 0} ∇ V знак равно — S ∇ Т . {\ displaystyle {\ boldsymbol {\ nabla}} V = -S {\ boldsymbol {\ nabla}} T.}
Подписать соглашение
Знак явно выражен в следующем выражении:
- S знак равно — V л е ж т — V р я грамм час т Т л е ж т — Т р я грамм час т {\ displaystyle S = — {\ frac {V _ {\ rm {left}} — V _ {\ rm {right}}} {T _ {\ rm {left}} — T _ {\ rm {right}}}}}
Таким образом, если S положительный, то конец с более высокой температурой имеет более низкое напряжение, и наоборот. Градиент напряжения в материале будет направлен против градиента температуры.
В эффекте Зеебека, как правило, преобладает вклад диффузии носителей заряда (см. Ниже), которая имеет тенденцию подталкивать носители заряда к холодной стороне материала до тех пор, пока не появится компенсирующее напряжение. В результате в полупроводниках p-типа (которые имеют только положительные подвижные заряды, электронные дырки ) S положительна. Точно так же в полупроводниках n-типа (которые имеют только отрицательные подвижные заряды, электроны ) S отрицательно. Однако в большинстве проводников носители заряда проявляют как дырочное, так и электронное поведение, и знак S обычно зависит от того, какой из них преобладает.
Связь с другими термоэлектрическими коэффициентами
Согласно второму соотношению Томсона (которое справедливо для всех немагнитных материалов в отсутствие внешнего магнитного поля) коэффициент Зеебека связан с коэффициентом Пельтье точным соотношением
Π {\ Displaystyle \ scriptstyle \ Pi}
- S знак равно Π Т , {\ displaystyle S = {\ frac {\ Pi} {T}},}
где — термодинамическая температура .
Т {\ displaystyle T}
Согласно первому соотношению Томсона и при тех же предположениях о магнетизме, коэффициент Зеебека связан с коэффициентом Томсона соотношением
K {\ displaystyle \ scriptstyle {\ mathcal {K}}}
- S знак равно ∫ K Т d Т . {\ Displaystyle S = \ int {\ frac {\ mathcal {K}} {T}} \, dT.}
Постоянная интегрирования такова , что при абсолютном нуле, в соответствии с требованиями теоремы Нернста .
S знак равно {\ displaystyle \ scriptstyle S = 0}
Ячейка Пельтье

Когда говорят о петентах на термо генераторные модули с эффектом Зеебека, то, конечно же, первым делом вспоминают про ячейку Пельтье. Она представляет собой компактное устройство (4x4x0,4 см), изготовленное из ряда последовательно соединенных проводников n- и p-типа. Изготовить ее можно своими руками. Эффекты Зеебека и Пельтье лежат в основе ее работы. Напряжения и токи, с которыми она работает, невелики (3-5 В и 0,5 A). Как было сказано выше, КПД ее работы очень маленький (≈10 %).
Применяется она для решения таких бытовых задач, как нагрев или охлаждение воды в кружке или подзарядка мобильного телефона.
Источник
Могут ли радиаторы генерировать собственный ток для вентилятора?
Поняв это, вы просто должны подумать о алюминиевом и медном радиаторе, где тепло излучается процессором или графическим процессором. У нас есть все компоненты: тепло, два металла и контур, образованный его сварными швами с двумя разными температурами: температура самого чипа и температура воздуха в ребрах.
Так почему же мощность не вырабатывается ни одним радиатором, отвечающим этим условиям? Не нужно полагаться на материнская плата функционировать и может регулироваться ШИМ как единственная паразитная функция, как обычно делают насосы AIO.
Теория творила бы чудеса, если бы не два фактора: требуются бесконечно лучшие припои, чем сегодня, что сделало бы цену каждого радиатора более дорогой, и, во-вторых, эффект Зеебека крайне неэффективно .
Для реализации этой идеи и оставления названных затрат в стороне потребуется огромное количество тепла, чтобы обеспечить стабильные милливольты.
Если нам нужен один или два вольта, то речь идет о температурах, более типичных для литейного цеха металла, чем для ПК. С учетом степеней, которые получает текущий процессор или графический процессор, нам вряд ли придется преодолевать несущую силу, без оси и без лопастей, поэтому промышленность, хотя и учитывает этот эффект при разработке своих продуктов, поддерживает вентиляторы с соответствующими им ШИМ. или 3-контактный по понятным причинам.
Ближайшая индустрия ПК стала использовать тепло в качестве источника движения вентилятора Мотор Стирлинга и это был провал, что мы увидим в другой статье.
Полные термоэлектрические уравнения [ править ]
Часто в работе реального термоэлектрического устройства задействовано несколько из перечисленных выше эффектов. Эффект Зеебека, эффект Пельтье и эффект Томсона могут быть собраны вместе последовательным и строгим способом, описанным здесь; это также включает эффекты джоулева нагрева и обычной теплопроводности. Как указано выше, эффект Зеебека генерирует электродвижущую силу, приводящую к уравнению тока
- J=σ(−∇V−S∇T).{\displaystyle \mathbf {J} =\sigma (-{\boldsymbol {\nabla }}V-S\nabla T).}
Чтобы описать эффекты Пельтье и Томсона, мы должны рассмотреть поток энергии. Если температура и заряд меняются со временем, полное термоэлектрическое уравнение для накопления энергии,,, имеет вид e˙{\displaystyle {\dot {e}}}
- e˙=∇⋅(κ∇T)−∇⋅(V+Π)J+q˙ext,{\displaystyle {\dot {e}}=\nabla \cdot (\kappa \nabla T)-\nabla \cdot (V+\Pi )\mathbf {J} +{\dot {q}}_{\text{ext}},}
где — теплопроводность . Первый член — , а второй член показывает энергию, переносимую токами. Третий член — это тепло, добавляемое от внешнего источника (если применимо).
κ{\displaystyle \kappa }q˙ext{\displaystyle {\dot {q}}_{\text{ext}}}
Если материал достиг устойчивого состояния, распределения заряда и температуры стабильны, поэтому и . Используя эти факты и второе соотношение Томсона (см. Ниже), уравнение теплопроводности можно упростить до
e˙={\displaystyle {\dot {e}}=0}∇⋅J={\displaystyle \nabla \cdot \mathbf {J} =0}
- −q˙ext=∇⋅(κ∇T)+J⋅(σ−1J)−TJ⋅∇S.{\displaystyle -{\dot {q}}_{\text{ext}}=\nabla \cdot (\kappa \nabla T)+\mathbf {J} \cdot \left(\sigma ^{-1}\mathbf {J} \right)-T\mathbf {J} \cdot \nabla S.}
Средний член — это джоулев нагрев, а последний член включает эффекты Пельтье ( на стыке) и Томсона ( в температурном градиенте). В сочетании с уравнением Зеебека для , это можно использовать для определения стационарных профилей напряжения и температуры в сложной системе.
∇S{\displaystyle \nabla S}∇S{\displaystyle \nabla S}J{\displaystyle \mathbf {J} }
Если материал не находится в устойчивом состоянии, полное описание должно включать динамические эффекты, такие как относящиеся к электрической емкости , индуктивности и теплоемкости .
Термоэлектрические эффекты выходят за рамки равновесной термодинамики. Они обязательно включают непрерывные потоки энергии. По крайней мере, они включают в себя три тела или термодинамические подсистемы, расположенные определенным образом, вместе с особым расположением окружения. Эти три тела — это два разных металла и область их соединения. Область сочленения представляет собой неоднородное тело, считающееся стабильным, не подвергающимся амальгамации за счет диффузии вещества. Окрестности устроены так, чтобы поддерживать два резервуара температуры и два резервуара электрического тока. Для воображаемого, но не возможного термодинамического равновесия теплоПередача из горячего резервуара в холодный резервуар должна быть предотвращена за счет специально согласованной разницы напряжений, поддерживаемой электрическими резервуарами, а электрический ток должен быть равен нулю. Фактически, для установившегося состояния должна быть хотя бы некоторая теплопередача или некоторый ненулевой электрический ток. Два режима передачи энергии — тепло и электрический ток — можно различить, когда есть три отдельных тела и определенное расположение окружения. Но в случае непрерывного изменения среды теплопередачу и термодинамическую работу нельзя однозначно различить. Это сложнее, чем часто рассматриваемые термодинамические процессы, в которых связаны всего две соответственно однородные подсистемы.