Содержание
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Обновленное уравнение контура
Многие из выведенных уравнений относятся к переменному току. Если нам нужно получить усредненный по времени результат, то соответствующие переменные выражаются в СКЗ. К примеру, закон Ома передается как
Различные выражения для мощности переменного тока выглядят как:
Отсюда видно, что можно вывести среднюю мощность, основываясь на пиковом напряжении и токе.
Мощность переменного тока, основываясь на времени. Напряжение и ток пребывают в фазе, а их продукт колеблется между нулем и IV. Средняя мощность – (1/2) IV
СКЗ полезны, если напряжение меняется по форме сигнала, отличающегося от синусоидов (квадратные, треугольные или пилообразные волны).
Синусоидальные, квадратные, треугольные и пилообразные волны
Обзор
Электрический ток
Батарея
Измерения тока и напряжения в цепях
Микроскопический вид: скорость дрейфа
Сопротивление и резисторы
Закон Ома
Температура и сверхпроводимость
Сопротивление и удельное сопротивление
Зависимость сопротивления от температуры
Электрическая энергия и энергия
Переменные токи
Фазоры
Средниеквадратное значение корня
Меры предосторожности в домашнем хозяйстве
Электричество в мире
Люди и электрическая опасность
Проводимость нервов и электрокардиограммы
Электрическая активность в сердце
Что такое стандартное отклонение
Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.
Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.
Если есть значений, то:
- Когда мы имеем дело с генеральной совокупностью при вычислении дисперсии, мы делим на (как и было сделано в рассмотренном нами примере).
- Когда мы имеем дело с выборкой, при вычислении дисперсии делим на .
Все остальные расчеты производятся аналогично, в том числе и определение среднего.
Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:
Дисперсия выборки = мм2.
При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).
Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.
Расчет среднего и среднеквадратичного значений тока/напряжения
. . Вот здесь есть расширенный и углубленный вариант данной заметки . .
Будучи в очень недавнем прошлом яростным разработчиком всевозможных импульсных источников питания, интересовался всяким по данной теме. В частности – вычислением среднего (AVG, Average) и среднеквадратичного (действующего, эффективного, RMS) значений напряжений и (особенно) токов, живущих в разрабатываемом источнике. Для тех, кто не помнит/не знает – напомню определение среднеквадратичного значения тока/напряжения из Википедии:
Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока
Посему, хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. И про выпрямители во вторичной цепи – та же песня. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.
Или, например, делаем могучий источник с высоким КПД. Чтобы оптимально спроектировать обмотку магнитного элемента требуются уже среднее значение тока и среднеквадратичное значение переменной составляющей
В общем – куда ни плюнь, везде фигурируют RMS и AVG (среднее значение, а не антивирус, это важно). Поэтому было принято решение сделать себе некий инструмент, упрощающий жизнь разработчика импульсных источников питания
Вот этим инструментом я и хочу поделиться с общественностью – вдруг кому пригодится.
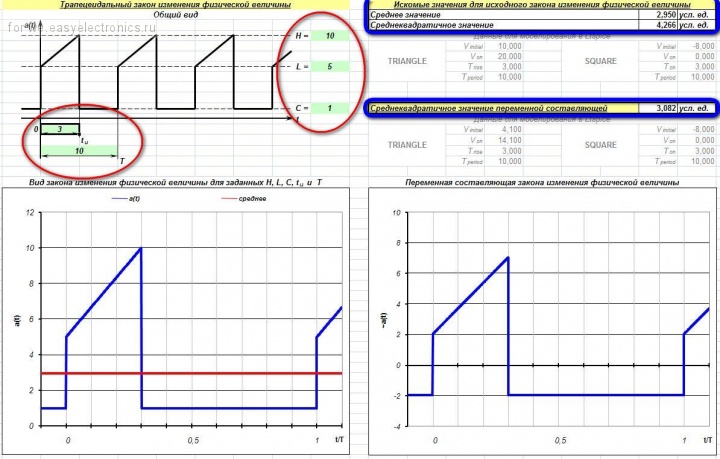
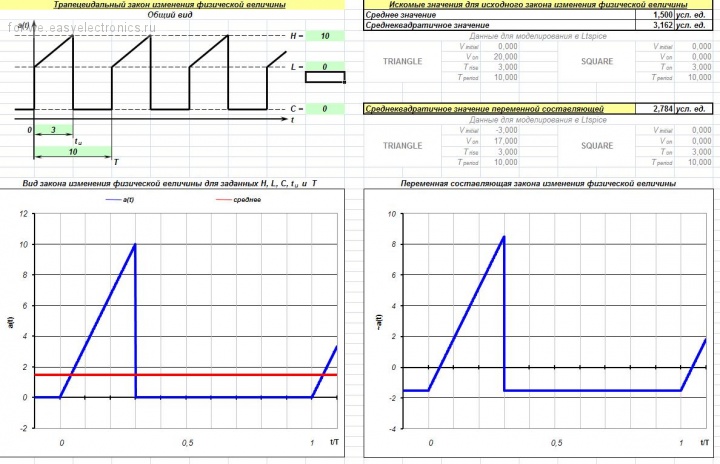
Как нетрудно заметить, данный инструмент («программа») представляет собой обычный Экселовский файл, поскольку в «компьютерном» программировании я вообще ничего не понимаю. В задачу рассматриваемой «программы» входит отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период) и отрисовка формы переменной составляющей заданного сигнала. Также «программа» умеет вычислять среднее и среднеквадратичное значения заданного сигнала и RMS-значение его переменной составляющей. Исходные данные вводятся слева в ячейки, выделенные зеленым цветом (на рисунке обведены красным). Рассчитанные значения AVG и RMS, а также среднеквадратичное значение переменной составляющей заданного сигнала отображаются в правой стороне экрана (обведены синим). Ну а картинки рисуются в нижней части экрана: слева – исходный сигнал, справа – его переменная составляющая.
В нагрузку к «программе» идет короткая заметка, в которой выводятся (а не берутся невесть откуда) расчетные формулы для основных форм сигналов в импульсных источниках питания (трапеции, прямоугольника, треугольника, пилы). Также в этой короткой заметке рассмотрен пример расчета AVG и RMS значений сложного сигнала.
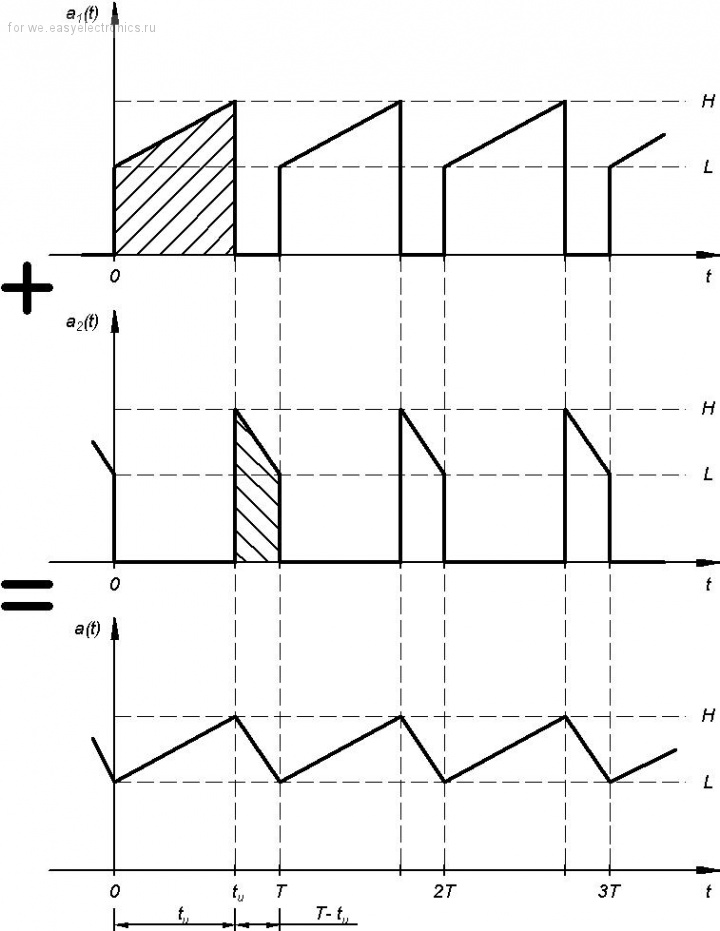
Почему в качестве основы взята именно трапеция? Потому, что из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник
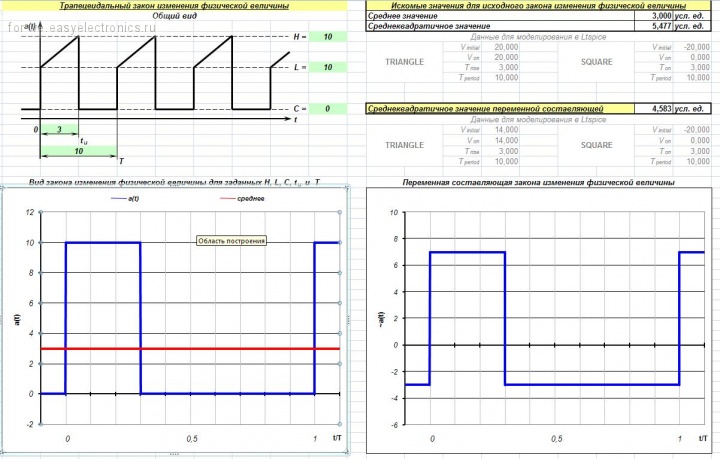
А уж на основе этих базовых сигналов можно сляпать и пилу
и даже то, что творится на вторичке пушпула:
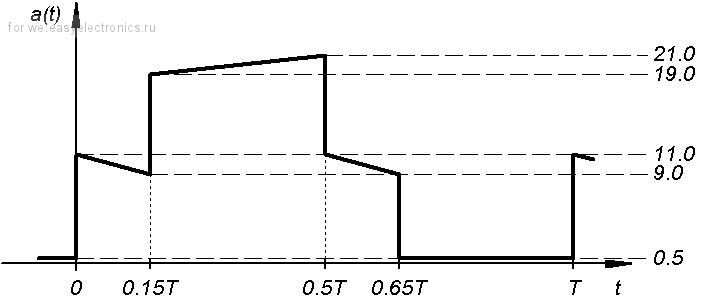
И еще много чего. Пример же расчета среднего и среднеквадратичных значений для сложных (т.е., составленных из простейших) сигналов, повторюсь, есть в короткой заметке-нагрузке. Хотя, если кого-то заинтересует данный аспект, могу впоследствие осветить его и в этом топике.
Вот, в принципе, и всё описание представленной «программы». Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!
Определение
Среднеквадратичное значение (СКЗ) – статическая мера переменной величины. Это полезно, если функция чередует положительные и отрицательные показатели (синусоиды). Перед нами квадратный корень из среднего арифметического квадратов. В случае набора значений n (x1, x2, …., xn) СКЗ определяется по формуле:
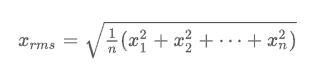
Соответствующая формула для непрерывной функции f (t), вычисленной на интервале T1 ≤ t ≤ T2:
Среднеквадратичное значение тока для функции в течение всего времени:
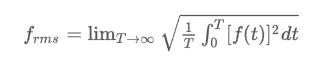
Среднеквадратичное значение напряжения за время периодической функции приравнивается к СКЗ одного периода.
Действующее значение напряжения и тока
В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.
P = I²R; A = I²Rt; P = U²/R; A = U²t/R
Величина постоянного напряжения или тока является его среднеквадратичным значением. Среднеквадратичное значение переменного тока равно величине постоянного тока, действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода. Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности P avg или работы A avg, пропорциональное квадрату значения тока. Так же среднеквадратичное значение переменного напряжения за период равносильно по своему воздействию на активную нагрузку такому же значению постоянного напряжения.
Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.
Величину переменного напряжения или тока, в большинстве случаев, выражают его среднеквадратичным значением и измеряют приборами электромагнитного типа или специальными среднеквадратичными измерителями – True RMS.
Примечание: Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках. Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению. Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.
Среднеквадратичное значение (RMS) для дискретных данных
Как преобразовать приведенную выше формулу во что-то, что можно применить к дискретным данным? Другими словами, как мы можем вычислить среднеквадратичное значение оцифрованного сигнала?
Давайте посмотрим на это так: сначала, вместо функции (например, x(t)), мы возводим в квадрат отдельные значения (например, x, x, x и т.д.). Затем, когда мы переходим от сигнала, непрерывного по времени, к сигналу, дискретному времени, интегрирование становится суммированием, а временной интервал становится «интервалом» точек данных, то есть количеством точек данных, которые были суммированы. И в конце у нас идет квадратный корень, который не меняется.
Таким образом, мы можем записать наш расчет среднеквадратичного значения (RMS), дискретного по времени, следующим образом:
\^2 + x^2 + … + x^2)}\]
Это начинает казаться знакомым? Мы возводим значения в квадрат, суммируем их, делим на количество значений и извлекаем квадратный корень.
Есть только два отличия между этой процедурой и процедурой, которую мы используем для расчета стандартного отклонения:
- В случае RMS мы делим на N; со стандартным отклонением мы (обычно) делим на N–1. Мы можем игнорировать эту разницу, потому что использование N–1 – это просто попытка компенсировать небольшой размер выборки (для получения дополнительной информации смотрите предыдущую статью).
- В случае RMS мы возводим в квадрат точки данных; в случае стандартного отклонения мы возводим в квадрат разницу между каждой точкой данных и средним значением.
Если мы пытаемся установить связь между среднеквадратичным значением и стандартным отклонением, второе различие может показаться решающим.
Однако учтите следующее: если среднее значение равно нулю, как это часто бывает в электрических сигналах, не будет никакой разницы между вычислением RMS и вычислением стандартного отклонения. Другими словами, для сигнала без смещения по постоянному току стандартное отклонение сигнала также равно среднеквадратичному значению.
Ссылки [ править ]
- ^
- Томпсон, Сильванус П. (1965). . Международное высшее образование Macmillan. п. 185. ISBN
- Джонс, Алан Р. (2018). . Рутледж. п. 48. ISBN
- Картрайт, Кеннет V (осень 2007 г.). . Технологический интерфейс . 8 (1): 20 стр.
-
Nastase, Адриан С. . MasteringElectronicsDesign.com . Проверено 21 января 2015 года .
- . Keysight . Keysight . Проверено 15 января 2019 .
- Если AC = a и BC = b . OC = AM для a и b , а радиус r = QO = OG. Используя теорему Пифагора , QC² = QO² + OC² ∴ QC = √ QO² + OC² = QM . Используя теорему Пифагора, OC² = OG² + GC² ∴ GC = √ OC² — OG² = GM . Используя подобные треугольники ,HCGC знак равно GCOC ∴ HC = GC²OC= HM .
-
Крис С. Бисселл; Дэвид А. Чепмен (1992). Передача цифрового сигнала (2-е изд.). Издательство Кембриджского университета. п. 64. ISBN
978-0-521-42557-5. -
Вайсштейн, Эрик В. . MathWorld .
- .
Можно ли изображать векторами действующие (эффективные) значения э. д. с. и токов?
Этот важный вопрос вызывает обычно недоумение. Ответить на него можно следующим образом.
Если нужно определять мгновенные значения синусоидальной величины, то удобнее брать вектор, изображающий ее максимальное значение, потому, что именно его проекция на ось дает мгновенные значения. Но в практической деятельности обычно имеют дело не с мгновенными, а с действующими 2 значениями, например говорят 220 В, понимая под этим действующее значение и не думая ни о максимальных значениях, которые на 41% больше, ни о других мгновенных значениях. Поэтому векторные диаграммы обычно строят для действующих значений. При этом углы сдвига фаз между током, э. д. с., напряжением и тому подобными видны совершенно отчетливо, а результаты сложения и вычитания векторов непосредственно получаются в действующих значениях, что удобно.
В распространенных формах волны
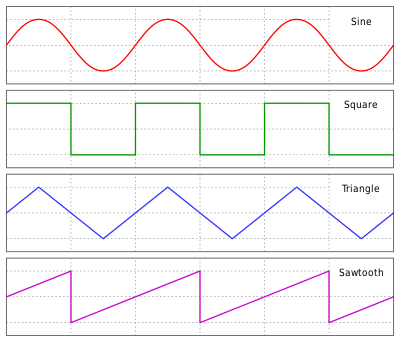
Синусоидальные , квадратные , треугольные и пилообразные формы сигналов. В каждом из них центральная линия находится на 0, положительный пик — на, а отрицательный — наузнак равноА1{\ displaystyle y = A_ {1}}узнак равно-А1{\ displaystyle y = -A_ {1}}
Прямоугольная импульсная волна с коэффициентом заполнения D, соотношением длительности импульса ( ) и периода (T); проиллюстрировано здесь с a = 1.τ{\ Displaystyle \ тау}
График зависимости напряжения синусоидальной волны от времени (в градусах), показывающий среднеквадратичное, пиковое (PK) и размах напряжения (PP).
Если форма волны представляет собой чистую синусоидальную волну , отношения между амплитудами (размах, пик) и среднеквадратичным значением фиксированы и известны, как и для любой непрерывной периодической волны. Однако это неверно для сигнала произвольной формы, который не может быть периодическим или непрерывным. Для синусоидальной волны с нулевым средним соотношение между среднеквадратичным значением и размахом амплитуды составляет:
- От пика до пика знак равно22×RMS≈2,8×RMS.{\ displaystyle = 2 {\ sqrt {2}} \ times {\ text {RMS}} \ примерно 2,8 \ times {\ text {RMS}}.}
Для других сигналов отношения не такие же, как для синусоидальных волн. Например, для треугольной или пилообразной волны
- От пика до пика знак равно23×RMS≈3.5×RMS.{\ displaystyle = 2 {\ sqrt {3}} \ times {\ text {RMS}} \ примерно 3,5 \ times {\ text {RMS}}.}
| Форма волны | Переменные и операторы | RMS |
|---|---|---|
| ОКРУГ КОЛУМБИЯ | узнак равноА{\ displaystyle y = A_ {0} \,} | А{\ displaystyle A_ {0} \,} |
| Синусоидальная волна | узнак равноА1грех(2πжт){\ Displaystyle у = А_ {1} \ грех (2 \ пи футов) \,} | А12{\ displaystyle {\ frac {A_ {1}} {\ sqrt {2}}}} |
| Квадратная волна | узнак равно{А1гидроразрыв(жт)<0,5-А1гидроразрыв(жт)>0,5{\ displaystyle y = {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <0,5 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,5 \ end {cases}} } | А1{\ Displaystyle A_ {1} \,} |
| Прямоугольная волна со смещением постоянного тока | узнак равноА+{А1гидроразрыв(жт)<0,5-А1гидроразрыв(жт)>0,5{\ displaystyle y = A_ {0} + {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <0,5 \\ — A_ {1} & \ operatorname {frac} (ft)> 0,5 \ конец {case}}} | А2+А12{\ displaystyle {\ sqrt {A_ {0} ^ {2} + A_ {1} ^ {2}}} \,} |
| узнак равно{гидроразрыв(жт)<0,25А10,25<гидроразрыв(жт)<0,50,5<гидроразрыв(жт)<0,75-А1гидроразрыв(жт)>0,75{\ displaystyle y = {\ begin {cases} 0 & \ operatorname {frac} (ft) <0,25 \\ A_ {1} & 0,25 <\ operatorname {frac} (ft) <0,5 \\ 0 & 0,5 <\ operatorname {frac} (футы) <0,75 \\ — A_ {1} & \ operatorname {frac} (футы)> 0,75 \ end {case}}} | А12{\ displaystyle {\ frac {A_ {1}} {\ sqrt {2}}}} | |
| Треугольник волна | узнак равно|2А1гидроразрыв(жт)-А1|{\ displaystyle y = \ left | 2A_ {1} \ operatorname {frac} (ft) -A_ {1} \ right |} | А13{\ displaystyle A_ {1} \ over {\ sqrt {3}}} |
| Пилообразная волна | узнак равно2А1гидроразрыв(жт)-А1{\ displaystyle y = 2A_ {1} \ operatorname {frac} (ft) -A_ {1} \,} | А13{\ displaystyle A_ {1} \ over {\ sqrt {3}}} |
| Пульсовая волна | узнак равно{А1гидроразрыв(жт)<Dгидроразрыв(жт)>D{\ displaystyle y = {\ begin {cases} A_ {1} & \ operatorname {frac} (ft) <D \\ 0 & \ operatorname {frac} (ft)> D \ end {cases}}} | А1D{\ displaystyle A_ {1} {\ sqrt {D}}} |
| Междуфазное напряжение | узнак равноА1грех(т)-А1грех(т-2π3){\ displaystyle y = A_ {1} \ sin (t) -A_ {1} \ sin \ left (t — {\ frac {2 \ pi} {3}} \ right) \,} | А132{\ displaystyle A_ {1} {\ sqrt {\ frac {3} {2}}}} |
куда:
|
В комбинациях сигналов
Формы сигналов, полученные путем суммирования известных простых сигналов, имеют среднеквадратичное значение, которое является корнем из суммы квадратов значений компонентных среднеквадратичных значений, если формы сигналов компонентов ортогональны (то есть, если среднее значение произведения одного простого сигнала на другой равно нулю. для всех пар, кроме самого времени сигнала).
- RMSВсегознак равноRMS12+RMS22+⋯+RMSп2{\ displaystyle {\ text {RMS}} _ {\ text {Total}} = {\ sqrt {{\ text {RMS}} _ {1} ^ {2} + {\ text {RMS}} _ {2} ^ {2} + \ cdots + {\ text {RMS}} _ {n} ^ {2}}}}
В качестве альтернативы, для сигналов, которые полностью положительно коррелированы или «синфазны» друг с другом, их среднеквадратичные значения суммируются напрямую.
Связь с другой статистикой
Геометрический доказательство без слов который Максимум (а,б) > среднее квадратичное или же среднеквадратичное значение (QM) > среднее арифметическое (ЯВЛЯЮСЬ) > среднее геометрическое (GM) > гармоническое среднее (HM) > мин (а,б) двух положительных чисел а и б
Если Икс¯{ displaystyle { bar {x}}} это среднее арифметическое и σИкс{ displaystyle sigma _ {x}} это стандартное отклонение из численность населения или форма волны, тогда:
- Икссреднеквадратичное значение2=Икс¯2+σИкс2=Икс2¯.{ displaystyle x _ { text {rms}} ^ {2} = { overline {x}} ^ {2} + sigma _ {x} ^ {2} = { overline {x ^ {2}}} .}
Отсюда ясно, что среднеквадратичное значение всегда больше или равно среднему, поскольку среднеквадратичное значение также включает «ошибку» / квадратное отклонение.
Ученые-физики часто используют термин среднеквадратичное значение как синоним стандартное отклонение когда можно предположить, что входной сигнал имеет нулевое среднее значение, то есть относится к квадратному корню из среднего квадрата отклонения сигнала от заданной базовой линии или соответствия. Это полезно для инженеров-электриков при вычислении RMS сигнала «только переменный ток». Стандартное отклонение — это среднеквадратичное отклонение сигнала от среднего, а не около 0, Компонент постоянного тока удаляется (то есть RMS (сигнал) = stdev (сигнал), если средний сигнал равен 0).
Формула
RMSD оценщика по отношению к оцениваемому параметру определяется как квадратный корень из среднеквадратичной ошибки :
θ^{\ displaystyle {\ hat {\ theta}}}θ{\ displaystyle \ theta}
- RMSD(θ^)знак равноMSE(θ^)знак равноE((θ^-θ)2).{\ displaystyle \ operatorname {RMSD} ({\ hat {\ theta}}) = {\ sqrt {\ operatorname {MSE} ({\ hat {\ theta}})}} = {\ sqrt {\ operatorname {E} (({\ hat {\ theta}} — \ theta) ^ {2})}}.}
Для несмещенной оценки RMSD — это квадратный корень из дисперсии, известный как стандартное отклонение .
СКО прогнозируемых значений для моментов времени т о наличии регрессии по зависимой переменной с переменными , наблюдаемых в течение T времени, вычисляется для T различных предсказаний , как корень квадратный из среднего значения квадратов отклонений:
у^т{\ displaystyle {\ hat {y}} _ {t}} ут,{\ displaystyle y_ {t},}
- RMSDзнак равно∑тзнак равно1Т(у^т-ут)2Т.{\ displaystyle \ operatorname {RMSD} = {\ sqrt {\ frac {\ sum _ {t = 1} ^ {T} ({\ hat {y}} _ {t} -y_ {t}) ^ {2} } {T}}}.}
(Для регрессий по поперечным данным индекс t заменяется на i, а T заменяется на n .)
В некоторых дисциплинах RMSD используется для сравнения различий между двумя вещами, которые могут различаться, ни один из которых не принимается в качестве «стандарта». Например, при измерении средней разницы между двумя временными рядами и формула принимает вид
Икс1,т{\ displaystyle x_ {1, t}}Икс2,т{\ displaystyle x_ {2, t}}
- RMSDзнак равно∑тзнак равно1Т(Икс1,т-Икс2,т)2Т.{\ displaystyle \ operatorname {RMSD} = {\ sqrt {\ frac {\ sum _ {t = 1} ^ {T} (x_ {1, t} -x_ {2, t}) ^ {2}} {T }}}.}
Действующее значение переменного синусоидального тока[править]
Если все положительные и отрицательные мгновенные значения переменного синусоидального тока сложить, то их сумма будет равна нулю. Но если алгебраическая сумма всех мгновенных значений за период равна нулю, то и среднее значение этого тока за период также равно нулю: .Среднее значение синусоидального тока за период не может служить для измерения этого тока. Чтобы судить о величине переменного синусоидального тока, переменный ток сравнивают с постоянным током по их тепловому действию.Два тока, один из которых синусоидальный, а другой постоянный, эквивалентны по тепловому действию, если они, протекая по одинаковым сопротивлениям, за одинаковые отрезки времени выделяют одинаковое количество тепла.Действующее значение переменного синусоидального тока численно равно току постоянному, эквивалентному данному синусоидальному току, то есть выделяющему порознь с ним в одинаковом сопротивлении за одинаковый отрезок времени одинаковое количество тепла. Найдено экспериментально, а затем подтверждено теоретически, что величина действующего значения переменного синусоидального тока находится в строго определённой зависимости от амплитуды этого тока: , то есть действующее значение переменного синусоидального тока в раз меньше амплитуды этого тока.
Амперметр электромагнитной или электродинамической системы, включенный в цепь переменного синусоидального тока, показывает действующее значение тока.
Аналогично действующему значению переменного синусоидального тока можно говорить о действующем значении переменной синусоидальной электродвижущей силы или переменного синусоидального напряжения.Действующее значение напряжения в меньше его амплитуды: или .
Вольтметр электромагнитной или электродинамической системы, включенный в сеть переменного синусоидального тока, показывает действующее значение синусоидального напряжения.Например, в электрической розетке электрическое напряжение , так это действующее значение, амплитудное напряжение будет Вольт.
Данные формулы справедливы только для синусоидального тока, если импульсы будут треугольной, пилообразной, прямоугольной или иной формы — требуется другая методика вычисления.
Методом математического анализа можно определить среднее значение переменного синусоидального тока за половину периода, например за положительную полуволну синусоиды.
Среднее значение переменного синусоидального тока за половину периода равно
Также можно определить отношение действующего значения тока к среднему за половину периода (положительную полуволну). Это отношение для синусоидального тока равно:
Расчёт действующего значения
В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.
Запишем выражение U rms с применением интеграла функции U = U ampsin(t) для одного периода 2π :
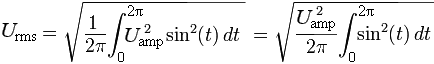
Вынесем U amp из под знака радикала. Воспользуемся табличным интегралом , перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:
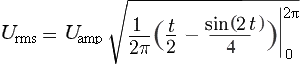
Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:
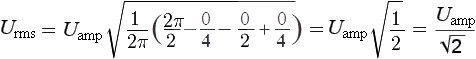
В результате решения в итоге получим:
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T для функции , представленной на рисунке:
Выразим U rms искомой функции с помощью определённого интеграла:
Используя табличный интеграл и формулу Ньютона-Лейбница, получаем:
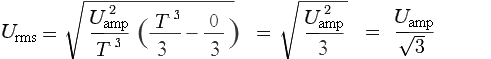
В итоге преобразований получим:
Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода. Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде. Например, для множества функций F1(t) , F2(t) , . , F n(t) в соответствующих им интервалах времени (0 – T1), (T1 – T2), . (T n – T), составляющих период T, действующее напряжение (RMS) определится выражением:
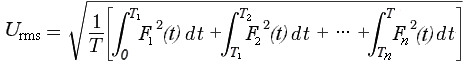
Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже, T и U amp имеют те же расчётные величины, что и в рассмотренном случае c функцией , а интегралы, определённые в интервалах, равных T, для квадратов используемых функций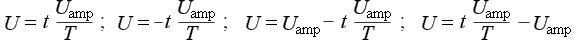 
, будут иметь одно и то же значение
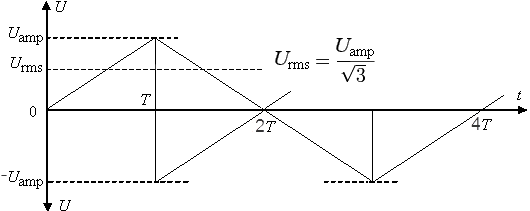
Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь среднеквадратичное значение .
В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью T i .
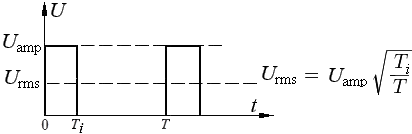
Выразим U rms одного периода T, как квадратный корень из среднеарифметического значения интегралов, определённых в интервалах 0 – T i и T i – T для квадратов всех значений периода.
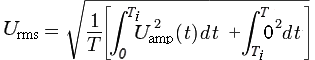
В результате получаем значение RMS, равное произведению амплитуды импульсов U amp на квадратный корень из коэффициента заполнения (T i / T).
В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.
Замечания и предложения принимаются и приветствуются!
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение ( ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
Среднее квадратическое отклонение простое:
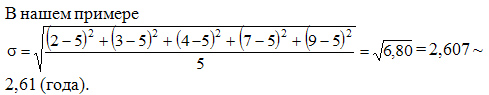
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение:
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Прикладное значение среднеквадратического отклонения
Среднеквадратическое отклонение от отклонений значений исследуемых данных находит широкое прикладное применение в метрологии, экспериментальной физике и статистике.
При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение величин будет являться оценкой ошибки измерений.
В свою очередь на основе минимизации среднеквадратических отклонений в 19 веке был разработан метод наименьших квадратов, который нашел широкое применение в таких областях как статистический, регрессионный анализ, обработка экспериментальных данных и вычислительная математика.
P.S. На этой странице используется Бета версия программы расчета среднеквадратического отклонения, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).
1. Среднее арифметическоезначение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:
aср.арифм =
a1+ a2+ …+ an
n
2. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:
σ 2 =
(a1 — acp)2 + (a2 — acp)2 + …+ (an — acp)2
n
3. Среднее линейное отклонение определяется как среднее от абсолютных значений отклонений каждого из ряда чисел от их среднего арифметического:
δ =
|a1 — acp| + |a2 — acp| + …+ |an — acp|
n
4. Коэффициент вариации ряда чисел — мера относительного разброса их значений; показывает, какую долю от среднего значения этой величины составляет её средний разброс. Исчисляется в процентах:
V =
σ
aср
× 100%
5. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Таким образом, размах вариации может быть представлен следующей формулой:
R = amax — amin
Приложения
- Минимизация MSE является ключевым критерием при выборе оценщиков: см. Минимальную среднеквадратичную ошибку . Среди несмещенных оценщиков минимизация MSE эквивалентна минимизации дисперсии, а оценщик, который делает это, является несмещенной оценкой с минимальной дисперсией . Однако смещенная оценка может иметь более низкую MSE; см. смещение оценки .
- В статистическом моделировании MSE может представлять разницу между фактическими наблюдениями и значениями наблюдений, предсказанными моделью. В этом контексте он используется для определения степени, в которой модель соответствует данным, а также для определения того, возможно ли удаление некоторых объясняющих переменных без значительного ущерба для предсказательной способности модели.
- В прогнозировании и прогнозировании , то оценка Шиповник является мерой успешности прогнозов на основе MSE.
Среднее квадратическое отклонение, методика расчета, применение.
Приближенный метод оценки колеблемости вариационного ряда — определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного признака в пределах вариационного ряда является среднее квадратическое отклонение (σ— сигма). Чем больше среднее квадратическое отклонение, тем степень колеблемости данного ряда выше.
Методика расчета среднего квадратического отклонения включает следующие этапы:
1. Находят среднюю арифметическую величину (Μ).
2. Определяют отклонения отдельных вариант от средней арифметической (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех отклонений равняется нулю.
3. Возводят каждое отклонение в квадрат d2.
4. Перемножают квадраты отклонений на соответствующие частоты d2*p.
5. Находят сумму произведений ( d2*p)
6. Вычисляют среднее квадратическое отклонение по формуле:
Значение среднего квадратичного отклонения:
1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.
2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.
Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.
Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат — частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.
Установлено, что при нормальном распределении признака:
— 68,3% значений вариант находится в пределах М1
— 95,5% значений вариант находится в пределах М2
— 99,7% значений вариант находится в пределах М3
3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М1 обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1 указывает на отклонение изучаемого параметра от нормы.
4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды
5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.
Величина среднего квадратического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратическое отклонение — именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv), представляющий собой относительную величину: процентное отношение среднего квадратического отклонения к средней арифметической.
Коэффициент вариации вычисляется по формуле:
Чем выше коэффициент вариации, тем большая изменчивость данного ряда. Считают, что коэффициент вариации свыше 30 % свидетельствует о качественной неоднородности совокупности.
StudFiles.ru
Интерпретация
Значение MSE, равное нулю, означающее, что оценщик предсказывает наблюдения параметра с идеальной точностью, является идеальным (но обычно невозможно).
θ^{\ displaystyle {\ hat {\ theta}}}θ{\ displaystyle \ theta}
Значения MSE могут использоваться для сравнительных целей. Две или более статистических моделей можно сравнить с использованием их MSE — в качестве меры того, насколько хорошо они объясняют данный набор наблюдений: несмещенная оценка (оцененная на основе статистической модели) с наименьшей дисперсией среди всех несмещенных оценок является лучшей несмещенной оценкой или MVUE (Несмещенная оценка минимальной дисперсии).
Как анализ дисперсии, так и методы линейной регрессии оценивают MSE как часть анализа и используют оцененную MSE для определения статистической значимости изучаемых факторов или предикторов. Цель экспериментального плана состоит в том, чтобы построить эксперименты таким образом, чтобы при анализе наблюдений MSE была близка к нулю относительно величины по крайней мере одного из оцененных эффектов лечения.
При одностороннем дисперсионном анализе MSE можно вычислить путем деления суммы квадратов ошибок и степени свободы. Кроме того, значение f представляет собой отношение среднего квадрата обработки и MSE.
MSE также используется в нескольких методах пошаговой регрессии как часть определения того, сколько предикторов из набора кандидатов включить в модель для данного набора наблюдений.
