Электрический заряд. закон кулона

Воздействуем на движущийся заряд

Магниты влияют на электрический ток: они создают силу, которая действует на движущиеся в нем электрические заряды. Однако электрические заряды должны двигаться, иначе не будет силы, действующей на них со стороны магнитного поля.

Как это происходит, показано на рис. 18.3, где на заряд, движущийся со скоростью \( \mathbf{v} \), через магнитное поле, показанное на рисунке вектором магнитной индукции \( \mathbf{B} \), действует сила со стороны этого магнитного поля. (Подробнее о векторах можно узнать в главе 4.)

(Магнитное поле в точке пространства определяется такой векторной величиной, как магнитная индукция \( \mathbf{B} \) в этой точке. Она играет ту же роль в магнетизме, что и напряженность электрического поля \( \mathbf{E} \) в электростатике. Направление поля в точке — это направление в ней вектора магнитной индукции, указываемое стрелкой компаса в этой точке. Линии магнитного поля — это линии, проведенные так, что касательные к ним в каждой точке указывают направление магнитной индукции в этой точке. — Примеч. ред.)

Магнитное поле создает силу, которая действует на движущийся заряд. Куда же направлена эта сила? Ответ можно увидеть на рис. 18.3, как и правило правой руки, с помощью которого вы сможете самостоятельно отвечать на этот вопрос.

Вариант 1. Если все пальцы правой руки, кроме большого, поместить вдоль магнитного поля (на рис. 18.3 оно показано вектором \( \mathbf{B} \)), а большой палец этой руки — в направлении скорости \( \mathbf{v} \) заряда, то сила, действующая на положительный заряд, должна выходить из ладони. Если заряд отрицательный, то сила направлена в противоположную сторону.

Вариант 2. Пальцы правой руки, кроме большого, поместите в направлении скорости v заряда, а затем сближайте их с ладонью, поворачивая на минимально возможный угол (меньший, чем 180°), пока они не будут указывать в направлении магнитного поля \( \mathbf{B} \). Тогда большой палец правой руки будет указывать в направлении действия силы.

Эти правила, возможно, напомнят вам сведения о моменте силы (его иногда называют вращающим моментом) (глава 10). Дело в том, что вектор силы выходит из плоскости, образованной векторами \( \mathbf{v} \) и \( \mathbf{B} \).

(В русскоязычной литературе принято использовать правило левой руки: если положить левую руку на проводник так, чтобы четыре пальца указывали направление тока, а линии магнитной индукции входили в ладонь, то отогнутый большой палец укажет направление силы, действующей на проводник. — Примеч. ред.)

Пользуясь любым из этих правил, вы сможете найти направление, в котором сила действует на движущийся заряд. Но насколько велика эта сила?

Что такое электрический заряд в каких единицах он измеряется

Простое объяснение понятия электрический заряд. Что это за величина, в чем она измеряется и как, собственно, ее измеряют.

В природе не все можно объяснить с точки зрения механики, МКТ и термодинамики, есть и электромагнитные явления, которые воздействуют на тело, при этом не зависят от их массы. Способность тел быть источником электромагнитных полей характеризуется физической скалярной величиной – электрическим зарядом

Его впервые вывели в законе Кулона в 1785 году, но обратили внимание на его существование еще до нашей эры. В этой статье мы простыми словами расскажем о том, что такое электрический заряд и как он измеряется

История открытий

Еще в древности было замечено, что если потереть янтарь о шелковую материю, то камень начнет притягивать к себе легкие предметы. Уильям Гильберт изучал эти опыты до конца XVI века. В отчете о проделанной работе предметы, которые могут притягивать другие тела, назвал наэлектризованными.

Следующие открытия в 1729 году сделал Шарль Дюфе, наблюдая за поведением тел при их трении об разные материи.

Таким образом он доказал существование двух видов зарядов: первые образуются при трении смолы о шерсть, а вторые – при трении стекла о шелк. Следуя логике, он назвал их «смоляными» и «стеклянными».

Шарлем Кулоном, портрет которого изображен ниже, был открыт закон, который впоследствии был назван Законом Кулона. Он описывал взаимодействие двух точечных зарядов. Также смог измерить величину и изобрел для этого крутильные весы, о которых мы расскажем позже.

И уже в начале прошлого века Роберт Милликен, в результате проведенных опытов, доказал их дискретность. Это значит, что заряд каждого тела равен целому кратному элементарного электрического заряда, а элементарным является электрон.

Теоретические сведения

Электрическим зарядом называется способность тел создавать электромагнитное поле. В физике раздел электростатики изучает взаимодействия неподвижных относительно выбранной инерциальной системы отчета зарядов.

В чем выражается взаимодействие

Электрические заряды притягиваются и отталкиваются друг от друга. Это похоже на взаимодействие магнитов. Всем знакомо, что если потереть линейку или шариковую ручку о волосы – она наэлектризуется.

Если в этом состоянии поднести её к бумаге, то она прилипнет к наэлектризованному пластику.

При электризации происходит перераспределение зарядов, так что на одной части тела их становится больше, а на другой меньше.

По этой же причине вас иногда бьёт током шерстяной свитер или другие люди, когда вы их касаетесь.

Вывод: электрические заряды с одним знаком стремятся друг к другу, а с разными – отталкиваются. Они перетекают с одного тела на другое, когда касаются друг друга.

Способы измерения

Существует ряд способов измерения электрического заряда, давайте рассмотрим некоторые из них. Измерительный прибор называется крутильными весами.

Весы Кулона – это крутильные весы его изобретения. Смысл заключается, в том, что в сосуде на кварцевой нити подвешена легкая штанга с двумя шариками на концах, и один неподвижный заряженный шарик. Вторым концом нить закреплена за колпак.

Неподвижный шарик вынимается, для того чтобы сообщить ему заряд, после этого нужно установить его обратно в сосуд. После этого подвешенная на нити часть начнет движение. На сосуде нанесена проградуированная шкала.

Принцип его действия отражен на видео.

https://youtube.com/watch?v=dNI9vZUscRs

Другой прибор для измерения электрического заряда – электроскоп. Он, как и предыдущие, представляет собой стеклянный сосуд с электродом, на котором закреплено два металлических листочка из фольги.

Заряженное тело подносят к верхнему концу электрода, по которому заряд стекает на фольгу, в результате оба листочка окажутся одноименно заряженными и начнут отталкиваться.

Величину заряда определяют по тому, насколько сильно они отклонятся.

Электрометр – еще один измерительный прибор. Состоит из металлического стержня и вращающейся стрелки. При прикосновении к электрометру заряженным телом, заряды стекают по стержню к стрелке, стрелка отклоняется и указывает на шкале определенную величину.

Напоследок рекомендуем просмотреть еще одно полезное видео по теме:

Ионизаторы воздуха положительно воздействуют на организм человека: ускоряют процесс доставки кислорода из воздуха к клеткам. Примером такого прибора является люстра Чижевского.

Теперь вы знаете, что такое электрический заряд и как его измеряют.

Материалы по теме:

Как перевести ватты в киловатты
Закон Джоуля-Ленца простыми словами
Что такое статическое электричество

Примеры явления

Само явление электризации было открыто еще в Древней Греции, когда заметили, что при натирании янтаря шерстью он начинает притягивать пыль, нитки, ворс. Это вещество по-гречески называется «электрон», отсюда и получили название все связанные с электричеством явления.

Положительно электризуется стекло при трении о шелк, отрицательно — эбонит при трении о шерсть. Все знают примеры электризации в быту, например, положительно заряжаются волосы, когда расчесываются пластиковой расческой, а сама расческа электризуется отрицательно. Заряжаются положительно стекло, бумага, шерсть, отрицательно — резина, силикон, пластик.

Статическое электричество дольше всего сохраняется на предметах, если воздух сухой. Влажный воздух проводит электричество, и предметы быстро перестают быть наэлектризованными. В присутствии комнатных растений, кипящего чайника, которые повышают влажность, статика на одежде и волосах появляется реже.

Реферат на тему: “Лазерные технологии и их использование” – виды, примеры и сферы применения

Известный пример электролизации — молния. Это электрический разряд, проскакивающий между разноименно заряженными облаками или между облаком и землей. Заряженные грозовые тучи могут вызывать электризацию различных предметов на земле из-за перераспределения зарядов на них.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Если массивную гирю поставить на пластину из изолятора и соединить с электрометром, а затем несколько раз ударить по ней куском меха, то гиря приобретёт отрицательный заряд и стрелка электрометра отклонится. При этом кусок меха приобретёт заряд

1) равный нулю
2) положительный, равный по модулю заряду гири
3) отрицательный, равный заряду гири
4) положительный, больший по модулю заряда гири

2. Два точечных заряда будут притягиваться друг к другу, если заряды

1) одинаковы по знаку и любые по модулю
2) одинаковы по знаку и обязательно одинаковы по модулю
3) различны по знаку, но обязательно одинаковы по модулю
4) различны по знаку и любые по модулю

3. На рисунках изображены три пары одинаковых лёгких заряженных шариков, подвешенных на шёлковых нитях. Заряд одного из шариков указан на рисунках. В каком(-их) случае(-ях) заряд второго шарика может быть отрицателен?

1) только А
2) А и Б
3) только В
4) А и В

4. Ученик во время опыта по изучению взаимодействия металлического шарика, подвешенного на шёлковой нити, с положительно заряженным пластмассовым шариком, расположенным на изолирующей стойке, зарисовал в тетради наблюдаемое явление: нить с шариком отклонилась от вертикали на угол \( \alpha \). На основании рисунка можно утверждать,что металлический шарик

1) имеет положительный заряд
2) имеет отрицательный заряд
3) не заряжен
4) либо не заряжен, либо имеет отрицательный заряд

5. Отрицательно заряженное тело отталкивает подвешенный на нити лёгкий шарик из алюминиевой фольги. Заряд шарика:

A. положителен
Б. отрицателен
B. равен нулю

Верными являются утверждения:

1) только Б
2) Б и В
3) А и В
4) только В

6. Металлический шарик 1, укреплённый на длинной изолирующей ручке и имеющий заряд \( +q \), приводят поочерёдно в соприкосновение с двумя такими же изолированными незаряженными шариками 2 и 3, расположенными на изолирующих подставках.

Какой заряд в результате приобретёт шарик 2?

1) 0
2) \( \frac{q}{4} \)
3) \( \frac{q}{3} \)
4) \( \frac{q}{2} \)

7. От капли, имеющей электрический заряд \( -2e \), отделилась капля с зарядом \( +e \). Каков электрический заряд оставшейся части капли?

1) \( -e \)
2) \( -3e \)
3) \( +e \)
4) \( +3e \)

8. Металлическая пластина, имевшая отрицательный заряд \( -10e \), при освещении потеряла четыре электрона. Каким стал заряд пластины?

1) \( +6e \)
2) \( +14e \)
3) \( -6e \)
4) \( -14e \)

9. К водяной капле, имевшей электрический заряд \( +5e \) присоединилась кайля с зарядом \( -6e \). Каким станет заряд объединенной капли?

1) \( +e \)
2) \( -e \)
3) \( +11e \)
4) \( -11e \)

10. На рисунке изображены точечные заряженные тела. Тела А и Б имеют одинаковый отрицательный заряд, а тело В равный им по модулю положительный заряд. Каковы модуль и направление равнодействующей силы, действующей на заряд Б со стороны зарядов А и В?

1) \( F=F_А+А_В \); направление 2
2) \( F=F_А-А_В \); направление 2
3) \( F=F_А+А_В \); направление 1
4) \( F=F_А-А_В \); направление 1

11. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.

1) Сила взаимодействия между электрическими зарядами тем больше, чем больше расстояние между ними.
2) При электризации трением двух тел их суммарный заряд равен нулю.
3) Сила взаимодействия между электрическими зарядами тем больше, чем больше заряды.
4) При соединении двух заряженных тел их общий заряд будет меньше, чем алгебраическая сумма их зарядов до соединения.
5) При трении эбонитовой палочки о мех заряд приобретает только эбонитовая палочка.

12. В процессе трения о шёлк стеклянная линейка приобрела положительный заряд. Как при этом изменилось количество заряженных частиц на линейке и шёлке при условии, что обмен атомами при трении не происходил? Установите соответствие между физическими величинами и их возможными изменениями при этом. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) количество протонов на шёлке
Б) количество протонов на стеклянной линейке
B) количество электронов на шёлке

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась

Тяни-толкай на основе электрических токов

Информация, полученная в этой главе до сих пор, просто удивительна, но как часто нам приходится иметь дело с движущимися зарядами? Возможно, кому-то и приходится работать с электронами, движущимися в вакууме, но большинство из нас сталкивается практически ежедневно не с одиночными движущимися зарядами, а с их группами, т.е. с электрическим током.

Сила, действующая на ток

Посмотрите на формулу силы, действующей на движущийся заряд:

где \( q \) — заряд, \( v \) — скорость, а \( B \) — значение магнитной индукции. Обладая полученными выше сведениями, нетрудно преобразовать эту формулу, одновременно поделив и умножив ее на \( t \) так, чтобы сама формула не изменилась:

Обратите внимание, что \( q/t \) — это заряд, проходящий через определенную точку за единицу времени, т.е. величина, известная под другим именем—электрический ток

Ну а \( vt \) — это всего лишь путь, который заряды проходят за время \( t \), поэтому прежнюю формулу можно переписать так:

Это сила, действующая на провод длины \( L \), через который проходит ток силой \( I \) в магнитном поле с индукцией \( \mathbf{B} \) и расположенный к этому полю под углом \( \theta \).

На рис. 18.6 показан провод, несущий ток силой \( I \) в магнитном поле с индукцией \( \mathbf{B} \) и расположенный к этому полю под углом 90°. Поскольку в физике за направление тока принято направление движения положительного заряда, то легко найти силу, действующую на провод. Пусть \( I \) = 2,0 А и \( B \) = 10 Тл. Какая сила будет действовать на провод длиной 1 м? Так как провод перпендикулярен к магнитному полю, то:

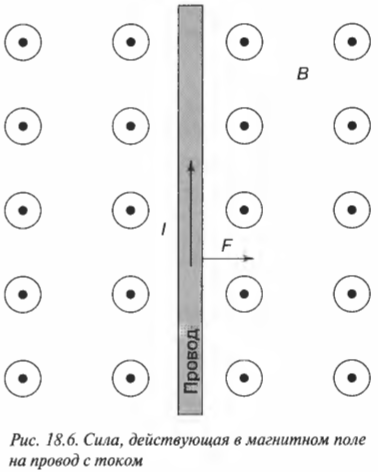
Силу, действующую на единицу длины, можно найти по формуле:

Подставляя в нее численные значения, получим:

Двадцать ньютонов на метр длины — это довольно заметная величина.

Момент силы, действующий на проводник с током

В электромоторах обычно используются постоянные магниты, а поля, создаваемые этими магнитами, пронизывают электрические катушки. Эти катушки могут вращаться благодаря тому, что приложенная к ним сила создает вращающий момент силы (см. главу 10). Как происходит это вращение, можно увидеть на рис. 18.7.

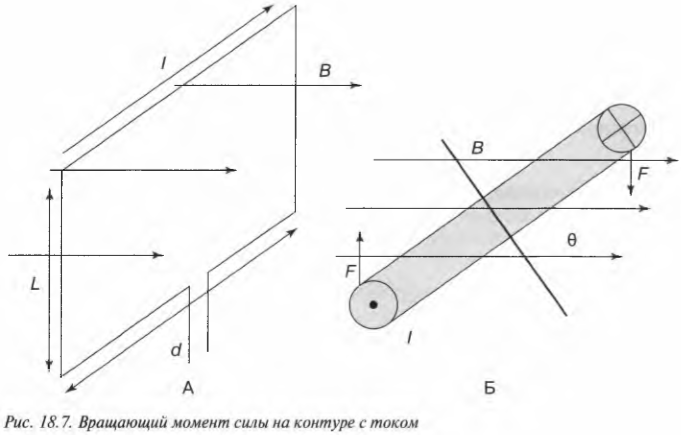
На схеме А показан контур с током в магнитном поле, которое создает действующие на контур силы, подробно показанные на схеме Б того же рисунка. Эти силы создают вокруг центральной оси два момента силы. Как показано на указанной схеме Б, плечо силы (см. главу 11) каждого момента силы выражается следующей формулой:

где \( d \) — это ширина контура. Каждый момент силы — это сила \( F \), умноженная на плечо силы, а сама сила \( F \) равна произведению силы тока \( I \) на длину контура \( L \) и на величину магнитной индукции \( B \). Так как имеется два момента силы, соответствующие двум сторонам контура, то получится общий момент сил \( M \):

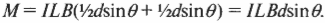
Получается интересный результат, так как произведение \( dL \) равно площади контура. Таким образом, для контура с площадью поперечного сечения \( A \) и углом \( \theta \). показанным на схеме Б, получим следующую формулу вращающего момента силы:

Впрочем, как правило, катушки содержат большое количество витков провода, т.е. контуров. Например, если катушка состоит из \( N \) витков провода, то для получения общего вращающего момента силы надо вращающий момент силы в одном витке (контуре) умножить на их количество \( N \):

Теперь можно найти общий вращающий момент силы проволочной катушки, состоящей из \( N \) витков, через каждый из которых проходит ток силой \( I \), имеет площадь \( A \) поперечного сечения и расположен к магнитному полю с индукцией \( B \) под углом \( \theta \). Ну наконец-то!

Рассмотрим следующую физическую задачу: найти максимально возможный вращающий момент силы, который будет испытывать в магнитном поле катушка из \( N \) витков. Чтобы найти этот момент, нужно выяснить, когда принимает максимальное значение множитель \( \sin\!\theta \). Это возможно в случае, когда \( \theta \) = 90°, т.е. \( \sin\!\theta \) = 1. Итак, получаем формулу максимального вращающего момента силы:

Например, каков максимальный вращающий момент силы для катушки, состоящей из 2000 витков, через которую проходит ток силой 5 А, имеющей площадь поперечного сечения 1,0 м2 и находящейся в магнитном поле с индукцией в 10 Тл? Ответ получить довольно легко:

Итак, максимальный вращающий момент силы равен 1,0·105 Н·м. Он имеет такое большое значение, потому что используется катушка с большим количеством витков. А если ограничиться одним-единственным витком, то максимальный вращающий момент силы будет равен всего 50 Н·м. Вот почему вращающиеся части электромоторов имеют так много витков провода.

Делимость электрического заряда. Электрон

В эксперименте с электрометрами металлическим стержнем часть заряда переносится от одного электрометра на другой. Из опыта видно, что заряд делится. Если коснуться стержня второго электрометра рукой, то заряд с него снимется, и распределится по всему телу (человеческое тело является хорошим проводником электричества). Если снова соединить приборы стержнем из металла, оставшийся заряд опять разделится. При повторении тех же шагов заряд каждый раз будет делиться. Кажется, что этот процесс будет происходить до бесконечности.

Заряды постепенно настолько уменьшаются, что электрометр уже не в состоянии их измерить. Уже очень точные опыты показали, что делить заряд до бесконечности нельзя, существует наименьший электрический заряд, который поделить уже нельзя. Называют его элементарным зарядом с абсолютной величиной e. Заряды измеряют в кулонах (Кл) в честь Шарля Кулона, французского физика.

Элементарным электрическим зарядом с отрицательным знаком обладает частица электрон (греч. «еlectron» – «янтарь»).

Ну, вот, собственно, и все! Вся природа у нас в кармане! Теперь нами понят ее главный принцип.

Как собрать следующий, третий по счету химический элемент в таблице Менделеева? Очень просто. Берем три протона, три нейтрона и три электрона. Нуклоны скатываем, как снежок, в одно ядро, вокруг запускаем три штучки электрончиков – и получаем литий. Литий – это уже не газ. Это уже легкий металл. Самый легкий металл на свете.

Вы, надеюсь, уже нашли водород, гелий и литий в таблице Менделеева…

А теперь поступим так. Найдите-ка в таблице наше родное и всеми горячо любимое золото. Стойте!.. Лучше, чтобы вы не листали книгу туда-сюда, я просто сам перенесу из таблицы Менделеева клеточку с золотом сюда. И расположу ее чуть ниже золотых слитков.

Золото. Согласитесь, посмотреть приятно! Эти бы слитки да в хорошие руки! А вот клеточка из таблицы Менделеева, где томится золото.

Мы видим тут значок золота – Au (аурум) – и две цифры. Верхняя – это порядковый номер элемента в таблице Менделеева. У золота № 79. Почему такой?

Отчего золото оказалось в периодической таблице элементов под номером 79?

Не знаете? А могли бы и догадаться! Вспомните, как мы строили первые три простейшие вещества. У первого, водорода – один протон и один электрон. У второго, гелия – по два. У третьего, лития – по три. Уловили закономерность? Порядковый номер – это количество протонов в ядре атома и электронов на орбите, вот и все! Если элемент стоит в таблице Менделеева пятым, то это только потому, что у него пять протонов в ядре, а вокруг кружатся 5 электронов.

А вторая цифра, которая внизу, что значит? Выглядит она страшно, но пугаться не стоит. Это атомная масса. Только выражена она не в килограммах или граммах, а в атомных единицах, где гирькой служит нуклон. 1 нуклон – это одна единица массы. Два нуклона – две единицы атомной массы. Крайне просто.

Примечания

Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — С. 17. — 656 с. — ISBN 5-9221-0227-3.
Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. 2 Теория поля. — 8-е изд., стереот. — М.: ФИЗМАТЛИТ, 2001. — 536 с. — ISBN 5-9221-0056-4 (Т. 2), Гл. 5 Постоянное электромагнитное поле, п. 38 Поле равномерно движущегося заряда, с 132
Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм. — М.: Наука, 1964. — Тираж 100 000 экз. — С. 33
Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. 3. Квантовая механика (нерелятивистская теория). — 5-е изд., стереот. — М.: Физматлит, 2002. — 808 с. — ISBN 5-9221-0057-2 (Т. 3), гл. 3 Уравнение Шредингера, п. 17 Уравнение Шредингера, с. 74
Бете Х. Квантовая механика. — пер. с англ., под ред. В. Л. Бонч-Бруевича, «Мир», М., 1965, Часть 1 Теория строения атома, Гл. 1 Уравнение Шредингера и приближённые методы его решения, с. 11
Пайерлс Р. Е. Законы природы. пер. с англ. под ред. проф. Халатникова И. М. , Государственное издательство физико-математической литературы, М., 1959, тир. 20000 экз., 339 с., Гл. 9 «Электроны при высоких скоростях», п. «Силы при больших скоростях. Другие трудности», c. 263
Novi Comm. Acad. Sc. Imp. Petropolitanae, v. IV, 1758, p. 301.
J. Priestley. The History and present state of Electricity with original experiments. London, 1767, p. 732.
Уиттекер Э. История теории эфира и электричества. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 76. — 512 с. — ISBN 5-93972-070-6.
Филонович С. Р. Кавендиш, Кулон и электростатика, М.: Знание. 1988, ББК 22.33 Ф53, гл. «Судьба закона», с. 48
Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 4 «Электростатика», п. 1 «Статика», с. 70-71;
Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 10 «Поле внутри полости проводника», с. 106—108;
Калашников С. Г.,
Электричество, М., ГИТТЛ, 1956, гл. III «Разность потенциалов», п. 34 «Точная проверка закона Кулона», с. 68—69; «Добавления», 1. «Теория опытов Кавендиша и Максвелла», с. 642—645;
E. R. Williams, J. E. Faller, H. A. Hill «New Experimental Test of Coulomb’s Law: A Laboratory Upper Limit on the Photon Rest Mass», Phys. Rev. Lett. 26, 721—724 (1971);
W. E. Lamb, R. C. Retherford. Fine Structure of the Hydrogen Atom by a Microwave Method (англ.) // Physical Review. — Т. 72, № 3. — С. 241-243.
↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 8 «Точен ли закон Кулона?», с. 103;
Берестецкий, В. Б., Лифшиц, Е. М., Питаевский, Л. П. Квантовая электродинамика. — Издание 3-е, исправленное. — М.: Наука, 1989. — С. 565-567. — 720 с. — («Теоретическая физика», том IV). — ISBN 5-02-014422-3.
Окунь Л. Б. Физика элементарных частиц. Изд. 3-е, М.: «Едиториал УРСС», 2005, ISBN 5-354-01085-3, ББК 22.382 22.315 22.3о, гл. 2 «Гравитация. Электродинамика», «Поляризация вакуума», с. 26-27;
«Физика микромира», гл. ред. Д. В. Ширков, М., «Советская энциклопедия», 1980, 528 с., илл., 530.1(03), Ф50, ст. «Эффективный заряд», авт. ст. Д. В. Ширков, стр. 496;
Яворский Б. М. «Справочник по физике для инженеров и студентов вузов» / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-e изд., перераб. и испр., М.: ООО «Издательство Оникс», ООО «Издательство Мир и образование», 2006, 1056 стр.: илл., ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (ООО «Издательство Мир и образование»), ISBN 985-13-5975-0 (ООО «Харвест»), УДК 530(035) ББК 22.3, Я22, «Приложения», «Фундаментальные физические постоянные», с. 1008;
Uehling E. A ., Phys. Rev., 48, 55, (1935)
Швебер С., Бете Г., Гофман Ф. Мезоны и поля. Том 1 Поля гл. 5 Свойства уравнения Дирака п. 2. Состояния с отрицательной энергией c. 56, гл. 21 Перенормировка, п. 5 Поляризация вакуума с 336
Мигдал А. Б. Поляризация вакуума в сильных полях и пионная конденсация// Успехи физических наук Т. 123— в. 3.— 1977 г., ноябрь.— с. 369—403;
Спиридонов О. П. Универсальные физические постоянные.— М.: Просвещение.— 1984.— с. 52-53;

Вычисляя магнитное поле в центре контура

Представьте себе, что на совещании группы разработчиков потребовалась ваша помощь. Взгляните на странное устройство, показанное на рис. 18.9. Вы видели что-либо подобное раньше?

“Конечно, — скажете вы. — Это ведь обычный контур с током.”

“Отлично, — ответят ваши коллеги. — Нам нужно вычислить магнитную индукцию в самом центре контура.”

“В самом центре?”

“Вот именно.”

“А мне заплатят?”

“Конечно.”

“Ладно, — скажете вы. — Магнитная индукция в самом центре контура с током определяется следующей формулой:

где \( N \) — количество витков контура, \( I \) — сила тока в нем, a \( R \) — радиус контура.”

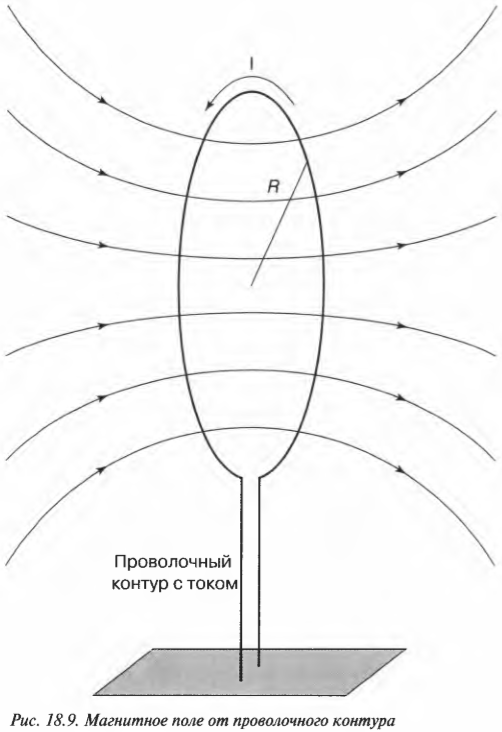
Пусть контур содержит не один виток, а 2000 витков, ток в нем равен 10 А, а радиус контура равен 10 см. Какова величина магнитной индукции в центре контура? Достаточно просто подставить численные значения в известную формулу:

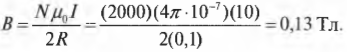
Итак, контур из 2000 витков создает магнитное поле с магнитной индукцией 0,13 Тл.

Свойства электрического заряда

Совокупность всех известных экспериментальных фактов позволяет выделить следующие свойства заряда:

Существует два рода электрических зарядов, условно названных положительными и отрицательными. Положительно заряженными называют тела, которые действуют на другие заряженные тела так же, как стекло, наэлектризованное трением о шелк.Отрицательно заряженными называют тела, которые действуют так же, как эбонит, наэлектризованный трением о шерсть. Выбор названия «положительный» для зарядов, возникающих на стекле, и «отрицательный» для зарядов на эбоните совершенно случаен.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Важным свойством электрического заряда является его дискретность . Это означает, что существует некоторый наименьший, универсальный, далее не делимый элементарный заряд, так что зарядq любого тела является кратным этому элементарному заряду: \(~q = N \cdot e\) , гдеN – целое число,е – величина элементарного заряда. Согласно современным представлениям, этот заряд численно равен заряду электронаe = 1,6∙10-19 Кл. Поскольку величина элементарного зарядавесьма мала, то для большинства наблюдаемых ииспользуемых на практике заряженных тел числоN очень велико, и дискретный характер изменения заряда не проявляется. Поэтому считают, что в обычных условиях электрический заряд тел изменяется практически непрерывно.
Закон сохранения электрического заряда .Внутри замкнутой системы при любых взаимодействиях алгебраическая сумма электрических зарядов остается постоянной: \(~q_1 + q_2 + \ldots + q_n = \operatorname{const}\) .Изолированной (или замкнутой) системой мы будем называть систему тел, в которую не вводятся извне и не выводятся из нее электрические заряды.

Нигде и никогда в природе не возникает и не исчезает электрический заряд одного знака. Появление положительного электрического заряда всегда сопровождается появлением равного по модулю отрицательного заряда. Ни положительный, ни отрицательный заряд не могут исчезнуть в отдельности, они могут лишь взаимно нейтрализовать друг друга, если равны по модулю.

Так элементарные частицы способны превращаться друг в друга. Но всегда при рождении заряженных частиц наблюдается появление пары частиц с зарядами противоположного знака. Может наблюдаться и одновременное рождение нескольких таких пар. Исчезают заряженные частицы, превращаясь в нейтральные, тоже только парами. Все эти факты не оставляют сомнений в строгом выполнении закона сохранения электрического заряда.

Причина сохранения электрического заряда до сих пор пока неизвестна.

Статическое электричество в быту

Пенопластовые шарики прилипли к кошачьей шерсти из-за статического электричества Статическое электричество широко распространено в обыденной жизни. Если, например, на полу лежит ковер из шерсти, то при трении об него человеческое тело может получить отрицательный электрический заряд, в то время как ковёр получит положительный. Другим примером может служить электризация пластиковой расчески, которая после причёсывания получает минус-заряд, а волосы получают плюс-заряд. Накопителем минус-заряда нередко являются полиэтиленовые пакеты, полистироловый пенопласт. Накопителем плюс-заряда может являться сухая полиуретановая монтажная пена, если её сжать рукой.

Когда человек, тело которого наэлектризовано, дотрагивается до металлического предмета, например, трубы отопления или холодильника, накопленный заряд моментально разрядится, а человек почувствует лёгкий удар током.

Электростатический разряд происходит при очень высоком напряжении и чрезвычайно низких токах. Даже простое расчёсывание волос в сухой день может привести к накоплению статического заряда с напряжением в десятки тысяч вольт, однако ток его освобождения будет настолько мал, что его зачастую невозможно будет даже почувствовать. Именно низкие значения тока не дают статическому заряду нанести человеку вред, когда происходит мгновенный разряд.

С другой стороны, такие напряжения могут быть опасны для элементов различных электронных приборов — микропроцессоров, транзисторов и т. п. Поэтому при работе с радиоэлектронными компонентами рекомендуется принимать меры по предотвращению накопления статического заряда.

Глава 3. как устроен атом и вообще весь мир