3 передаточные функции и частотные характеристики

Уравнения звеньев системы.

Целью
рассмотрения системы автоматического управления является решение одной из двух
задач: анализа или синтеза системы. При анализе системы требуется определить
свойства системы с заданными значениями параметров, при синтезе – создать
систему, удовлетворяющую заданным требованиям. В общем виде порядок исследования
в обоих случаях включает в себя математическое описание системы, исследование
ее установившихся и переходных режимов.

Математическое
описание, т.е. получение математической модели, начинается с разбиения системы
на звенья и описание этих звеньев. По уравнениямили характеристикам отдельных звеньев
составляют уравнения или определяют характеристики системыв целом, на основании которых ее исследуют.

Звеном
называют часть системы, которая осуществляет преобразование входной величины в
выходную. Звено обладает свойством однонаправленности, т.е. предыдущее звено
воздействует на последующее. Разбиение системы на звенья может не совпадать с
разбиением системы на функциональные элементы.

Звено
– это условно выделенный направленного действия преобразователь сигналов,
который может быть частью элемента или состоять из нескольких таких элементов.

Если
разбить систему на звенья направленного действия, то математическое описание
каждого звена может быть выполнено без учета его связей с другими звеньями
системы. При этом математическое описание всей системы в целом может быть
получено как совокупность составленных независимо друг от друга уравнений
звеньев системы и уравнений связи между звеньями.

Уравнениями
связи называют уравнения, отражающие характер передачи
воздействий между звеньями системы.

После
разбиения САУ на звенья направленного действия и получения математического
описания звеньев составляют структурную схему. Структурной схемой САУ
называется схема, показывающая, из каких звеньев состоит система и как эти
звенья соединены между собой. На структурной схеме звенья изображаются
прямоугольниками, а связи между звеньями и внешние воздействия – стрелками.
Каждому звену структурной схемы соответствует описывающее его уравнение или
характеристика. Получение структурной схемы является конечной целью
математического описания.

Различают
два вида характеристик звеньев: статические и динамические. Статическая
характеристика звена представляет собой зависимость между входной и выходной величинами в
установившемся режиме при разных постоянныхзначениях внешнего воздействия В общем случае эта зависимость
является нелинейной.

Если
на находящееся в некотором состоянии звено (систему) влияет возмущающее
воздействие, то звено начинает переходить в некоторое другое состояние. Характер
процесса перехода звена (системы) из одного состояния в другоеопределяется динамической
характеристикой звена (уравнением движения). Уравнение движения – это
дифференциальное уравнение, определяющее изменение во времени выходной величины
звена по заданному изменению во времени его выходной величины.

В
теории автоматического управления общее дифференциальное уравнение звена
(системы) принято записывать в следующем виде:

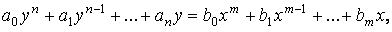
где
m и n – числа, показывающие высший порядок
производных от входной величиныи выходной величины ;

; ;

;;

В
большинстве случаев m<n. Числа m и n показывают высший порядок производных
от входной величины X и
выходной величины Y.

Если динамика звена описывается
линейным дифференциальным уравнением, то это звено называется линейным,
если дифференциальное уравнение нелинейное, то звено называют нелинейным.

Оптика

В оптике функция передачи модуляции указывает на возможность передачи оптического контраста.

Например, при наблюдении серии полос черно-белого света, нарисованных с определенной пространственной частотой, качество изображения может ухудшиться. Белая бахрома тускнеет, а черная становится ярче.

Передаточная функция модуляции на конкретной пространственной частоте определяется следующим образом:

MТF(ж)знак равноM(ямаграмме)M(sотырcе),{\ Displaystyle \ mathrm {MTF} (е) = {\ гидроразрыва {M (\ mathrm {image})} {M (\ mathrm {source})}},}

где модуляция (M) вычисляется из следующего изображения или яркости света:

Mзнак равноLМаксимум-LминLМаксимум+Lмин.{\ displaystyle M = {\ frac {L _ {\ max} -L _ {\ min}} {L _ {\ max} + L _ {\ min}}}.}

Обработка сигналов

Пусть будет вход общего линейного времени инвариантом системы и быть выходом, а двустороннее преобразование Лапласа от и быть
Икс(т){\ Displaystyle х (т)}у(т){\ Displaystyle у (т)}Икс(т){\ Displaystyle х (т)}у(т){\ Displaystyle у (т)}

Икс(s)знак равноL{Икс(т)} знак равноdеж ∫-∞∞Икс(т)е-sтdт,Y(s)знак равноL{у(т)} знак равноdеж ∫-∞∞у(т)е-sтdт.{\ Displaystyle {\ begin {align} X (s) & = {\ mathcal {L}} \ left \ {x (t) \ right \} \ {\ stackrel {\ mathrm {def}} {=}} \ \ int _ {- \ infty} ^ {\ infty} x (t) e ^ {- st} \, dt, \\ Y (s) & = {\ mathcal {L}} \ left \ {y (t) \ right \} \ {\ stackrel {\ mathrm {def}} {=}} \ \ int _ {- \ infty} ^ {\ infty} y (t) e ^ {- st} \, dt. \ end { выровнено}}}

Тогда выход связан с входом передаточной функцией как
ЧАС(s){\ Displaystyle H (s)}

Y(s)знак равноЧАС(s)Икс(s){\ Displaystyle Y (s) = H (s) X (s)}

и поэтому сама передаточная функция

ЧАС(s)знак равноY(s)Икс(s).{\ displaystyle H (s) = {\ frac {Y (s)} {X (s)}}.}

В частности, если сложный гармонический сигнал с синусоидальной составляющей с амплитудой , угловой частотой и фазой , где arg — аргумент|Икс|{\ displaystyle | X |} ω{\ displaystyle \ omega} аргумент⁡(Икс){\ Displaystyle \ arg (X)}

Икс(т)знак равноИксеjωтзнак равно|Икс|еj(ωт+аргумент⁡(Икс)){\ Displaystyle x (t) = Xe ^ {j \ omega t} = | X | e ^ {j (\ omega t + \ arg (X))}}

куда Иксзнак равно|Икс|еjаргумент⁡(Икс){\ Displaystyle X = | X | е ^ {j \ arg (X)}}

вводится в линейную инвариантную во времени систему, то соответствующий компонент на выходе:

у(т)знак равноYеjωтзнак равно|Y|еj(ωт+аргумент⁡(Y)),Yзнак равно|Y|еjаргумент⁡(Y).{\ Displaystyle {\ begin {align} y (t) & = Ye ^ {j \ omega t} = | Y | e ^ {j (\ omega t + \ arg (Y))}, \\ Y & = | Y | e ^ {j \ arg (Y)}. \ end {выравнивается}}}

Обратите внимание, что в линейной системе, не зависящей от времени, входная частота не изменилась, система изменила только амплитуду и фазовый угол синусоиды. Частотная характеристика описывает это изменение для каждой частоты с точки зрения усиления :
ω{\ displaystyle \ omega} ЧАС(jω){\ displaystyle H (j \ omega)}ω{\ displaystyle \ omega}

грамм(ω)знак равно|Y||Икс|знак равно|ЧАС(jω)|{\ Displaystyle G (\ omega) = {\ frac {| Y |} {| X |}} = | H (j \ omega) |}

и фазовый сдвиг :

ϕ(ω)знак равноаргумент⁡(Y)-аргумент⁡(Икс)знак равноаргумент⁡(ЧАС(jω)).{\ displaystyle \ phi (\ omega) = \ arg (Y) — \ arg (X) = \ arg (H (j \ omega)).}

Фазовой задержки (то есть, в зависимости от частоты величина задержки вводится в синусоиды с помощью передаточной функции) является:

τϕ(ω)знак равно-ϕ(ω)ω.{\ displaystyle \ tau _ {\ phi} (\ omega) = — {\ frac {\ phi (\ omega)} {\ omega}}.}

Групповая задержка (то есть, в зависимости от частоты величины задержки представлена огибающей синусоиды с помощью передаточной функции) определяется путем вычисления производной фазового сдвига по отношению к угловой частоте ,
ω{\ displaystyle \ omega}

τграмм(ω)знак равно-dϕ(ω)dω.{\ displaystyle \ tau _ {g} (\ omega) = — {\ frac {d \ phi (\ omega)} {d \ omega}}.}.

Передаточная функция также может быть показана с использованием преобразования Фурье, которое является лишь частным случаем двустороннего преобразования Лапласа для случая, когда .
sзнак равноjω{\ displaystyle s = j \ omega}

Общие семейства передаточных функций

Хотя любую систему LTI можно описать той или иной передаточной функцией, существуют определенные «семейства» специальных передаточных функций, которые обычно используются.

Некоторые общие семейства передаточных функций и их особые характеристики:

Фильтр Баттерворта — максимально ровный по полосе пропускания и полосе задерживания для данного порядка
Фильтр Чебышева (Тип I) — максимально плоский по полосе задерживания, более резкое срезание, чем фильтр Баттерворта того же порядка
Фильтр Чебышева (Тип II) — максимально плоская по полосе пропускания, более резкое срезание, чем фильтр Баттерворта того же порядка
Фильтр Бесселя — лучший импульсный отклик для заданного порядка, поскольку он не имеет пульсаций групповой задержки
Эллиптический фильтр — наиболее резкое срезание (самый узкий переход между полосой пропускания и полосой заграждения) для данного порядка
Оптимальный фильтр «L»
Фильтр Гаусса — минимальная групповая задержка; не дает перерегулирования ступенчатой функции
Фильтр песочных часов
Фильтр с приподнятым косинусом

Расчет — передаточная функция

Расчет передаточной функции С ( з) подробно рассмотрен в разд.

Методика расчет передаточных функций линий задержки с равноволновыми характеристиками группового времени совпадает с методикой, примененной при решении зад.

Методика расчета передаточных функций активных ЛС-филь-тров может быть использована при реализации корректирующих устройств систем числового программного управления станками. Коррекция систем ЧПУ осуществляется обычно на базе УПТ, построенных на интегральных микросхемах.

При расчете передаточных функций таких устройств целесообразно перейти от желаемой логарифмической частотной характеристики импульсной системы 1Ж ( А) к желаемой характеристике 1вж ( со) ее непрерывной части.

Предложенный метод расчета передаточных функций может найти широкое применение в расчетах переходных режимов и схем автоматического регулирования сложных объектов.

Если методика расчетов передаточных функций объектов регулирования в рассматриваемой области не разработана достаточно полно, то решение аналогичной задачи относительно регулирующей аппаратуры вызывает заметные трудности. Поэтому ниже описана методика определения передаточной функции регулятора методом графов.

Целью настоящей работы является расчет передаточных функций контактного аппарата с внутренним теплообменом по любому исследуемому каналу на примере окисления метанола в формальдегид на окисных катализаторах.

Ниже будет рассмотрена методика расчета передаточной функции применительно к этим формам кривой разгона объекта.

Эта подпрограмма предназначена для расчета передаточной функции и входного сопротивления линейной электрической цепи.

Выражения (4.18) являются основой для расчета передаточных функций UP методом стандартного z — преобразования.

На рис. 3.2 приведена укрупненная схема алгоритма расчета передаточной функции. Здесь блоки 3, 4, 5 выполняют действия, связанные с расчетами в i — й строке вычислений по схеме Ле-веррье — Фаддеева.

Таким образом, определены отдельные составляющие для расчета передаточных функций дозирующих и транспортирующих устройств, и, следовательно, в каждом конкретном случае свойства системы могут быть найдены.

Если структурная схема имеет перекрещивающиеся параллельные связи, то расчет передаточных функций усложняется.

Преобразования 1 — 4 используются в полном объеме для расчета передаточных функций / гграфов. Это объясняется тем, что, используя идеи Мейсона для анализа G-графов, не стремятся к получению полного аналитического выражения для Р ( с), а лишь определяют частные передаточные функции для путей и элементарных контуров, позволяющие выписать входящие в них дуги.

Способы коррекции.| Местная обратная связь.

Передаточные функции и характеристики разомкнутых систем.

Системы
автоматического управления в большинстве случаев являются замкнутыми. Однако
при их анализе и проектировании часто предварительно рассматривается разомкнутая
цепь звеньев, которая затем замыкается.

Различают
последовательное, параллельное и параллельное с обратной связью соединения
звеньев (рис.42).

Рис.42. Схемы соединения звеньев.

Последовательным
соединением звеньев называют такое соединение, когда выходная
величина предыдущего звена, является входной величиной последующего звена
(рис.42.а). Если последовательно соединяются звенья m и n, то .

Передаточная
функция всей цепи

Передаточные
функции звеньев

где-
изображение по Лапласу соответствующих переменных.

Если
перемножить правыеи левые части
полученных равенств получим

Поскольку
все промежуточные переменные при перемножении
сократятся, то

Передаточная
функция разомкнутой цепи последовательно соединенных звеньев равна произведению
передаточных функций всех звеньев.

Переходя
от передаточных функций к частотным характеристикам системы, т.е. полагая , получим

Представив
в виде,находим

;

Таким
образом, при последовательном соединении звеньев амплитудно-частотные
характеристики перемножаются, логарифмически амплитудно-частотные и фазовые
частотные характеристики складываются.

Рассмотрим
получение частотных характеристик разомкнутой цепи при последовательном
соединении звеньев. Пусть передаточная функция разомкнутой цепи

Причем
(при таком x
можно не учитывать «горб» АЧХколебательного
звена).

Логарифмическую
асимптотическую АЧХ можно построить непосредственно по передаточной функции.
ЛАЧХ является ломанной линией. При этом согласно характеристикам типовых
звеньев каждому сомножителю в знаменателе
соответствует точка излома характеристики при с последующим наклоном
минус 20 дБ/декаду, а каждому сомножителю такого же типа в числителе
соответствует точка излома также при , но с последующим наклоном плюс 20 дБ/декаду. Сомножителю
типа в знаменателе
соответствует излом характеристики при с наклоном минус 40
дБ/декаду.

Методика
построения ЛАЧХ (рис.43) сводится к следующему:

1)определение сопрягающих
частот типовых звеньев в порядке возрастания

; ; ; ; ;

2)
вычисление на частоте ординаты , где k –
общий коэффициент передачи разомкнутой системы. Через полученную точку проводят
низкочастотную асимптоту ЛАЧХ., представляющую собой при w<1 прямую с наклоном
минус 20r
дБ/декаду, где r —
число интегрирующих звеньев;

3)
изменение наклона ЛАЧХ на сопрягающих частотах по сравнению с тем наклоном,
который она имела до рассматриваемой частоты.

Рис.43. Частотные характеристики цепи последовательно
соединенных элементов.

Фазовая частотная характеристика (рис.43)
определяется по выражению:

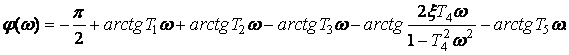
Параллельным
соединением звеньев называется такое соединение, когда на входе
всех звеньев подается одна и та же величина, а выходные сигналы суммируются
(рис.42.б). Если параллельно соединяются n звеньев, то входной сигнал

а
выходной сигнал

Переходя
к изображению и учитывая, что , получим

т.е.

Следовательно,

Таким
образом, при параллельном соединениизвеньев передаточные, переходные и весовые функции каждого звена
суммируются.

При
параллельном соединении звеньев с обратной связью обратная связь может быть
положительной, еслисигнал обратной
связи складывается с входным сигналом , или отрицательной, если сигнал обратной связи вычитается из (рис.42.в).

При
отрицательной обратной связи схема описывается следующим уравнением:

В
свою очередь определяется в соответствии с выражением

Подставив
значение в выражение для , получим

Решим
это уравнение относительно .

Отсюда

Передаточная
характеристика замкнутой системы при отрицательной обратно связи определяется в
соответствии с выражением

при
положительной обратной связи

Индивидуальные доказательства

Бернд Жирод, Рудольф Рабенштейн, Александр Стенгер: Введение в теорию систем . 4-е издание. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0 , стр.101 .
Бернд Жирод, Рудольф Рабенштейн, Александр Стенгер: Введение в теорию систем . 4-е издание. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0 , стр.7 .
Бернд Жирод, Рудольф Рабенштейн, Александр Стенгер: Введение в теорию систем . 4-е издание. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0 , стр.6 .
Джон Г. Проакис, Масуд Салехи: Разработка систем связи . 2-е издание. Prentice Hall, Upper Saddle River, NJ 2002, ISBN 0-13-095007-6 , стр.626 (английский).
Бернд Жирод, Рудольф Рабенштейн, Александр Стенгер: Введение в теорию систем . 4-е издание. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0 , стр.326 .
Бернд Жирод, Рудольф Рабенштейн, Александр Стенгер: Введение в теорию систем . 4-е издание. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0 , стр.102 .
Бернд Жирод, Рудольф Рабенштейн, Александр Стенгер: Введение в теорию систем . 4-е издание. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0 , стр.100 .
Бернд Жирод, Рудольф Рабенштейн, Александр Стенгер: Введение в теорию систем . 4-е издание. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0 , стр.303 .
Дуглас К. Линднер: сигналы и системы . McGraw-Hill, ISBN 0-07-116489-8 , стр. 294 f.

Техника управления

В контрольной технике и теории управления передаточная функция получена с помощью преобразования Лапласа .

Передаточная функция была основным инструментом, используемым в классической технике управления. Однако он оказался громоздким для анализа систем с множеством входов и множеством выходов (MIMO) и был в значительной степени вытеснен представлениями в пространстве состояний для таких систем. Несмотря на это, матрицу переноса всегда можно получить для любой линейной системы, чтобы проанализировать ее динамику и другие свойства: каждый элемент матрицы переноса является передаточной функцией, связывающей конкретную входную переменную с выходной переменной.

Полезное представление, связывающее пространство состояний и методы передаточной функции, было предложено Говардом Х. Розенброком и называется системной матрицей .

Основные характеристики звеньев и систем.

Передаточная
функция. Она характеризует изменение сигнала при его прохождении
через звено или систему (рис.29). В теории автоматического управления передаточные
функции устанавливают взаимосвязь между преобразованиями сигнала на входе и на
выходе звена или системы (преобразования Лапласа).

Рис.29. Структурная схема звена

Преобразование
Лапласа функции времени :

где — переменная
преобразования Лапласа,- символ
преобразования Лапласа.

Функция
называется оригиналом,
а — ее изображением.
При нулевых начальных условиях

;;.

Соответственно
, , . Применяя преобразование Лапласа к общему дифференциальному
уравнению, описывающему звено, при нулевых начальных условиях, получим

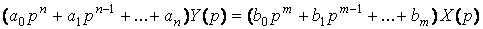
Передаточной
функцией звена или системы W(p) называется отношение изображений
Лапласа выходной и входной величин, т.е.

при
нулевых начальных условиях.

В
общем случае передаточная функция звена имеет вид

где M(p) и N(p) — полиномы степени m и n. ,

Если
известны передаточные функции отдельных звеньев системы, то можно получить
передаточную функцию всей системы в целом.

Переходная
функциязвена.
Переходнойфункцией h(t) называется реакция звена на единичное
ступенчатое воздействие (рис.30), т.е. переходной процесс на выходеy(t)при единичном скачке на входе звена. Следовательно

;

Рис.30.Переходная
функция звена.

Весовая
функция звена. Весовой функцией (импульсной переходной
функцией) называется реакция
звена или системы на единичный импульс (рис.31). Единичный импульс (импульсная
функция) представляет собой производную от единичной ступенчатой функции , и соответствует импульсу бесконечно большой амплитуды и
бесконечно малой длительности, возникающему в момент времени , так что его площадь равна единице, т.е.

Учитывая
это, получим ; , т.е. весовая функция представляет собой оригинал
передаточной функции.

Рис.31. Весовая функция звена.

Частотные
характеристики звена. Частотными характеристиками называются формулы
и графики, характеризующие реакцию звена на синусоидальное входное воздействие
в установившемся режиме.

Если
на вход звена подается величина (рис.32)

то
на выходе в установившемся режиме получается:

где- амплитуда, — фаза

Рис.32. Частотные характеристики звена.

Применяется
символическая запись синусоидальныхколебаний:

Подставив эти величины в уравнение звена,
получим

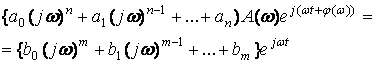
Откуда

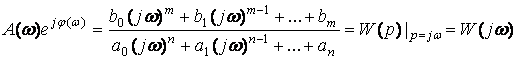
Отсюда
находим

представляет собой амплитудно-фазовую
частотную характеристику звена (АФЧХ). Иногда частотной
передаточной функцией звена, которая является комплексной функцией
от действительной переменной w. называется
соответственно амплитудно-частотной характеристикой звена (АЧХ), — фазовой частотной
характеристикой звена (ФЧХ).

Функцию
можно представить в
виде

где U(w) и V(w) –
соответственно вещественная и мнимая частотные характеристики.

Графически
АФЧХ изображается на комплексной плоскости в полярных координатах , как годограф функции (рис.33).

Рис.33. Амплитудно-фазовая частотная характеристика
звена.

Длина
вектора равна , а угол, образованный этим вектором с действительной
положительной полуплоскостью, равен .

Кроме
частотных характеристик используются логарифмические частотные характеристики —
логарифмические амплитудно-частотные (ЛАЧХ) и логарифмические фазовые
частотные (ЛФЧХ) характеристики.

ЛАЧХ
— это график зависимости от логарифма частоты lgw. При построении ЛАЧХ по оси абсцисс
откладывают частоту в логарифмическом масштабе, а по оси ординат L(w).

ЛФЧХ
— это график зависимости фазовойчастотной функции от логарифма частоты lgw. При его построении по оси абсцисс откладывают
частоту в логарифмическом масштабе, по оси ординат откладываютв градусах или
радианах.

За
единицу масштаба по оси абсцисс принимается декада – частотный интервал,
соответствующий изменению частоты в 10 раз. Ось ординат при построении этих
характеристик проводят через произвольную, удобную для рассматриваемой задачи,
точку, а не через точку w=0,
поскольку частоте w=0 соответствует
бесконечно удаленная точка.

Единицей L(w)
является децибел (дБ), равный одной десятой Бела. Бел -это единица десятичного логарифма
коэффициента усиления мощности сигнала, т.е. 1 Бел соответствует усилению
мощности в 10 раз. Поскольку мощность сигнала пропорциональна квадрату
амплитуды, а , то усиление в Белах, выраженное через отношение амплитуд,
равно . L(w)=20
дБ означает, что на данной частоте при прохождении сигнала через звено его амплитуда
увеличивается в 10 раз.

Устойчивость линейных систем

Общее решение линейного неоднородного
уравнения состоит из общего решения соответствующего однородного решения и
некоторого частного решения данного неоднородного уравнения.

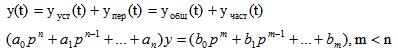
Таким образом, если САУ устойчива, y переходного процесса (Yпер(t)) при будут
затухающими.

Находим характеристический паленом, его корни
и в зависимости от того, к какому виду они относятся
определяем условия, при которых САУ будет устойчивой. Корни могут быть:

1) действительными кратными;

2) действительными и различными;

3) комплексными;

4) комплексными кратными.

Общее решение y(t) будет представлять паленом,
умноженный на сумму экспонент с заданными коэффициентами.

В случае комплексных корней, когда ,
каждой паре комплексно сопряженных корней будет соответствовать следующее
составляющая переходного процесса:

Если
хотя бы один корень >0, то система неустойчивая.

Система будет находиться на границе
устойчивости при наличии либо нулевого характеристического корня, либо пары
число мнимых корней. (a=0)

4. Критерий устойчивости Михайлова (вывод
— случай вещественных корней).

Формы представительства

Передаточная функция может быть задана либо в виде математической формулы, либо в виде графических кривых. При формальном представлении обычно выбирают между полиномиальным представлением , представлением его произведения или разложением на частичную дробь .

Графическое представление называется диаграммой Боде и состоит из описания усиления амплитуды и фазового сдвига входного сигнала.

Форма представительства	Обозначения в частотной области
многочлен	грамм(s)знак равнобмsм+бм-1sм-1+⋯+б1s+бапsп+ап-1sп-1+⋯+а1s+а{\ displaystyle G (s) = {\ frac {b_ {m} s ^ {m} + b_ {m-1} s ^ {m-1} + \ dotsb + b_ {1} s + b_ {0}}) {a_ {n} s ^ {n} + a_ {n-1} s ^ {n-1} + \ dotsb + a_ {1} s + a_ {0}}}}
Полюсные нули	грамм(s)знак равноk⋅(s-s,1)(s-s,2)⋯(s-s,м)(s-s∞,1)(s-s∞,2)⋯(s-s∞,п){\ Displaystyle G (s) = к \ cdot {\ frac {(s-s_ {0,1}) (s-s_ {0,2}) \ dotsm (s-s_ {0, m})} {( ss _ {\ infty, 1}) (ss _ {\ infty, 2}) \ dotsm (ss _ {\ infty, n})}}}
Частичная дробь	грамм(s)знак равноА.1s-s∞,1+А.2s-s∞,2+⋯+А.пs-s∞,п{\ displaystyle G (s) = {\ frac {A_ {1}} {s-s _ {\ infty, 1}}} + {\ frac {A_ {2}} {s-s _ {\ infty, 2}}} + \ dotsb + {\ frac {A_ {n}} {ss _ {\ infty, n}}}}

Полюса и нули функции очень легко считываются на дисплее продукта. Представление в дробных долях особенно подходит для обратного преобразования во временную область.

Виды ЧПФ

1. Амплитудно-фазовая частотная
характеристика (АФЧХ)

строится в комплексной плоскости,
представляет собой геометрическое место точек концов векторов (годограф),
соответствующее ЧПФ в комплексной форме. Т.к. w может
быть (+) и (–), то строится только положительная
ветвь, а отрицательная – зеркально отображается.

Построение АФФЧХ по вещественным и мнимым частям
– трудоемкая работа, проще строить ее, используя полярные координаты при
непосредственном вычислении модуля и фазы.

2. Амплитудно-частотная характеристика
(АЧХ)

Показывает, как звено пропускает сигнал
различной частоты.

3. Фазовая частотная характеристика (ФЧХ)

Показывает фазовые сдвиги, вносимые звеном на
различных частотах.

Вывод формул

Характер системы определяется
характеристическим полиномом:

p=jw, , где j – мнимая единица, w – угловая частота колебаний.

Произведем замену:

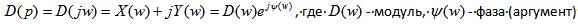
Пример

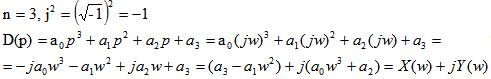
В X(w) содержатся
четные степени w, а в Y(w)
– нечетные.

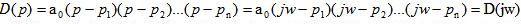
где каждая скобка – комплексное число, а при
умножении комплексных чисел аргументы складываются. Результирующий угол в
случае вещественных корней представляет собой .

Рассмотрим зависимость
между критерием Михайлова и знаками вещественных корней характеристического
уравнения при изменении w=[0,∞).

1. Предположим, что p1= – вещественное
отрицательное число. p1=-a1, a1>0

(jw-p1)=(jw+a1). Вектор OB при
займет положение π/2.

2. Предположим, что p1 – вещественное
положительное число. p1=a1, a1>0.

(jw-p1)=(jw-a1). Вектор OB при
займет положение -π/2

3. Если характеристическое уравнение имеет k корней с положительной вещественной частью, то им
соответствует сумма углов поворота, равная –k*π/2. Остальные (n-k) корней, имеющих отрицательные вещественные части,
будут иметь результирующий угол поворота: (n-k)*π/2.
Общий угол поворота вектора характеристического уравнения равен