Напряженность электрического поля — понятие, формула, единица измерения и значение

Как изобразить электрическое поле единичного заряда

Пусть неподвижный положительный точечный заряд создает в пространстве, окружающем его, электрическое поле. Нарисуем несколько векторов напряженности этого поля.

Красной точкой на рисунке обозначен заряд. А черным цветом обозначены точки, в которые помещали пробный заряд и измеряли поле.

Рис. 12. Можно изображать поле неподвижного заряда, располагая в пространстве векторы напряженности

По длине векторов можно сделать вывод, чем ближе к заряженному телу расположен пробный заряд, тем сильнее на него действует поле. Увеличив же расстояние между заряженным телом и пробным зарядом, заметим, что действие поля уменьшится.

Изображаем неоднородное электрическое поле силовыми линиями

Как видно, мы можем изобразить поле с помощью нарисованных в различных точках векторов напряженности. Однако, есть более удобный способ.

Присмотревшись к рисунку, можно заметить, что векторы напряженности, окружающие заряд, располагаются на некоторых прямых. Эти прямые обозначены пунктирными линиями на рисунке. Из называют линиями электрического поля, или линиями напряженности.

Примечание: Изображать электростатическое поле удобнее не с помощью векторов, а с помощью линий напряженности.

Если заряд единственный, а поблизости от него других зарядов нет, то его поле изображают радиально расходящимися во все стороны линиями.

Рис. 13. Набор силовых линий одиночного точечного заряда, это неоднородное поле

Линии положительных зарядов направлены от них, а линии отрицательных зарядов – к этим зарядам, так же, как векторы напряженности.

Мы помним, что вектор напряженности описывает силу, с которой поле, созданное зарядом может действовать на другие заряды. Поэтому, линии напряженности, так же, часто называют силовыми линиями поля.

Как выглядит поле двух взаимодействующих зарядов

Рассмотрим теперь поле взаимодействующих зарядов — положительного и отрицательного.

Рис. 14. Неоднородное поле двух точечных взаимодействующих зарядов

Как видно, линии взаимодействующих зарядов искривляются и, их конфигурация искажается.

Мы знаем, что поле одного точечного заряда неоднородное. Поле двух взаимодействующих зарядов, так же, неоднородное.

Теперь проведем обобщение, на рисунке неоднородное поле изображают:

• либо прямыми линиями, радиально расходящимися во все стороны от одиночного заряда, либо
• кривыми линиями, для взаимодействующих зарядов.

По мере удаления от зарядов расстояние между линиями будет увеличиваться. Чем дальше линии располагаются одна от другой в некоторой области пространства, тем слабее поле в этой области.

Кулоновская сила

Концепция Кулона характеризует взаимодействие между двумя зарядами, пребывающими в состоянии покоя. Она гласит: два недвижимых заряда отталкивают либо притягивают один другого с силой, которая прямо пропорциональна произведению величин зарядов, но обратна длине расстояния между этими зарядами во второй степени. Вместе с этим, сила взаимодействия пары зарядов не может измениться при присутствии третьего.

С помощью кулоновского принципа естествоиспытатель может отыскать состояние равновесия в ситуации свободного перемещения зарядов под воздействием силы другого типа, при котором заряды будут распределяться с постоянным коэффициентом. Сила Кулона предопределена третьим законом Ньютона, который утверждает, что заряды воздействуют один на другого с силами, которые равны по модулям, но противоположны по направлениям.

Суперпозиция полей

Закон Кулона и все вытекающие из него утверждения являются лишь основой для другого, более масштабного принципа – закона суперпозиции. Исходя из этого фундаментального утверждения, силы, которые действуют на заряды, каждый из которых располагается в конкретной точке объединённой системы, являют собой сумму сил, имеющих строгое направление и формируемых отдельными группами зарядов по отдельности и влияющих на заряды в конкретных точках.

Принцип суперпозиции полей

В отличие от закона Кулона, принцип суперпозиции может быть недостаточным в рамках некоторых квантовых явлений в электрическом поле.

Напряженность электрического поля

Недостаточно утверждать, что электрическое поле существует. Надо ввести количественную характеристику поля. После этого электрические поля можно будет сравнивать друг с другом и продолжать изучать их свойства. Электрическое поле обнаруживается по силам, действующим на электрический заряд. Можно утверждать, что мы знаем о поле все, что нужно, если будем знать силу, действующую на любой заряд в любой точке поля. Поэтому надо ввести такую характеристику поля, знание которой позволит определить эту силу.

Для изучения электрического поля будем использовать пробный заряд.

Под пробным зарядом будем понимать положительный точечный заряд, не изменяющий изучаемое электрическое поле.

Пусть электрическое поле создается точечным зарядом q. Если в это поле внести пробный заряд q₁, то на него будет действовать сила \(~\vec F\).

Обратите внимание, что в данной теме мы используем два заряда: источник электрического поля q0 и пробный заряд q1. Электрическое поле действует только на пробный заряд q1 и не может действовать на свой источник, т.е

на заряд q0.

Согласно закону Кулона эта сила пропорциональна заряду q₁:

Поэтому отношение силы, действующей на помещаемый в данную точку поля заряд q₁, к этому заряду в любой точке поля:

не зависит от помещенного заряда q₁ и может рассматриваться как характеристика поля. Эту силовую характеристику поля называют напряженностью электрического поля.

Подобно силе, напряженность поля – векторная величина, ее обозначают буквой \(~\vec E\) .

Напряженность поля равна отношению силы, с которой поле действует на точечный заряд, к этому заряду:

Сила, действующая на заряд q со стороны электрического поля, равна\ .

Если в точке А заряд q > 0, то векторы \(~\vec E_A\) и \(~\vec F_A\) направлены в одну и ту же сторону; при q < 0 эти векторы направлены в противоположные стороны.

От знака заряда q, на который действует поле, не зависит направление вектора \(~\vec E_A\), а зависит направление силы \(~\vec F_A\) (рис. 1, а, б).

В СИ напряженность выражается в ньютонах на кулон (Н/Кл).

Значение напряженности электрического поля, созданного:

• точечным зарядом q, на расстоянии r от заряда в точке C (рис. 2) равно

  \(~E = k \cdot \dfrac{|q|}{r^2}\) .

  Рис. 2

• сферой радиуса R с зарядом q, на расстоянии l от центра сферы в точке C (рис. 3), равно

  \(~E = k \cdot \dfrac{|q|}{l^2}\) , если l ≥ R;

  \(~E = 0\) , если l < R.

  Рис. 3

• заряженной бесконечной пластиной с поверхностной плотностью заряда σ, равно

  \(~E = \dfrac{|\sigma|}{2 \varepsilon_0}\) ,

  где \(~\sigma = \dfrac{q}{S}\) , q – заряд плоскости, S – площадь плоскости.

Принцип суперпозиции полей

А чему будет равна напряженность в некоторой точке электрического поля, созданного несколькими зарядами q₁, q₂, q₃, …?

Поместим в данную точку пробный заряд q. Пусть F₁ — это сила, с которой заряд q₁ действует на заряд q; F₂ — это сила, с которой заряд q₂ действует на заряд q и т.д. Из динамики вы знаете, что если на тело действует несколько сил, то результирующая сила равна геометрической сумме сил, т.е.

Разделим левую и правую часть уравнения на q :

Если учтем, что \(\dfrac{ \vec F}{q} = \vec E\), мы получим, так называемый, принцип суперпозиции полей

напряженность электрического поля, созданного несколькими зарядами q1, q2, q3, …, в некоторой точке пространства равна векторной сумме напряженностей \(\vec E_1 , \, \vec E_2 , \, \vec E_3\), … полей, создаваемых каждым из этих зарядов:

Благодаря принципу суперпозиции для нахождения напряженности поля системы точечных зарядов в любой точке достаточно знать выражение для напряженности поля точечного заряда. На рисунке 4, а, б показано, как геометрически определяется напряженность \(~\vec E\) поля, созданного двумя зарядами.

Для определения напряженности поля, создаваемого заряженным телом конечных размеров (не точечных зарядов), нужно поступать следующим образом. Мысленно разделить тело на маленькие элементы, каждый из которых можно считать точечным. Определить заряды всех этих элементов и найти напряженности полей, созданных всеми ими в заданной точке. После этого сложить геометрически напряженности от всех элементов тела и найти результирующую напряженность поля. Для тел сложной формы это трудная, но в принципе разрешимая задача. Для ее решения нужно знать, как заряд распределен на теле.

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – ​\( \varphi \)​, единица измерения в СИ – вольт (В).

Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

Обозначение – ​\( \Delta\varphi \)​, единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой ​\( U \)​ и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:. Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки

Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда ​\( q \)​ в точке, удаленной от него на расстояние ​\( r \)​, вычисляется по формуле:

Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (​\( r =R \)​, где ​\( R \)​ – радиус шара). Напряженность поля внутри шара равна нулю. Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

• Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
• Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

Разность потенциалов и напряженность связаны формулой:

Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

• установить характер и особенности электростатических взаимодействий объектов системы;
• ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
• записать законы сохранения и движения для объектов;
• выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
• составить систему уравнений и решить ее относительно искомой величины;
• проверить решение.

Примеры решения задач

Пример

Задание. Каков модуль вектора напряженности электрического поля
$\bar{E}$ в точке, которая определена радиус- вектором
$\bar{r}_{2}=7 \bar{i}+3 \bar{j}$ (в метрах), если электрическое поле создает положительный точечный
заряд (q=1Кл), который лежит в плоскости XOY и его положение задает радиус вектор
$\bar{r}_{1}=\bar{i}-5 \bar{j}$, (в метрах)?

Решение. Модуль напряжения электростатического поля, которое создает точечный заряд, определяется формулой:

$$E=\frac{1}{4 \pi \varepsilon \varepsilon_{0}} \frac{q}{r^{2}}(1.1)$$

r- расстояние от заряда, создающего поле до точки в которой ищем поле.

$$\bar{r}=\bar{r}_{2}-\bar{r}_{1}=6 \bar{i}-8 \bar{j}(1.2)$$

Из формулы (1.2) следует, что модуль $\bar{r}$ равен:

$$r=|\bar{r}|=\sqrt{36+64}=10(\mathrm{~m})$$

Подставим в (1.1) исходные данные и полученное расстояние r, имеем:

$$E=9 \cdot 10^{9} \frac{1}{100}=9 \cdot 10^{7}\left(\frac{B}{m}\right)$$

Ответ. $E=9 \cdot 10^{7}\left(\frac{B}{m}\right)$

Слишком сложно?

Формула напряженности электрического поля не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Запишите выражение для напряженности поля в точке, которая определена радиус – вектором
$\bar{r}$, если поле создается зарядом, который распределен по объему V с плотностью
$\rho=\rho(r)$ .

Решение. Сделаем рисунок.

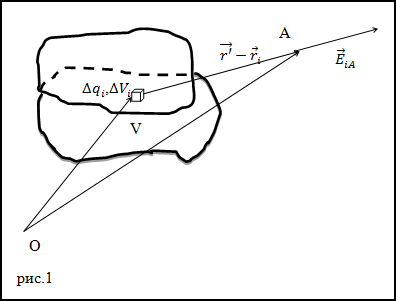
Проведем разбиение объема V на малые области с объемами
$\Delta V_{i}$ заряды этих объемов
$\Delta q_{i}$, тогда напряженность поля точечного заряда в точке А (рис.1) будет равна:

$$\bar{E}_{i A}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\Delta q_{i}}{\left|\bar{r}^{\prime}-\bar{r}_{i}\right|^{3}}\left(\bar{r}^{\prime}-\bar{r}_{i}\right)(2.1)$$

Для того чтобы найти поле, которое создает все тело в точке А, используем принцип суперпозиции:

$$\bar{E}_{A}=\sum_{i=1}^{N} \bar{E}_{i A}=\frac{1}{4 \pi \varepsilon_{0}} \sum_{i=1}^{N} \frac{\Delta q_{i}}{\left|\bar{r}^{\prime}-\bar{r}_{i}\right|^{3}}\left(\bar{r}^{\prime}-\bar{r}_{i}\right)(2.2)$$

где N – число элементарных объемов, на которые разбивается объем V.

Плотность распределения заряда можно выразить как:

$\rho\left(\bar{r}_{i}\right)=\frac{\Delta q_{i}}{\Delta V_{i}}(2.3)$

Из выражения (2.3) получим:

$\Delta q_{i}=\rho\left(\bar{r}_{i}\right) \Delta V_{i}(2.4)$

Подставим выражение для элементарного заряда в формулу (2.2), имеем:

$$\bar{E}_{A}=\frac{1}{4 \pi \varepsilon_{0}} \sum_{i=1}^{N} \frac{\rho\left(\bar{r}_{i}\right) \Delta V_{i}}{\left|\bar{r}^{\prime}-\bar{r}_{i}\right|^{3}}\left(\bar{r}^{\prime}-\bar{r}_{i}\right)(2.5)$$

Так ка распределение зарядов задано непрерывное, то если устремить
$\Delta V_i$ к нулю, то можно перейти от суммирования к интегрированию, тогда:

$$\bar{E}_{A}=\frac{1}{4 \pi \varepsilon_{0}} \int_{V} \frac{\rho(\bar{r})}{\left|\bar{r}^{\prime}-\bar{r}\right|^{3}}\left(\bar{r}^{\prime}-\bar{r}\right) d V$$

Ответ. $\bar{E}_{A}=\frac{1}{4 \pi \varepsilon_{0}} \int_{V} \frac{\rho(\bar{r})}{\left|\bar{r}^{\prime}-\bar{r}\right|^{3}}\left(\bar{r}^{\prime}-\bar{r}\right) d V$

Читать дальше: Формула пути.

Потенциал

Это еще одна характеристика электрического поля. Потенциал является накопленной энергией, которую явление может использовать для перемещения зарядов. Когда тот начинает двигаться, на это тратится вот этот самый ресурс, и в конечном итоге он становится равным нулю. Накапливается он обратным образом. В качестве примера можно взять все тот же заряд, но расположенный вне электрического поля. Как только некая сила перемещает его внутрь и двигает там, появляется потенциал.

Проще всего это представить на примере обычной пружины. В своем спокойном положении она не имеет никакого потенциала и просто представляет собой изогнутый кусок металла. Но как только мы начнем сдавливать ее, начнет возникать потенциал. Если отпустить пружину, она моментально распрямится и при этом подвинет все предметы, которые сможет, расположенные на ее пути. Если вернуться к рассматриваемым электрическим полям, то в их случае потенциал будет строго соответствовать приложенным усилиям на перемещение заряда. В современной науке этот показатель измеряется вольтами.

Напряжённость поля

Взаимодействие между заряженными телами описывается количественной характеристикой, определяющей структуру материи. Эта величина называется напряжённостью и определяется из отношения E = F / q, где F — сила, а q — заряд, помещённый в поле. Для однородной изотропной среды выражение можно получить, используя закон Кулона: E = (1 / 4 pE) * (q * r / er 2 r), где r — радиус-вектор.

Линии распространения напряжённости поля одинокого заряда во всех точках имеют радиальный вид. Кривые лежат от частицы при q > 0, к телу при q < 0. Для нескольких же носителей вводится понятие — пробный заряд. Он представляет собой результирующую напряжённость, определяемую суммой векторов сил, разделённых на значение введённой характеристики. Такой подход определения называется принципом суперпозиции.

Используя его, можно определить напряжённость как для системы одиночных носителей, так и проводника в целом. В последнем случае происходит непрерывное перераспределение. Именно поэтому заряженное тело можно представить как совокупность элементарных частиц dq.

Изображать непрерывными линиями напряжённости невидимое поле было предложено Майклом Фарадеем. С их помощью стало возможным определить количественное значение действующей силы. Показывают её с помощью изменения плотности, которую выбирают пропорционально векторам напряжённости по модулю. Другими словами, определяют число кривых, пронизывающих единичную площадь перпендикулярно к поверхности.

Поток вектора напряжённости можно вычислить по формуле: F = E * S * cos (a). Для неоднородного поля выражение проекции находят как произведение вектора площади на энергию материи: dF = E * dS. И в первом, и во втором случае поток считается скалярной величиной. Когда же рассматриваемая поверхность криволинейная, то площадь разбивается на простые контуры. В этом случае поток находится как сумма пронизывающих линий через элементарные поверхности. В любом случае поток, являясь алгебраической величиной, зависит от конфигурации поля и направления.

Изображение напряжённости даёт возможность получить полную картину, которая наглядно показывает, чему равна напряжённость в каждой точке поля и как она изменяется

Какой густоты рисовать линии — неважно.

Понятие напряженности.

В опыте

() мы встретились с величиной , с которой
также знакомы по школьному курсу физики. Настала пора уточнить, что это такое.

Пусть в пространстве имеется некоторое расположение зарядов (рис.4.1). Нас интересует,
как они будут действовать на пробный заряд q. По принципу суперпозиции

Поделим на величину пробного заряда.

Выражение справа зависит только от исходного расположения зарядов и от положения рассматриваемой точки.

Здесь нам необходима определенная осторожность. Если мы введем пробный заряд,
то исходные заряды могут прийти в движение, и изменить напряженность

Предел
q0 также не очень хорош, так как существует минимальный
заряд |e|. Поэтому лучше исходить из следующего положения:

В этом случае трудности снимаются, и нет необходимости упоминать о пробном заряде и о неподвижности.

§ 41. Линии напряженности электрического поля

Вектор напряженности электрического поля меняется от точки к точке (см. рис. 47, в). Если для каждой точки поля провести вектор напряженности, то эти векторы накладывались бы друг на друга и не дали бы наглядной картины распределения напряженности в поле. Поэтому английский ученый Фарадей для наглядного изображения действия сил в электрическом поле предложил графически электрическое поле изображать не векторами напряженности, а линиями напряженности.

Рис. 49. Линии напряженности электрического поля

Допустим, что в точках C₁, C₂, С₃ электрического поля точечных зарядов А и В (рис. 49, а) внесены пробные заряды q. В точке C₁ напряженность электрического поля, создаваемого зарядом А, будет Е_а, а создаваемого зарядом В — Е_в. По правилу параллелограмма результирующая напряженность в этой точке равна Е₁, а для точек С₂ и С₃ — соответственно Е₂ и Е₃. Оказывается, через точки C₁, C₂, С₃ и т д. (рис. 49, б) можно провести такую линию, что на ней напряженности поля в любой точке будут совпадать с касательными, проведенными к данной линии в этих точках. Линия, проведенная в электрическом поле так, что в любой ее точке касательная совпадает с вектором напряженности поля в этой точке, называется линией напряженности электрического поля.

Рис. 50. Линии напряженности точечных зарядов

Расположение наэлектризованных тел по линиям напряженности можно наблюдать на таком опыте. Наэлектризуем металлические диски, к которым прикреплены длинные полоски бумаги. Наэлектризуясь, последние располагаются в электрическом поле так, как действуют электрические силы, показывая тем самым форму линий напряженности. На рис. 50 изображены линии напряженности неоднородных электрических полей: линии напряженности отдельных точечных зарядов (рис. 50, а); электрического поля, образованного двумя разноименными зарядами (рис. 50, б) и одноименными (рис. 50, в).

Рис. 51. Однородное электрическое поле

Имеются две разноименно заряженные, равные, параллельно расположенные металлические пластинки (рис. 51). Если между ними в разные точки поля помещать одно и то же положительно заряженное точечное тело, то, удаляясь от одной пластинки, оно приблизится к другой (точки А и В). Электрические поля пластинок начнут действовать на заряженное тело по одной прямой и в одну сторону, поэтому общая сила, а значит и напряженность в любой точке поля, будут постоянными. Между пластинками электрическое поле однородное. Форму линий напряженности показывают листочки бумаги, прикрепленные к пластинкам. Линии напряженности однородного поля — параллельные прямые. Их считают направленными так, как направлен вектор напряженности. Началом и концом линий напряженности являются электрически заряженные тела, причем их началом считают заряды на поверхности положительно заряженного тела, а концом — заряды на поверхности отрицательно заряженного тела.

Рис. 52 Линии напряженности перпендикулярны к поверхности проводника

В каждой точке электрического поля напряженность имеет определенную величину и направление. В данной точке поля вектор напряженности является касательной к линии напряженности. Если через эту точку провести еще одну линию напряженности, то к ней уже вектор напряженности не будет касательным. Поэтому через каждую точку поля можно провести только одну линию напряженности. Отсюда следует, что линии напряженности нигде не пересекаются и не прерываются. Они являются незамкнутыми линиями: началом их считается положительно заряженное тело, а концом — отрицательно заряженное. Линии напряженности перпендикулярны к поверхности проводника. Если бы это было не так, то сила F, действующая на заряд наклонно к поверхности, разлагалась бы на две составляющие: F₁ и F₂ (рис. 52, а). Сила F₂, направленная вдоль поверхности, привела бы заряды в движение по поверхности, и не было бы наблюдаемого их равновесия.

Чтобы картина линий напряженности давала не только представление о направлении напряженности поля, но и показывала ее величину, условились через единицу площади S, расположенную перпендикулярно к вектору напряженности в этом месте поля, проводить столько N линий напряженности, скольким единицам равна напряженность Е в этой точке поля (рис. 52, б). Линии напряженности представляют собой лишь удобный способ графического изображения полей, в действительности этих линий в электрическом поле нет.

Определение

Электрическое поле неразрывно связано с магнитным полем, и возникает в результате его изменения. Эти два вида материи являются компонентами электромагнитных полей, заполняющих пространство вокруг заряженных частиц или заряженных тел.

Таким образом, данный термин означает особый вид материи, обладающий собственной энергией, являющийся составным компонентом векторного электромагнитного поля. У электрического поля нет границ, однако его силовое воздействие стремится к нулю, при удалении от источника – заряженного тела или точечных зарядов [].

Важным свойством полевой формы материи является способность электрического поля поддерживать упорядоченное перемещение носителей зарядов.

Рис. 1. Определение понятия «электрическое поле»

Энергия электрического поля подчиняется действию закона сохранения. Её можно преобразовать в другие виды или направить на выполнение работы.

Силовой характеристикой полей выступает их напряжённость – векторная величина, численное значение которой определяется как отношение силы, действующей на пробный положительный заряд, к величине этого заряда.

Характерные физические свойства:

• реагирует на присутствие заряженных частиц;
• взаимодействует с магнитными полями;
• является движущей силой по перемещению зарядов – как положительных ионов, таки отрицательных зарядов в металлических проводниках;
• поддаётся определению только по результатам наблюдения за проявлением действия.

Оно всегда окружает неподвижные статичные (не меняющиеся со временем) заряды, поэтому получило название – электростатическое. Опыты подтверждают, что в электростатическом поле действуют такие же силы, как и в электрическом.

Электростатическое взаимодействие поля на заряженные тела можно наблюдать при поднесении наэлектризованной эбонитовой палочки к мелким предметам. В зависимости от полярности наэлектризованных частиц, они будут либо притягиваться, либо отталкиваться от палочки.

Сильные электростатические поля образуются вблизи мощных электрических разрядов. На поверхности проводника, оказавшегося в зоне действия разряда, происходит перераспределение зарядов.

Вследствие распределения зарядов проводник становится заряженным, что является признаком влияния электрического поля.

Воздействие электрического поля на жизнь и здоровье человека

Электрическое поле волны низкой частоты, которые образуют заряд на теле человека и остаются на довольно неглубоком расстоянии от его поверхности. Протекающие в человеческом теле токи могут изменить направление своего движения под воздействием полей с переменным электротоком. Именно по этой причине некоторые люди чувствуют «шевеление» волос, когда находятся на территории воздушных линий электропередач переменного тока.

Электрическое поле может нанести человеку непоправимый вред. Как правило, негативное воздействие электричества происходит, когда люди регулярно пользуются мобильными телефонами.

Ещё один пример возможного наблюдения электрического поля в повседневной жизни – его возникновение вблизи дисплеев телевизоров с кинескопом. Если поднести руку к экрану такого телеприёмника, волоски на ней словно «вздыбятся». Это явление происходит именно из-за воздействия электрического поля.

Еще рекомендую посмотреть лекцию профессора на тему “Электрическое поле”:

https://youtube.com/watch?v=JOY70VjjdkU

Проводники в электрическом поле

Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.

Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.

Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.

Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.

Важно!Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей. На этом основана электростатическая защита

На этом основана электростатическая защита.

Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.

Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.

Важно! Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны)

Куда направлен вектор Е

Обратим в очередной раз внимание на формулу:

\

Заряд q – скалярная величина. А сила F – векторная.

Воспользуемся математическими свойствами векторов: разделив вектор F на скаляр q, мы получим новый вектор E:

1. его длина отличается от вектора F.
2. направления векторов F и E совпадают (либо векторы F и E направлены в противоположные стороны).

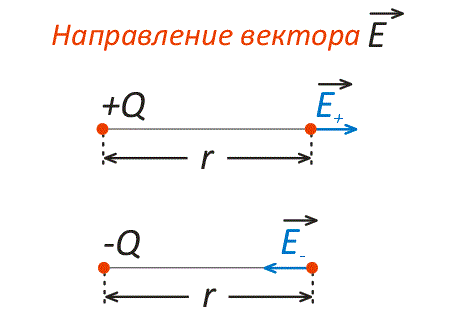Рис. 8. Направление вектора E выбирается от положительных зарядов и в сторону отрицательных зарядов

Примечание: Однонаправленные или противоположно направленные, то есть, параллельные векторы, называют коллинеарными. У них может отличаться длина.

Будет ли поле действовать на заряд, расположенный между силовыми линиями

У начинающих изучать электростатику часто возникает вопрос, а будет ли на заряд, находящийся на рисунке между силовыми линиями, действовать сила с стороны электрического поля? Конечно, будет.

Не имеет значения, находится ли заряд на силовой линии на рисунке, или в пространстве между силовыми линиями. Поле существует во всех точках рассматриваемой области, поэтому на заряд будет действовать сила в любой точке поля, независимо, находится ли эта точка на силовой линии, или нет.

Примечание: Силовые линии – это всего лишь способ графического обозначения поля в некоторой области пространства. Поле существует во всех точках пространства, а не только на силовых линиях.

Похожие записи:

Калибровка датчика приближения xiaomi: что это такое и как настроить модуль? Какую лампочку выбрать для дома? сравним led, люминесцентные и лампы накаливания Назначение и принцип действия измерительных трансформаторов Параметры расчетной схемы Активный сабвуфер! чертежи, схема, инструкция! Виды выключателей света для использования в квартире или доме: описание и характеристики