Применение
Использование такой схемотехники на практике демонстрируют следующие примеры. Для расчетов электрических параметров без учета сопротивления нагрузки подойдут рассмотренные выше ручные и автоматизированные методики.
Потенциометры
Если резистор оснастить ползунком и соответствующим приводом, сопротивления можно будет менять плавно. Это решение позволяет точнее менять напряжения на выходе, по сравнению с дискретными схемами. Главный недостаток – усложнение конструкции, что, кроме удорожания, снижает надежность. Приходится обеспечивать герметичность рабочей зоны для исключения загрязнения и предотвращения коррозийных процессов.
Принципиальная схема потенциометра
Резистивные датчики
В этом варианте пользуются способностью некоторых материалов увеличивать/ уменьшать электрическое сопротивление под воздействием температуры, светового потока, других внешних воздействий. Созданный на основе этих принципов датчик устанавливают в плечо делителя. По уровню напряжения на выходе контролируют изменение соответствующих параметров.
Цепи обратной связи в усилителях
Таким решением обеспечивают необходимый коэффициент усиления. На представленной ниже схеме этот параметр не будет никогда ниже единицы. Для повышения уровня преобразования увеличивают значение сопротивления R2 по отношению к R1.
Делитель напряжения в цепи обратной связи
Простейшие электрические фильтры
Для фильтрации заменяют конденсатором резисторы R1 или R2. В первом варианте устройство беспрепятственно пропускает высокочастотные составляющие. При снижении частоты до определенного уровня реактивное сопротивление увеличивается, препятствует прохождению тока. Аналогичным образом делают изменения в нижнем плече делителя с целью отсечения низких частот.
Усилитель напряжения
Переменным резистором изменяют уровень сигнала для получения необходимой громкости звучания. В таких устройствах применяют элементы с логарифмической характеристикой изменения сопротивления, что хорошо соответствует естественному механизму восприятия человеческими органами слуха.
Параметрический стабилизатор напряжения
В таких схемах нижнее плечо делителя можно создать с применением стабилитрона. Его вольтамперные характеристики выбирают таким образом, чтобы выходное напряжение сохраняло нужное значение при изменении входных параметров.
Ограничения в применении
Из приведенных в таблице примеров расчетов хорошо видно, как значительно увеличиваются потери при уменьшении сопротивления цепи. Энергия расходуется впустую для нагрева окружающей среды. При большой мощности рассеивания приходится использовать принудительные системы охлаждения, пассивные радиаторы.
В приведенных расчетах не учитывалась нагрузка. Если добавить соответствующее реальным условиям сопротивление, образуются дополнительные потери в параллельной цепи.
Влияние сопротивления нагрузки
На первой части рисунка изображен типовой делитель, обеспечивающий выходное напряжение 5 V. При потреблении тока 0,01 А сопротивление нагрузки составит 0,5 кОм. Пользуясь формулой расчета для параллельной цепи, несложно выяснить суммарное значение R = 1/(1/R2 + 1/Rнагрузки) = 0,25 кОм. Это добавление уменьшит плановое значение Uвых до 3,46 V.
Уменьшением R2 можно снизить вредное влияние на выходное напряжение (4,75 V). Однако такой способ, приведенный на второй части рисунка, сопровождается значительными потерями энергии. Ток будет проходить по участку с меньшим сопротивлением, не выполняя полезные функции. В данном примере необходимо выбрать R1, рассчитанный на мощность не менее 2 Вт, чтобы обеспечить надежную работу устройства.
Как работает делитель напряжения
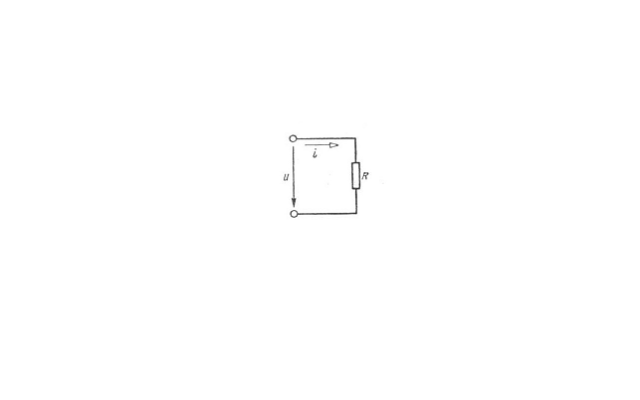
Делитель напряжения это устройство, осуществляющее регулировку выходного напряжения по отношению значения входного напряжения, в соответствии с коэффициентом передачи. То есть, из большего значения получается меньшее, а само напряжение бывает постоянным или переменным. Самая простая схема делителя напряжения состоит как минимум из двух сопротивлений. Если их сопротивления равны между собой, то и падения напряжения будут одинаковыми. Поэтому, по закону Ома напряжение на выходе прибора будет ровно в два раза ниже, чем на входе. В других случаях для расчетов падения напряжений используются формулы.
Основной функцией делителя напряжения в электрических цепях является снижение напряжения и получение нескольких его значений с фиксированными показателями на различных участках. Его основой служат резисторы или реактивные сопротивления в количестве два и более элементов.
Простейший делитель представляется в виде двух участков цепи, называемых плечами. Верхним плечом считается участок между нулевой точкой и положительным напряжением, а нижним – участок между нулевой точкой и минусом. После того как определены исходные данные, можно сделать самый простой расчет делителя напряжения.
В качестве примера рассматриваются два резистора, соединенные последовательно. К ним подается напряжение U, которое может быть переменными или постоянным. После этого в действие вступает закон Ома, когда при последовательном соединении резисторов, общее сопротивление составит сумму их номиналов. В виде формы это будет выглядеть следующим образом: I = U/Rобщ, в которой Rобщ = R1+R2. Следовательно, I = U/(R1+R2).
Сила тока при последовательно соединенных резисторов, будет одинаковой на всех участках цепи. Если у каждого резистора имеется собственное значение сопротивления, то по закону Ома у них образуются совершенно разные напряжения. Сопротивлению R1 соответствует напряжение U1, а сопротивлению R2 – напряжение U2. В результате получается следующая ситуация, выраженная формулой I = U2/R2 = U1/R1 = U/(R1+R2).
Для того, чтобы найти значения напряжений U1 и U2, необходимо выполнить такие действия: U1 = U x R1/(R1+R2) и U2 = U x R2/(R1+R2). Если правые части каждого уравнения сложить друг с другом, то в результате получится значение входящего напряжения U, состоящее из суммы напряжений U1 и U2, то есть U = U1 + U2. Это значит, что сумма падений напряжений на всех последовательно соединенных резисторах, будет равна напряжению источника питания, то есть входящему напряжению. Таким образом, данное выражение есть ни что иное, как формула делителя напряжения. Практически получается, что входящее напряжение U оказалось разделенным на два напряжения с собственными значениями – U1 и U2.
Во многих случаях необходимо, чтобы процесс разделения напряжения осуществлялся плавно. С этой целью был изобретен прибор – переменный резистор. Работа устройства происходит по установленной схеме. Два крайних контакта обладают постоянным сопротивлением, а сопротивление среднего контакта относительно крайних контактов будет изменяться в зависимости от направления вращения регулятора. С помощью переменных резисторов добавляется громкость в звуковых колонках, у радиоприемников и телевизоров старых марок.
Как понизить напряжение с помощью резистора
Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость снизить входное напряжение. Проще всего этого можно добиться, используя схему с двумя резисторами, более известную как делитель напряжения. Классическая схема выглядит так:
В этом случае напряжение подаётся на два резистора с использованием параллельного подключени, а на выходе его получают с одного. Подбор номиналов резисторов осуществляют по формуле так, чтобы напряжение, снимаемое на выходе, составляло какую-то часть от подаваемого. Расчет резистора для понижения напряжения можно воспользовавшись формулой, основанной на законе Ома:
Uвых= (Uвх*R2)/(R1+R2), где
Uвх – напряжение на входе, В;
Uвых – напряжение на выходе, В
R1 – показатель сопр. 1-ого резистора (Ом)
R2 – показатель сопр. 2-ого элемента, (Ом)
Подбор резистора для понижения напряжения
Для подбора нужного сопротивления резистора можно воспользоваться готовыми онлайн-калькуляторами или программами для моделирования работы электронных схем. Симуляторы электрических цепей способны не только рассчитать напряжение на выходе в зависимости от сопротивления элементов и способа их подключения, но и обладают функционалом, позволяющим визуализировать то, как падает ток и напряжение на резисторе. Например, приложение EveryCircuit позволяет изменять в схеме параметры элементов, выбирать скорость симуляции, получать данные в различных точках. При этом можно наблюдать за динамикой изменения значений, используя для ввода входных параметров вращающийся лимб в нижнем правом углу.
Существует ещё ряд бесплатных программ для эмуляции, позволяющие выполнить, в том числе, расчёт резистора при понижении напряжения, например:
- EasyEDA;
- Circuit Sims;
- DcAcLab;
и другие.
В статье мы ознакомились с понятием сопротивления, узнали о его единицах измерения, о маркировке резисторов, о программах эмулирующих работу цепи и облегчающих подбор нужного сопротивления, а также рассмотрели примеры расчёта падения напряжения на резисторе.
Расчет гасящего конденсатора для светодиода
Разберем подробный расчет, ниже сможете найти форму онлайн калькулятора.
Расчет емкости конденсатора для светодиода:
С(мкФ) = 3200 * Iсд) / √(Uвх² — Uвых²)
С мкФ – ёмкость конде-ра. Он должен быть рассчитан на 400-500В; Iсд – номинальный ток диода (смотрим в паспортных данных); Uвх – амплитудное напряжение сети — 320В; Uвых – номинальное напряжение питания LED.
Можно встретить еще такую формулу:
C = (4,45 * I) / (U — Uд)
Она используется для маломощных нагрузок до 100 мА и до 5В.
Подключение одного светодиода
Для расчета емкости конде-ра нам понадобится:
- Максимальный ток диода – 0,15А;
- напряжение питания диода – 3,5В;
- амплитудное напряжение сети — 320В.
Для таких условий параметры конде-ра: 1,5мкФ, 400В.
Подключение нескольких светодиодов
При расчете конденсатора для светодиодной лампы необходимо учитывать, что диоды в ней соединены группами.
- Напряжение питания для последовательной цепочки – Uсд * количество LED в цепи;
- сила тока – Iсд * количество параллельных цепочек.
Для примера возьмём модель с шестью параллельными линиями из четырёх последовательных диодов.
Напряжение питания – 4 * 3,5В = 14В; Сила тока цепи – 0,15А * 6 = 0,9А;
Для этой схемы параметры конде-ра: 9мкФ, 400В.
Калькулятор для расчета делителя напряжения
Делитель напряжения — это простой и удобный способ получить нужное напряжение в определенной точке схемы. Он используется в цепях обратной связи для измерения выходных параметров, когда на выходе десятки вольт, а измерительный вход микросхемы рассчитан на единицы или доли вольт и во множестве других целей. Простейший вариант строится на резисторах их может быть 2 и больше.
Давайте разберемся как рассчитать данный элемент цепи. Можно сделать это вручную или использовать следующий онлайн калькулятор, который выполняет расчет делителя напряжения на резисторах:
Главное, что нельзя забывать, так это то, что ток делителя должен быть на 1 и более порядков выше, чем входной ток нагрузки. Это нужно, чтобы минимизировать просадки напряжения и сохранить стабильность выходных параметров. После этого приступайте к расчетам по току и напряжению.
Если ваш делитель состоит из двух элементов, то ток через него рассчитывают по формуле:
I=Uвх/(R1+R2)=Uвх/Rобщ
Или сопротивление по заданному току:
Rобщ=Uвх/I
Нам известно R общее при заданном I, входное напряжение и сколько нам нужно получить на выходе. Рассчитываем сопротивления:
R2=Uвых*Rобщ/Uвх
Тогда:
R1=Rобщ-R2
Если нужно определить параметры цепочки по известным сопротивлениям и входному напряжению — рассчитывают выходное по формуле:
Uвых=Uвх*R2/R1+R2
Значит, зная напряжение на выходе можно рассчитать его и на входе:
Uвх=(Uвых*R1+R2)/R2
Это основной метод расчета резистивного делителя, бывает еще и емкостной или индуктивный. В этом случае вместо сопротивления активного R в расчетах фигурирует сопротивление реактивное Xc или Xl.
Для регулировки выходного напряжения резисторного делителя вместо нижнего сопротивления устанавливают подстроечный или переменный резистор. Расчеты при этом ничем не отличаются — в них используют максимальное значение на переменном резисторе. Также можно ограничить минимальное выходное напряжение, установив последовательно с переменным постоянное, тогда минимальное рассчитывается без учета переменника. Такую схему удобно использовать, если у вас резисторы с большим допуском, а нужно получить точные выходные параметры.
Вы можете сэкономить время, воспользовавшись онлайн калькулятором, в нем вы можете рассчитать номиналы элементов с учетом нужных выходного и входного напряжения. Использование калькулятора сэкономит ваше время, если нужно посчитать большую схему или вы запутались и не можете разобраться, как посчитать резистивный делитель с нагрузкой.
Учтите, что элементы нужно подбирать не только по номиналу, но и по мощности, потому что при большом токе потребления нагрузки, нужно рассчитывать схему на большие токи. В результатах расчетов онлайн калькулятора будет указано, на сколько ватт нужен резистор.
Опубликовано: 15.08.2018 Обновлено:15.08.2018 нет комментариев
Примеры применения делителя тока
- Как делитель тока. Представьте, что у Вас есть светодиод, номинальный ток через который 17 мА (миллиампер) и есть схема, через которую протекает ток 30 мА. При маленьком токе светодиод будет гореть тускло, при большем — выйдет из строя. Для того, чтобы светодиод работала в номинальном режиме (ток 17 мА) необходимо ток 30 мА разделить на 17 и 13 миллиампер. Данную задачу выполняют простейшие делители тока на резисторах.
- Датчик параметр — ток. Сопротивление резистивных элементов зависит от многих параметров, например растяжение и сжатие. Начинаем выполнять механические воздействия над одним из сопротивлений. В результате изменяется его сопротивление. Согласно закону Ома ток через это сопротивление будет изменяться. Согласно первому закону Кирхгофа общий ток так же будет изменяться.
- Измерение больших токов. Через первое сопротивление пропускается почти весь ток, через второй малая часть (миллиамперы или микроамперы). Измерение производится миллиамперов.
Формула для расчета делителя напряжения
Начинающие радиолюбители часто задаются главным вопросом, как правильно рассчитать напряжение после резистора. Для этого необходимо знать, какой ток пойдет по цепи. В простейших схемах постоянного тока его вычисляют по линейному закону Ома. Формула расчета выглядит U=I*R, где:
- U — напряжение, В;
- I — ток, А;
В цепях с синусоидальным током, где присутствует реактивное сопротивление катушки или конденсатора, формула выглядит как R=1/(2*pi*f*L) и R=1/(2*pi*f*C) соответственно. В формуле использованы показатели:
График зависимости показателей от сопротивления
- R — реактивное сопротивление;
- R — сопротивление, Ом.
- pi — постоянное число Пи, равное 3,14;
- f — частота, Гц;
- L — индуктивность катушки, Генри;
- C — емкость конденсатора, Фарад.
Получив в расчетах внутреннюю резистивность элементов, далее можно воспользоваться линейной формулой для вычисления выходного значения.
На резисторе
В схеме делителя всегда участвует не меньше двух узлов нагрузки. Их коэффициенты могут быть равны другу, но и отличаться. Поэтому порой возникает необходимость получить номинал выходного вольтажа для каждого из них. Для этого используют всем известную формулу закона Ома: U=I*R.
Вам это будет интересно Все об скважности сигнала
После резистора
Для расчета показателя после резистора необходимо учитывать номиналы обоих элементов, так как они работают совместно друг с другом. Применив закон Ома, получается следующая формула: Uвых=Uпит*R1/(R1+R2), где:
- Uвых — вольтаж на выходе, В;
- Uпит — входной вольтаж, В;
- R1 — первый узел, Ом;
- R2 — второй узел, Ом.
Падение потенциалов за резистором рассчитывают для каждого узла в отдельности. То есть для второго элемента формула будет выглядеть так: Uвых=Uпит*R2/(R1+R2).
Делитель позволяет разработчикам получить несколько номинальных значений выходного напряжения от одного питающего источника. По этой причине схема получила широкое применение в электронике как в понижающих блоках питания, так и в качестве интегрированного узла электроцепи.
Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях
Делитель на резисторах — отличается своей универсальностью: используют при постоянном и переменном токе, но только при пониженном сопротивлении цепи.
Тогда на каждом из резисторов: U1= I х R1 и U2 = I х R2 Ток в цепи устройства:
Уменьшение на конденсаторах применяют для цепей с высоким переменным током. В нём минимальная потеря энергии на выходе. Реактивное сопротивление конденсатора зависит от его электроёмкости и частоты напряжения в цепи.
Формула для вычисления сопротивления:
Делитель на индуктивностях используется при переменном низком токе на высоких частотах. Сопротивление катушки переменного тока прямо пропорционально зависит от индуктивности и частоты. У провода катушки имеется активное сопротивление, из-за чего мощность такого прибора больше, чем у аналогов.
Сопротивление катушки находится по формуле:
Общий случай
Делитель напряжения относительно земли создается путем последовательного соединения двух электрических сопротивлений , как показано на рисунке 1. Входное напряжение прикладывается к последовательным импедансам Z 1 и Z 2, а выходное напряжение — это напряжение на Z 2 . Z 1 и Z 2 могут состоять из любой комбинации элементов, таких как резисторы , катушки индуктивности и конденсаторы .
Если ток в выходном проводе равен нулю, то соотношение между входным напряжением V in и выходным напряжением V out будет следующим:
- Vотытзнак равноZ2Z1+Z2⋅Vяп{\ displaystyle V _ {\ mathrm {out}} = {\ frac {Z_ {2}} {Z_ {1} + Z_ {2}}} \ cdot V _ {\ mathrm {in}}}
Доказательство (с использованием закона Ома ):
- Vяпзнак равноя⋅(Z1+Z2){\ Displaystyle V _ {\ mathrm {in}} = I \ cdot (Z_ {1} + Z_ {2})}
- Vотытзнак равноя⋅Z2{\ Displaystyle V _ {\ mathrm {out}} = I \ cdot Z_ {2}}
- язнак равноVяпZ1+Z2{\ displaystyle I = {\ frac {V _ {\ mathrm {in}}} {Z_ {1} + Z_ {2}}}}
- Vотытзнак равноVяп⋅Z2Z1+Z2{\ displaystyle V _ {\ mathrm {out}} = V _ {\ mathrm {in}} \ cdot {\ frac {Z_ {2}} {Z_ {1} + Z_ {2}}}}
Функция передачи (также известная как делитель отношение напряжения ) эта схема является:
- ЧАСзнак равноVотытVяпзнак равноZ2Z1+Z2{\ displaystyle H = {\ frac {V _ {\ mathrm {out}}} {V _ {\ mathrm {in}}}} = {\ frac {Z_ {2}} {Z_ {1} + Z_ {2}} }}
В целом эта передаточная функция представляет собой комплекс , рациональная функция от частоты .
Законы Кирхгофа
Первый закон
Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два. Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю. Если посмотреть на схему, I1 — это ток, который заходит в узел, I2 и I3 — это электроны, которые вытекают из него. Применяя формулировку первого закона можно записать формулу по-другому: I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.
Второй закон Кирхгофа
Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
Подключение нагрузки
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):
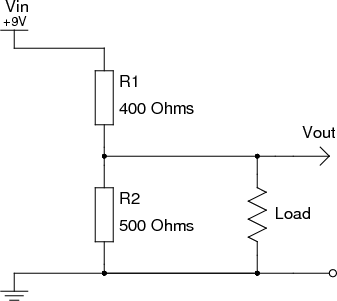
В этом случае Vout уже не может быть расчитано лишь на основе значений Vin, R1 и R2: сама нагрузка провоцирует дополнительное падение напряжения (voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда её сопротивление
В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:
Подставив значение в общую формулу расчёта Vout, получим:
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L. Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.
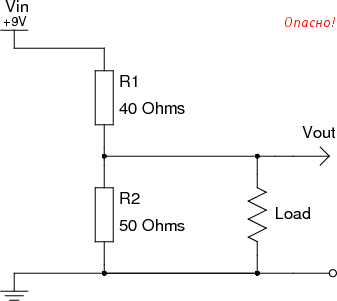
Пропорция сохраняется, Vout не меняется:
А потери уменьшатся:
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.
Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на R1 равна:
А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.
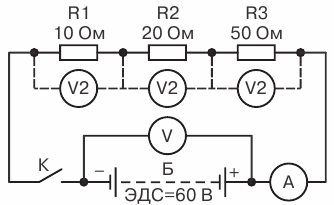
Параллельное и последовательное соединение резисторов, решение задач
Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно. Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. На схеме присутствует параллельная и последовательная часть соединения элементов
Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?
Будет интересно Что такое фоторезистор?
Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.
Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше. Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом
Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех. Заменяем эти сопротивление одним эквивалентным R23465
В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.
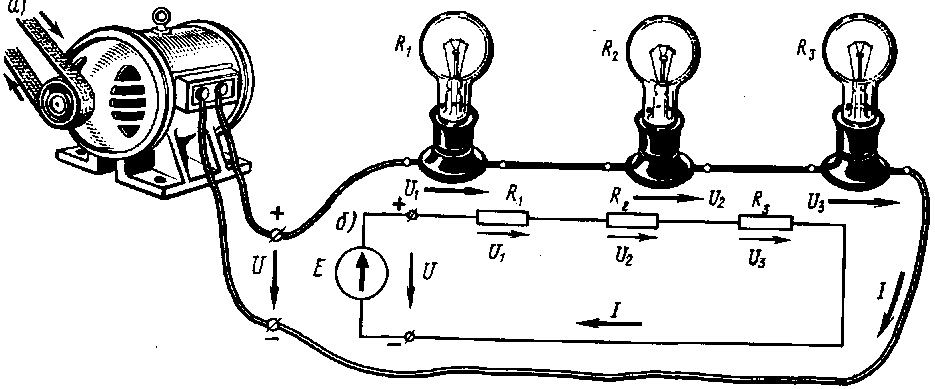
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.
Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно. На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Типы подключений.
Калькулятор делителя напряжения
Разделитель напряжения представляет собой схему, используемую для создания напряжения, которое меньше или равно входному напряжению.
Выходное напряжение (V out )
Вольт (V)
Как найти выходное напряжение цепи делителя
Два делителя напряжения резистора являются одной из наиболее распространенных и полезных схем, используемых инженерами. Основная цель этой схемы заключается в уменьшении входного напряжения до более низкого значения в зависимости от отношения двух резисторов. Этот калькулятор помогает определить выходное напряжение схемы делителя с учетом входного (или источника) напряжения и значений резисторов
Обратите внимание на то, что выходное напряжение в реальных схемах может быть различным, поскольку резистор и сопротивление нагрузки (при подключении выходного напряжения) становятся факторами
Уравнение
$$ V_ {out} = V_ {in} * \ frac {R_ {2}} {R_ {1} + R_ {2}} $$
Где:
$$ V_ {out} $$ = Выходное напряжение. Это уменьшенное напряжение.
$$ V_ {in} $$ = Входное напряжение.
$$ R_ {1} $$ и $$ R_ {2} $$ = значения резистора. Отношение $$ \ frac {R_ {2}} {R_ {1} + R_ {2}} $$ определяет масштабный коэффициент.
Приложения
Поскольку делители напряжения довольно распространены, их можно найти в ряде приложений. Ниже приведены лишь некоторые из мест, где эта схема найдена.
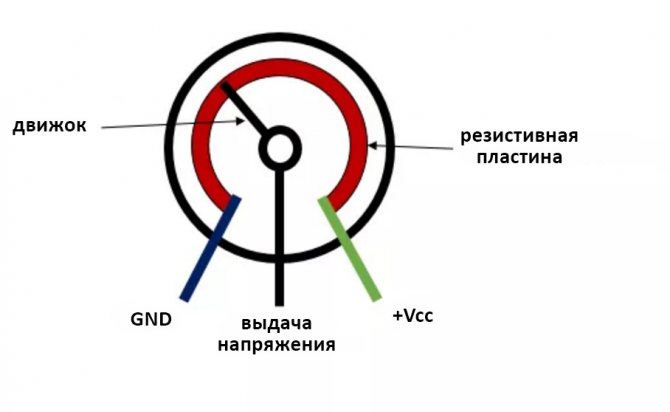
потенциометры
Возможно, наиболее распространенной схемой делителя напряжения является то, что используется потенциометр, который является переменным резистором. Схематическое изображение потенциометра показано ниже:
«Горшок» обычно имеет три внешних контакта: два являются концами резистора, а один подключен к рычагу стеклоочистителя. Стеклоочиститель разрезает резистор пополам и перемещает его, регулируя соотношение между верхней половиной и нижней половиной резистора. Соедините два внешних выводы к напряжению (вход) и ссылку (земля) со средним (стеклоочистители штифтом) в качестве выходного контакта и вы сам делитель напряжения.
Уровневые сдвиги
Другая область, в которой используются делители напряжения, — это когда напряжение должно быть выровнено. Наиболее распространенным сценарием является взаимодействие сигналов между датчиком и микроконтроллером с двумя разными уровнями напряжения. Большинство микроконтроллеров работают при напряжении 5 В, в то время как некоторые датчики могут принимать только максимальное напряжение 3, 3 В. Естественно, вы хотите выровнять напряжение от микроконтроллера, чтобы избежать повреждения датчика. Пример схемы показан ниже:
Схема выше показывает схему делителя напряжения, включающую резистор 2 кОм и 1 кОм. Если напряжение от микроконтроллера составляет 5 В, то пониженное напряжение на датчик рассчитывается как:
$$ V_ {out} = 5 * \ frac {2k \ Omega} {2k \ Omega + 1k \ Omega} = 3.33 V $$
Этот уровень напряжения теперь безопасен для работы датчика
Обратите внимание, что эта схема работает только для выравнивания напряжений и не выравнивания
Ниже приведены некоторые другие комбинации резисторов, используемые для выравнивания часто встречающихся напряжений:
| Комбинация резисторов | использование |
| 4, 7 кОм и 6, 8 кОм | От 12 В до 5 В |
| 4, 7 кОм и 3, 9 кОм | 9V до 5V |
| 3, 6 кОм и 9, 1 кОм | От 12 В до 3, 3 В |
| 3, 3 кОм и 5, 7 кОм | От 9 В до 3, 3 В |
Чтение резистивного датчика
Многие датчики являются резистивными устройствами и большинством микроконтроллеров считывают напряжение, а не сопротивление. Таким образом, резистивный датчик обычно подключается в цепи делителя напряжения с резистором для взаимодействия с микроконтроллером. Пример установки показан ниже:
Термистор — это датчик, сопротивление которого изменяется пропорционально температуре. Скажем, что термистор имеет сопротивление комнатной температуре 350 Ом. Сопряженное сопротивление выбирается равным 350 Ом.
Когда термистор находится при комнатной температуре, выходное напряжение:
$$ V_ {out} = 5 * \ frac {350 \ Omega} {350 \ Omega + 350 \ Omega} = 2.5V $$
Когда температура увеличивается, сопротивление термистора изменяется до 350, 03 Ом, выход изменяется на:
$$ V_ {out} = 5 * \ frac {350.03 \ Omega} {350 \ Omega + 350.03 \ Omega} = 2.636V $$
Такое небольшое изменение напряжения обнаруживается микроконтроллером. Если функция передачи термистора известна, теперь можно рассчитать эквивалентную температуру.
Дальнейшее чтение
Техническая статья — Разделители напряжения и тока: что это такое и что они делают
Учебник — Глава 6 — Цепи Divider и законы Кирхгофа
Учебник — Потенциометр в качестве делителя напряжения
Рабочий лист — Цепь делителя напряжения
Описание
Принцип действия делителей основан на методе емкостно-омического деления высокого напряжения.
Делители состоят из двух резистивно-емкостных сборок в диэлектрических корпусах, двух электростатических экранов и опоры.
Каждый модуль преобразователя представляет собой диэлектрический корпус с металлическими фланцами, в который помещены резистивно-емкостные сборки. Во фланцах предусмотрены отверстия для охлаждения резистивно-емкостных сборок. Нижняя резистивноемкостная сборка имеет отвод с высоковольтным вводом на напряжение 35/V3 кВ. В плече низкого напряжения преобразователя установлен разрядник для защиты от перенапряжений.
Делители выпускаются в следующих модификациях ДН-160пт/2 и ДН-160пт/2-БК. Модификация ДН-160пт/2-БК поставляется с блоком коррекции БК-1, модификация ДН-160пт/2 поставляется без блока коррекции БК-1.
Блок коррекции представляет собой электронный прибор в металлическом корпусе, на передней панели которого расположены органы управления и индикации, а на задней панели -разъем сетевого питания, входные клеммы для получения сигнала от преобразователя и выходные клеммы для передачи сигнала на входы низковольтных измерительных приборов.
Общий вид средства измерений представлен на рисунке 1.
Схема пломбировки от несанкционированного доступа и нанесения знака поверки представлена на рисунке 2.
Делитель напряжения составной ДН-160пт/2
Рисунок 1 — Общий вид средства измерений
Рисунок 2 — Схема пломбировки от несанкционированного доступа (А и Б).
Емкостной делитель напряжения
Простейший емкостной делитель напряжения состоит из двух последовательно соединенных конденсаторов и используется для снижения величины U на отдельных элементах электрической цепи.
Делитель постоянного напряжения на конденсаторах чаще всего применяют многоуровневых инверторов напряжения, широко используемых как на электроподвижном составе, так и в других направлениях силовой электроники.
Главная сложность практического применения такой схемы (и всех подобных схем) заключается в невозможности обеспечения равномерного разряда конденсаторов, вследствие чего напряжения на них будет распределяться не поровну. Чем сильнее разряжен один конденсатор по сравнению с другим (иди с другими), тем большая разница в U будет на них, что наглядно отображает формула:
По этой причине подобные схемы крайне нестабильно работают и обязательно предусматривают узлов подзарядки конденсаторов с целью выравнивания напряжения на последних.
Емкостной делитель напряжения в цепи переменного тока
В радиоэлектронике в большей степени находят применение емкостные делители переменного напряжения.
Конденсатор, как и катушка индуктивности, относится к реактивному элементу, то есть потребляет реактивную мощность от источника переменного тока, в отличие от резистора, который является активным элементов и потребляет исключительно активную мощность.
Реактивный элемент
Здесь следует кратко пояснить разницу между активной и реактивной мощностями. Активная мощность выполняет полезную работу и реализуется только в том случае, когда ток и напряжение направлены в одном направлении и не отстают друг от друга, то есть находятся в одной фазе, что имеет место только на резисторе. На конденсаторе ток отстает от напряжения на угол φ = 90°. В результате чего ток напряжение находятся в противофазе, поэтому когда ток имеет максимальное значение напряжение равно нулю, а произведение этих двух величин дают мощность, которая в таком случае равна нулю, так как один из множителей равен нулю. Следовательно, мощность не потребляется.
Аналогичные процессы протекают и в цепи с катушкой индуктивности. Разница лишь в том, что на индуктивности i отстает от u на угол φ = 90°.
Реактивная мощность проявляется только в цепях переменного тока. Она составляет часть полной мощности и определяется по формуле:
Реактивная мощность в отличие от активной, не потребляется нагрузкой, а циркулирует между источником питания и нагрузкой. Поэтому конденсатора и катушка индуктивности являются реактивными элементами, не потребляющими активную мощность и по этой причине они практически не нагреваются.
Расчет сопротивления делителя напряжения на конденсаторах заключается в определении необходимых значений сопротивлений.
Сопротивление конденсатора XC является величиной не постоянной и зависит от частоты переменного тока f и емкости C:
Как видно из формулы, сопротивление снижается с увеличением частоты и емкости. Для постоянного тока, частота которого равна нулю, сопротивление стремится к бесконечности, поэтому, рассматриваемая далее схема емкостного делителя напряжения не применяется постоянном токе.
Для снижения величины uвых, например в два раза, емкости C1 и C2 должны быть равны. Универсальные формулами для определения выходных uвых1 и uвых2 в зависимости от входного и емкостей C1 и C2 имеют вид, аналогичный для резисторных делителей:
Поскольку частота переменного тока для всех конденсаторов одинакова, то формулу можно упростить:
Индуктивный делитель напряжения
В качестве делителей переменного напряжения также, но гораздо реже, применяют катушки индуктивности, которые относятся к реактивным элементам. Однако, в отличие от конденсаторов, которые являются накопителями электрического поля, катушки индуктивности накапливают магнитное поле.
Индуктивное сопротивление зависит от индуктивности L и частоты переменного тока f. С ростом этих параметров сопротивление катушки переменному току возрастает.
XL = 2πfL.
Упрощенный вариант формулы:
https://youtube.com/watch?v=wNwYNlvFsi8
Как вы наверняка уже заметили, чтобы рассчитать емкостной делитель напряжения достаточно знать емкости конденсаторов, а индуктивный делитель – индуктивности.
- Делитель напряжения на резисторах
- Инвертор напряжения
- Умножитель напряжения
- Замена электролитического конденсатора