Виды пассивных элементов
Внутреннее сопротивление — формула
Данные устройства характеризуются тем, что вместо рассеивания энергии склонны к ее накоплению. Разные типы таких деталей создают различные формы сопротивления.
Катушка индуктивности
Это радиокомпонент, представляющий собой проводниковый элемент спиральной или винтообразной формы, покрытый изоляцией. В схемах катушки используют для нивелирования помех и искажений, снижения величины переменного тока, генерации магнитного поля. Длинные тонкие элементы носят название соленоидов. Катушки отличаются небольшими величинами активной сопротивляемости и емкости, но обладают индуктивностью, генерируя электродвижущую силу.
Подключение катушки в электрическую цепь
Емкостной элемент
Примером этого вида деталей является конденсатор. Он включает в себя две проводящие обкладки, между которыми находится диэлектрический материал. Протекание электротока обусловлено накоплением и отдачей обкладками своего заряда.
Подсоединение конденсатора в электроцепь
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
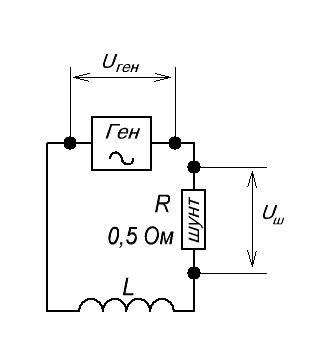
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
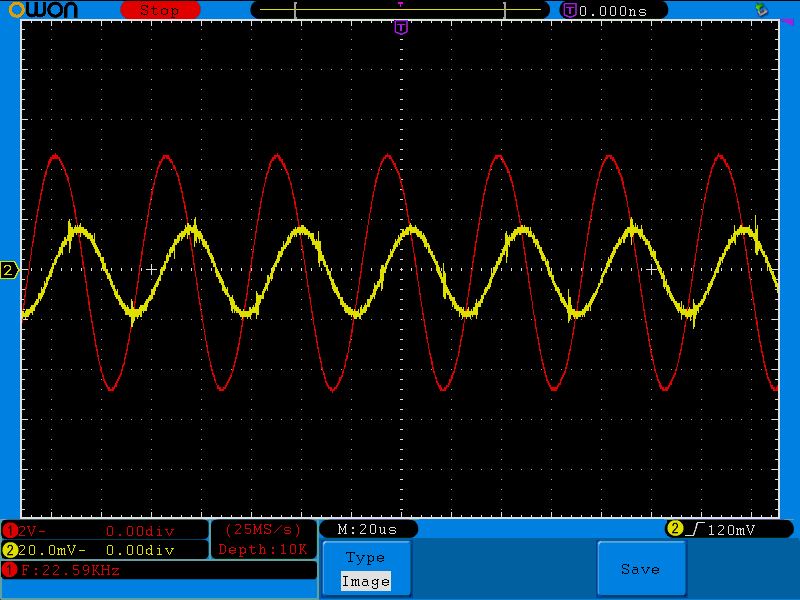
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
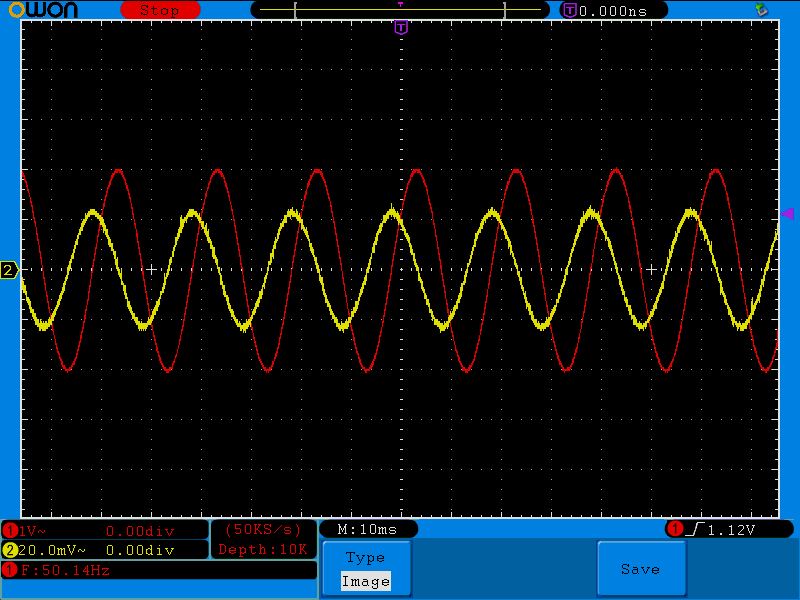
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
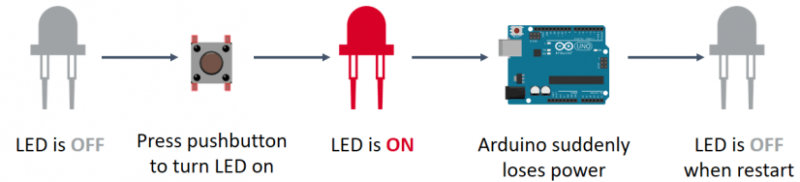
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
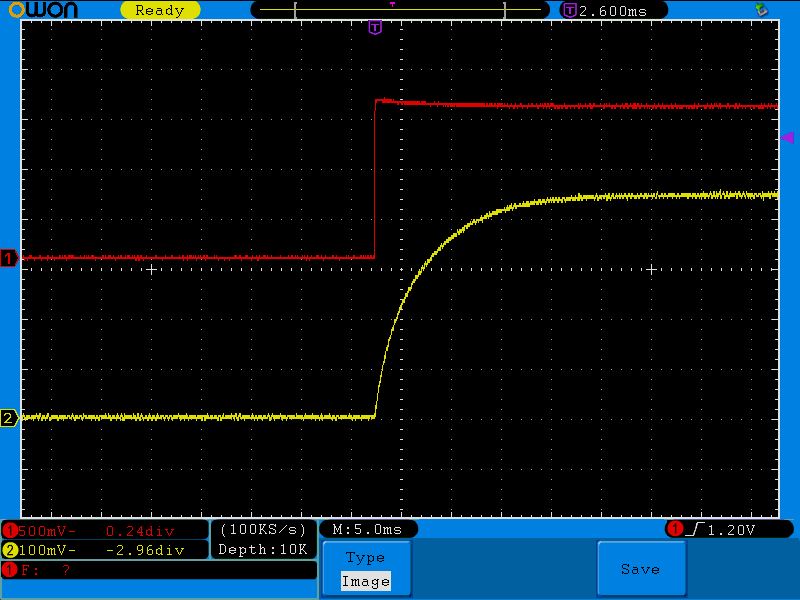
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
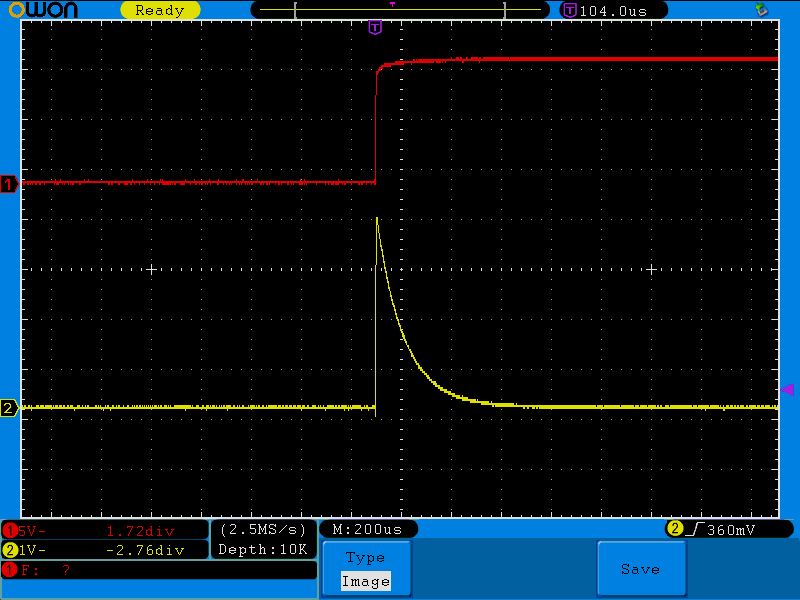
Все с точностью наоборот! Можно даже сказать, что катушка – это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
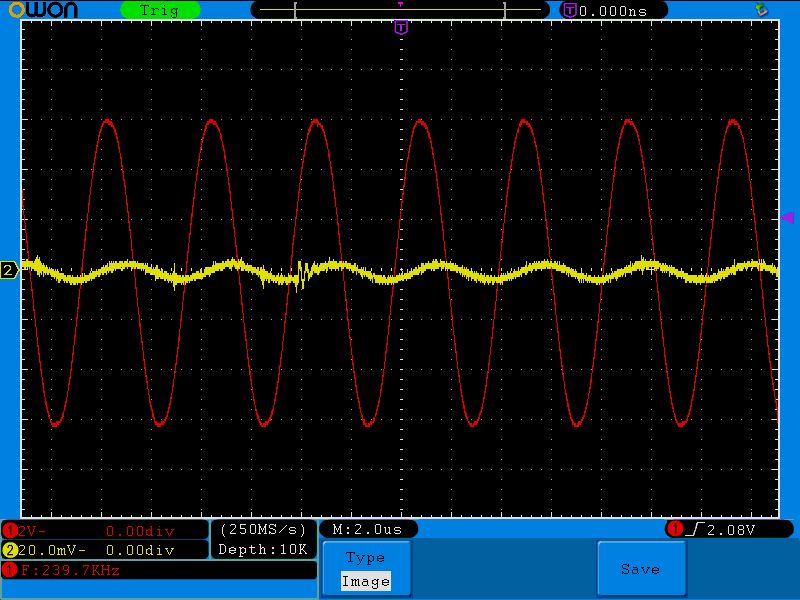
34 Килогерца
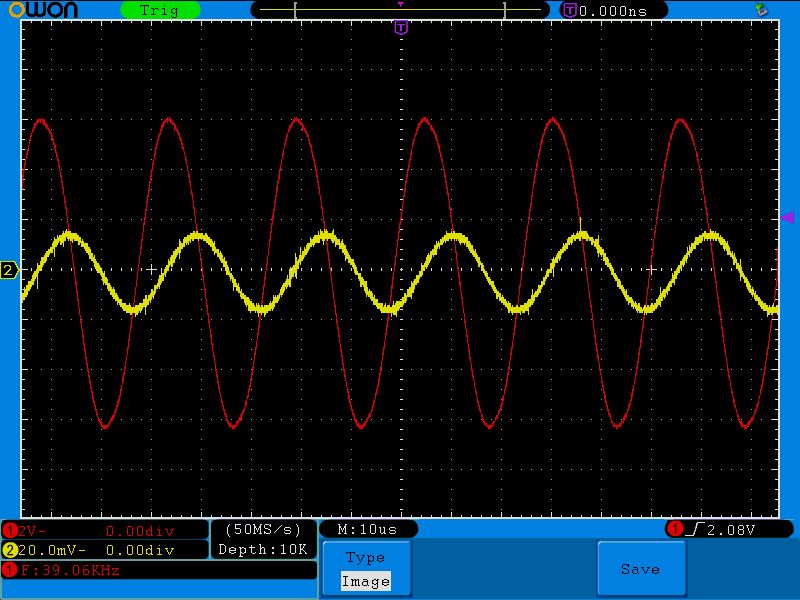
17 Килогерц
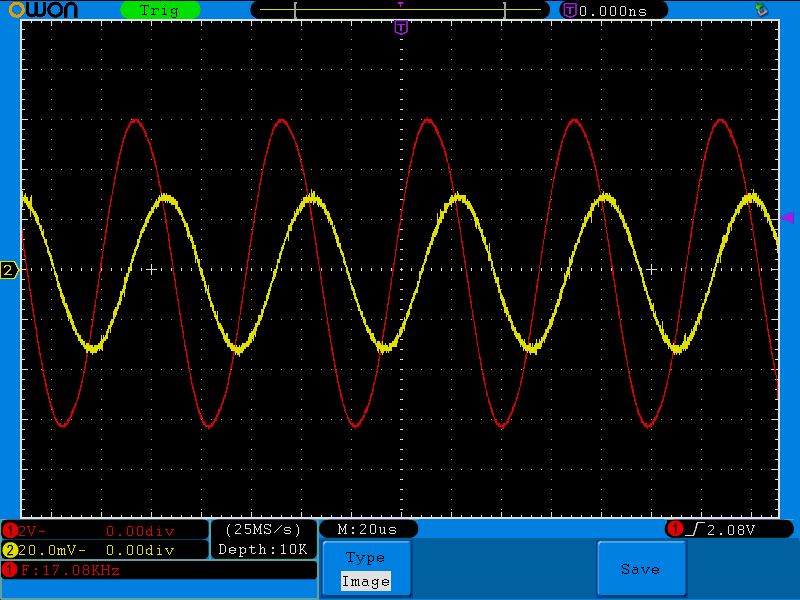
10 Килогерц
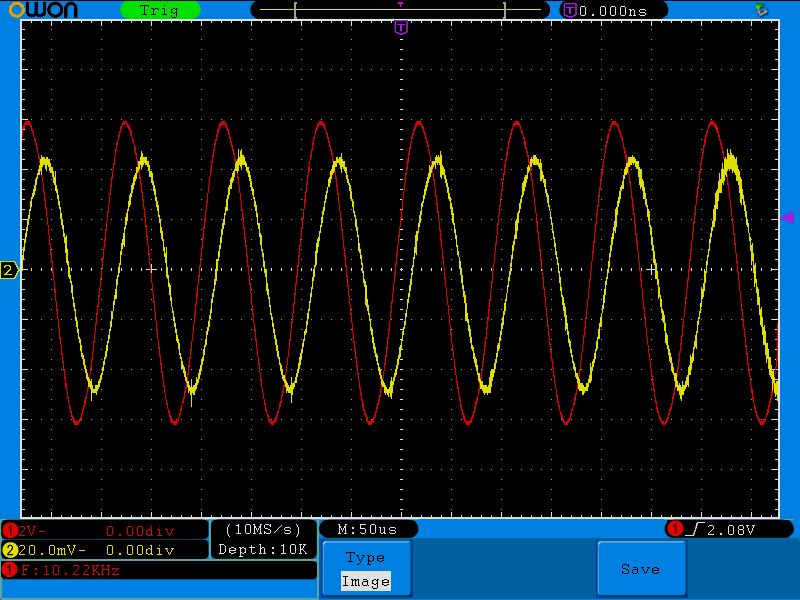
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Индуктивное сопротивление катушки
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением. Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.
Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.
Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.
Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
XL=2π• f •L
где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:
Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.
Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.
Источник
Индуктивное сопротивление катушки
Сопротивление тока: формула
Катушка индуктивности – пассивный компонент электросхем, который имеет возможность сохранять электроэнергию посредством превращения ее в магнитное поле. Такой процесс является главной функцией такого электрического компонента.
Разновидности обозначения катушек индуктивности на электросхемах
По своим свойствам и основным техническим характеристикам индуктивная катушка напоминает конденсатор, какой преобразует энергию в электрополе.
Индуктивность заключается в том, что вокруг проводникового элемента с током образуется магнитное поле. Связано это с ЭДС, что противодействует силе тока и приложенному электронапряжению в катушке. Это свойство есть индуктивное сопротивление катушки. Ее индуктивность можно увеличить посредством увеличения количества витков в ней.
Внешний вид сверхмощной катушки индуктивности
Интересно знать. Согласно закону Ома, сила электротока обратно пропорциональна сопротивлению и прямо пропорциональна электронапряжению в цепи. Если принять сопротивление катушки току переменного типа за величину ωL, то получится закон Ома для электрической цепи с чистой индуктивной нагрузкой. Формула будет выглядеть так: U0=I0*ωL.
Для выяснения количественной характеристики индуктивного сопротивления катушки стоит помнить, что оно противодействует электротоку переменного типа. На практике же индуктивная катушка имеет свое собственное некоторое сопротивление.
Переменный синусоидальный электроток, проходящий через катушку, приводит к возникновению ЭДС, или синусоидального электронапряжения переменного типа
Зная такое важное понятие, как индуктивное сопротивление, а также формулы и зависимости этой величины, можно производить верные расчеты во многих отраслях промышленности, электротехнике и энергетике
Треугольник сопротивлений
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.Активное сопротивление в цепи переменного тока.Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т.
е. имеют место явления индуктивности. Ток возникает под действием электрического поля на заряды, следовательно, проводник должен обладать емкостью, так как в диэлектрической среде вокруг него возникает поток смещения.Однако в ряде случаев относительная роль двух из трех параметров R, L, С в электрической цепи практически незначительна.
Это позволяет рассматривать подобную цепь как обладающую только сопротивлением, или только индуктивностью, или только емкостью.Мы рассмотрим поочередно условия в трех таких простейших цепях переменного тока.В цепи, содержащей только сопротивление г, синусоидальное напряжени u = Um sin ?t источника электроэнергии создает ток:i = u : r = (Um: r ) sin ?tТак как сопротивление r от времени не зависит, то в этой цепи ток совпадает по фазе с напряжением (рис. 1) и изменяется также синусоидально:i = Imsin ?tздесь:Im= Um: rРисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.Разделив последнее выражение на , получим формулу закона Омадля действующих значений напряжения и тока:I = U : rКак видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.
Сопротивление для постоянного тока называют омическим, чтобы отличить его от активного сопротивления для переменного тока.Различие между активным и омическим сопротивлениями обуславливается рядом причин. Одна из них – поверхностный эффект, частичное вытеснение переменного тока в поверхностные слои проводника.Чем больше частота переменного тока, тем это вытеснение значительнее. Из-за поверхностного эффекта сопротивлениеrоказывается уже существенно большим, чем вычисленное по формуле:r = ?
(l : S)Поверхностный эффект создается тем, что переменное магнитное поле индуктирует во внешних слоях проводника меньшую ЭДС самоиндукции, чем во внутренней его части.Особенно сильно поверхностный эффект увеличивает активное сопротивление стальных проводов. На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв. мм).Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.Поделитесь полезной статьей:
https://youtube.com/watch?v=NSxgxMNG2fwrel%3D0%26amp%3Bcontrols%3D0%26amp%3Bshowinfo%3D0
- electrosam.ru
- electrono.ru
- electroandi.ru
- fazaa.ru
Компенсация реактивной мощности
С помощью электрических сетей осуществляется передача электроэнергии на значительные расстояния. В большинстве случаев она используется для питания электродвигателей, имеющих высокое индуктивное сопротивление и большое количество резистивных элементов. К потребителям поступает полная мощность, которая делится на активную и реактивную. В первом случае с помощью активной мощности совершается полезная работа, а во втором – происходит нагрев трансформаторных обмоток и электродвигателей.
Под действием реактивной составляющей, возникающей на индуктивных сопротивлениях, существенно понижается качество электроэнергии. Противостоять ее вредному воздействию помогает комплекс мероприятий по компенсации с использованием конденсаторных батарей. За счет емкостного сопротивления удается понизить косинус угла φ.
Компенсирующие устройства применяются на подстанциях, от которых электричество поступает к проблемным потребителям. Этот способ дает положительные результаты не только в промышленности, но и на бытовых объектах, снижая нагрузку на оборудование.
Активное и реактивное сопротивление — сопротивлением в электротехнике называется величина, которая характеризует противодействие части цепи электрическому току. Это сопротивление образовано путем изменения электрической энергии в другие типы энергии. В сетях переменного тока имеется необратимое изменение энергии и передача энергии между участниками электрической цепи.
При необратимом изменении электроэнергии компонента цепи в другие типы энергии, сопротивление элемента является активным. При осуществлении обменного процесса электроэнергией между компонентом цепи и источником, то сопротивление реактивное.
В электрической плите электроэнергия необратимо преобразуется в тепло, вследствие этого электроплита имеет активное сопротивление, так же как и элементы, преобразующие электричество в свет, механическое движение и т.д.
В индуктивной обмотке переменный ток образует магнитное поле. Под воздействием переменного тока в обмотке образуется ЭДС самоиндукции, которая направлена навстречу току при его увеличении, и по ходу тока при его уменьшении. Поэтому, ЭДС оказывает противоположное действие изменению тока, создавая индуктивное сопротивление катушки.
С помощью ЭДС самоиндукции осуществляется возвращение энергии магнитного поля обмотки в электрическую цепь. В итоге обмотка индуктивности и источник питания производят обмен энергией. Это можно сравнить с маятником, который при колебаниях преобразует потенциальную и кинетическую энергию. Отсюда следует, что сопротивление индуктивной катушки имеет реактивное сопротивление.
Самоиндукция не образуется в цепи постоянного тока, и индуктивное сопротивление отсутствует. В цепи емкости и источника переменного тока изменяется заряд, значит между емкостью и источником тока протекает переменный ток. При полном заряде конденсатора его энергия наибольшая.
В цепи напряжение емкости создает противодействие течению тока своим сопротивлением, и называется реактивным. Между конденсатором и источником происходит обмен энергией.
После полной зарядки емкости постоянным током напряжение его поля выравнивает напряжение источника, поэтому ток равен нулю.
Конденсатор и катушка в цепи переменного тока работают некоторое время в качестве потребителя энергии, когда накапливают заряд. И также работают в качестве генератора при возвращении энергии обратно в цепь.
Активное и реактивное сопротивление
Реактивная составляющая встречается в двух формах: емкостной (она присуща конденсаторным устройством) и индуктивной (свойственна трансформаторам, катушкам и обмоткам). Для определения отношения между напряжением и токовой силой требуется знать показатели всех видов оказываемого проводником сопротивления.
Реактивное сопротивление
Когда конденсатор подсоединен в электроцепь, за временной период до смены полярности он успевает набрать только некоторый процент заряда. Частота тока прямо пропорциональна величине заряда, набираемой элементом. Реактивный эффект на конденсаторном элементе наблюдается из-за того, что у него есть емкость. Когда частота возрастает, емкостное противодействие падает. Благодаря этому эффекту, данные детали хорошо подходят для использования в роли шунта с меняющейся величиной.
У катушки при увеличении токовой частоты растет и индуктивное противодействие. Помимо частоты, на значение также сильно влияет обмоточная индуктивность.
Важно! Бывает, что результирующая реактивная составляющая в цепи с несколькими обмотками и конденсаторами оказывается равной нулю. В таком случае фазы напряжения и электротока совпадают
Если между ними есть хоть какая-то разница фаз в ту или другую сторону, реактивная компонента будет отличной от нуля.
В реальности детали электрической цепи имеют как активную, так и обе реактивных составляющих. Но в ряде случаев одной или двумя из них принято пренебрегать из-за очень малых показателей, незначительно влияющих на общую ситуацию в сети. К примеру, обычно принимают, что конденсатор (если пренебречь энергетическими потерями) имеет исключительно емкостное противодействие
У лампочек накаливания, в свою очередь, принимается во внимание только активная компонента. У обмоточных элементов выделяются активная и индуктивная составляющие
Реактивное индуктивное и емкостное
Выше рассказывалось о скин-эффекте, имеющем место в прямом проводнике. Если проводник смотан в катушку (обмотку), протекающий по нему переменный ток создает более сильное переменное магнитное поле, и наводимая им ЭДС самоиндукции не просто вытесняет ток во внешние слои проводника, а ощутимо ему противодействует. Такое противодействие катушки называют индуктивным сопротивлением.
Индуктивное сопротивление
Вычисляется индуктивное сопротивление по формуле XL = 2П * f * L, где
- f — частота переменного тока, Гц;
- L — индуктивность катушки, Гн.
Таким образом, чем выше f, тем больше XL. Этим свойством катушки пользуются при фильтрации высокочастотных помех (гармоник) в сети.
Свойства XL, отличающие его от R:
- ток в цепи отстает по фазе от напряжения на 900;
- превращение электроэнергии является обратимым: сначала она преобразуется в магнитное поле (1-я половина полупериода), затем накопленная в нем энергия снова становится электрической (вторая половина).
Обмотки применяются в электромоторах и трансформаторах, потому потребители с такими компонентами имеют значительное индуктивное сопротивление. На его преодоление тратится часть мощности электротока, именуемая реактивной Wр. В противоположность ей, другую часть, совершающую полезную работу, называют активной Wа.
Коэффициент мощности
При сложении обеих составляющих графическим путем, получается треугольник (прямоугольный), в котором полная мощность Wп является гипотенузой. Если угол между ней и вектором активной мощности Wа обозначить через ϕ, то: cosϕ = Wа / Wп.
Для каждого устройства с индуктивным сопротивлением cosϕ обозначается в характеристиках. Также приводится активная мощность, причем выходная, например, на валу электродвигателя. Таким образом, чтобы определить полную потребляемую мощность устройства, следует сделать действие: Wп = Wа / (cosϕ * КПД), где КПД — коэффициент полезного действия прибора.
Необходимость преодолевать реактивное сопротивление, создает значительную дополнительную нагрузку на энергогенерирующее оборудование электростанций. Чтобы разгрузить его, в электросетях применяют установки компенсации реактивной мощности. Они представляют собой конденсаторные батареи.
Емкостным сопротивлением обладают конденсаторы. В цепи постоянного тока этот элемент ток не пропускает, но переменный течет через него относительно свободно, поскольку емкость имеет свойство накапливать в себе заряд.
В 1-й четверти периода она заряжается, во второй — разряжается, в 3-й и 4-й — действия повторяются, но уже с обратной полярностью. При этом он работает подобно индукционной катушке: в 1-й половине полупериода накапливает часть энергии электрогенератора, во 2-й — возвращает ее в цепь.
То есть конденсатор тоже противостоит преобразованию переменного тока — в этом состоит суть емкостного сопротивления. Вычисляют емкостное сопротивление по формуле: Xc = 1 / (2П * f * C), где С — емкость конденсатора, Ф (фарад).
За счет разрядки элемента, ток в цепи опережает напряжение по фазе на 900. На преодоление емкостного сопротивления также расходуется часть полной мощности — реактивная. Установки для ее компенсации содержат индукционные катушки.
Мощность в цепи с реактивными радиоэлементами
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность – это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком “плюс”, а напряжение со знаком “минус”. В итоге плюс на минус дает минус. Получается мощность со знаком “минус”. А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем “плющить” пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно – это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо – это уже другая история.
В третий промежуток времени t3 и ток и напряжение у нас со знаком “минус”. Минус на минус – это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL – это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L – собственно сама индуктивность катушки
С – межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r – сопротивление диэлектрика и корпуса между обкладками
С – собственно сама емкость конденсатора
ESI (ESL) – эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
§ 2.9. Закон Ома для электрической цепи переменного тока
Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С (рис. 2.20).
Рис. 2.20
Чему равна амплитуда силы тока в такой цепи (колебательном контуре), если на ее концах поддерживается напряжение u(t) = U sin ωt?
Мы видели, что при включении по отдельности в цепь проводника с активным сопротивлением R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами (2.6.2), (2.7.3) и (2.8.4). Амплитуды же напряжений на резисторе, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так:
В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи переменного тока, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.
Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.
Действительно, квазистационарный ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлением. Однако только на участке с активным сопротивлением колебания напряжения и силы тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний силы тока на π/2 (см. § 2.7), а на катушке индуктивности колебания напряжения опережают колебания силы тока на π/2 (см. § 2.8).
Векторная диаграмма электрической цепи
Для вывода закона Ома в случае электрической цепи переменного тока, изображенной на рисунке 2.20, нужно уметь складывать мгновенные колебания напряжений, сдвинутых по фазе друг относительно друга. Проще всего выполнять сложение нескольких гармонических колебаний с помощью векторных диаграмм, о которых было рассказано в § 1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду силы тока в зависимости от амплитуды напряжения и сдвиг фаз между силой тока и напряжением.
Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока m. Этот вектор изобразим в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с силой тока. Поэтому вектор mR должен совпадать по направлению с вектором m. Его модуль равен UmR = ImR.
Рис. 2.21
Колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2 и соответствующий вектор и mL должен быть повернут относительно вектора m на π/2. Его модуль равен UmL = IωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор mL следует повернуть налево на π/2. (Можно было бы, конечно, поступить и наоборот.)
Вектор напряжения на конденсаторе mC отстает по фазе от вектора m на π/2 и поэтому повернут на этот угол относительно вектора m направо. Его модуль равен .
Для нахождения вектора суммарного напряжения m нужно сложить три вектора: mR, mL и mC. Вначале удобнее сложить два вектора mL и mC (рис. 2.22).
Рис. 2.22
Модуль этой суммы равен , если . Именно такой случай изображен на рисунке. После этого, сложив вектор mL + mC с вектором mR, получим вектор m, характеризующий колебания напряжения в сети.
По теореме Пифагора (из треугольника АОВ):
или
Из равенства (2.9.2) можно найти амплитуду силы тока в цепи:
Это и есть закон Ома для электрической цепи переменного тока, изображенной на рисунке 2.20.
Благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи (см. рис. 2.20) выражается так:
От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин. Они связаны друг с другом точно так же, как и амплитуды в формуле (2.9.3):
Мгновенное значение силы тока меняется со временем гармонически:
где φc, — разность фаз между силой тока и напряжением в сети. Она зависит от частоты со и параметров цепи R, L, С.
Сдвиг фаз между током и напряжением
Сдвиг фаз φc, между колебаниями силы тока и напряжения равен по модулю углу φ между векторами m и m (см. рис. 2.22). Как следует из этого рисунка,
Согласно рисунку 2.22, сила тока отстает от напряжения по фазе при условии . Поэтому сдвиг фаз φc = -φ и
В частных случаях цепей с активным, емкостным и индуктивным сопротивлениями из этой формулы получаются правильные значения сдвига фаз.
Активное сопротивление в цепи переменного тока
Определим величину тока в цепи переменного тока с чисто активным сопротивлением.
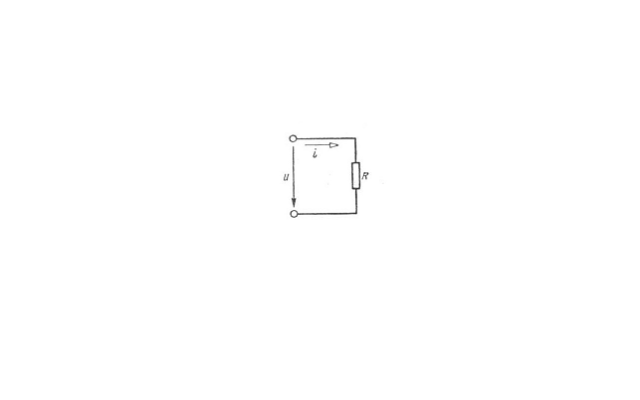
Рис. 3. Схема с чисто активной нагрузкой.
Для переменного тока закон, по которому меняется мгновенное значение напряжения, имеет следующий вид:
$$U=U_m sin(\omega t+\varphi)$$
Мгновенное значение тока через любой элемент находится по закону Ома:
$$I ={U \over R}$$
Подставляя предыдущую формулу в закон Ома, получим:
$$I={U_m sin(\omega t+\varphi)\over R}=I_m sin(\omega t+\varphi)$$
Из этой формулы видно, что колебания силы тока в цепи с чисто активным сопротивлением имеют ту же частоту и фазу, что и колебания напряжения. Ток в цепи в любой момент времени возрастает пропорционально напряжению. Амплитуда активного сопротивления постоянна. А значит, действующие значения переменного напряжения и тока также можно находить по закону Ома.
Это важная особенность активного сопротивления. Оно не обладает инерционностью, ток и напряжение через него изменяются синфазно. Вся энергия движущихся по активному сопротивлению зарядов сразу преобразуется в тепловую (и, возможно, механическую).
Отсюда следует, что энергия, выделяемая на активном сопротивлении в цепи переменного тока, находится непосредственно из закона Джоуля-Ленца с использованием действующих значений:
$$А = I^2Rt$$
Указанные соотношения справедливы только для чисто активных сопротивлений. Для сопротивлений, которые имеют реактивную составляющую, к примеру, для катушки индуктивности, зависимость мгновенного значения тока сложнее, и закон Джоуля-Ленца в таком виде использовать нельзя.
Любой реальный проводник обладает некоторой индуктивностью, а между любыми частями реальных проводников и элементов существует некоторая электроемкость. Поэтому чисто активных сопротивлений, строго говоря, не существует. Любое реальное активное сопротивление имеет некоторую реактивную составляющую. На низких частотах она очень мала, и ею пренебрегают. На высоких же частотах ею пренебречь нельзя, и она всегда оказывает заметное влияние на поведение и параметры цепи.
Что мы узнали?
Сопротивление, на котором энергия электрического тока выделяется в виде тепла, называется активным. Оно не обладает инерционностью. Ток, протекающий через активное сопротивление, синфазен с напряжением на нем, и его можно найти по закону Ома для действующих значений. Мощность, выделяемая на активном сопротивлении, можно найти по закону Джоуля-Ленца для действующих значений.
Тест по теме
-
Вопрос 1 из 10
Направленное движение зарядов по проводнику называется:
- переменным электрическим током
- постоянным электрическим током
- активным сопротивлением
- реактивным сопротивлением
Начать тест(новая вкладка)